모델을 학습시키는 과정에서 사용되는 손실함수 중 함수의 기울기를 활용하는 경사법을 보다 잘 이해하기 위한 장이다.
1. 미분
미분은 한 순간의 변화량(어느 순간의 속도)이며, 수식으로는 다음과 같이 표현된다:

이를 파이썬으로 구현하면 다음과 같다:
def numerical_diff(f, x):
h = 10e-50
return (f(x+h) - f(x)) / h
그러나 이 코드는 두 가지 오류가 있다.
첫째, 반올림 오차 문제를 일으킨다. h 값이 너무 작아지면 컴퓨터로 계산하는 데 문제가 된다. 따라서 h 값을 10**(-4)로 적절히 수정해본다.
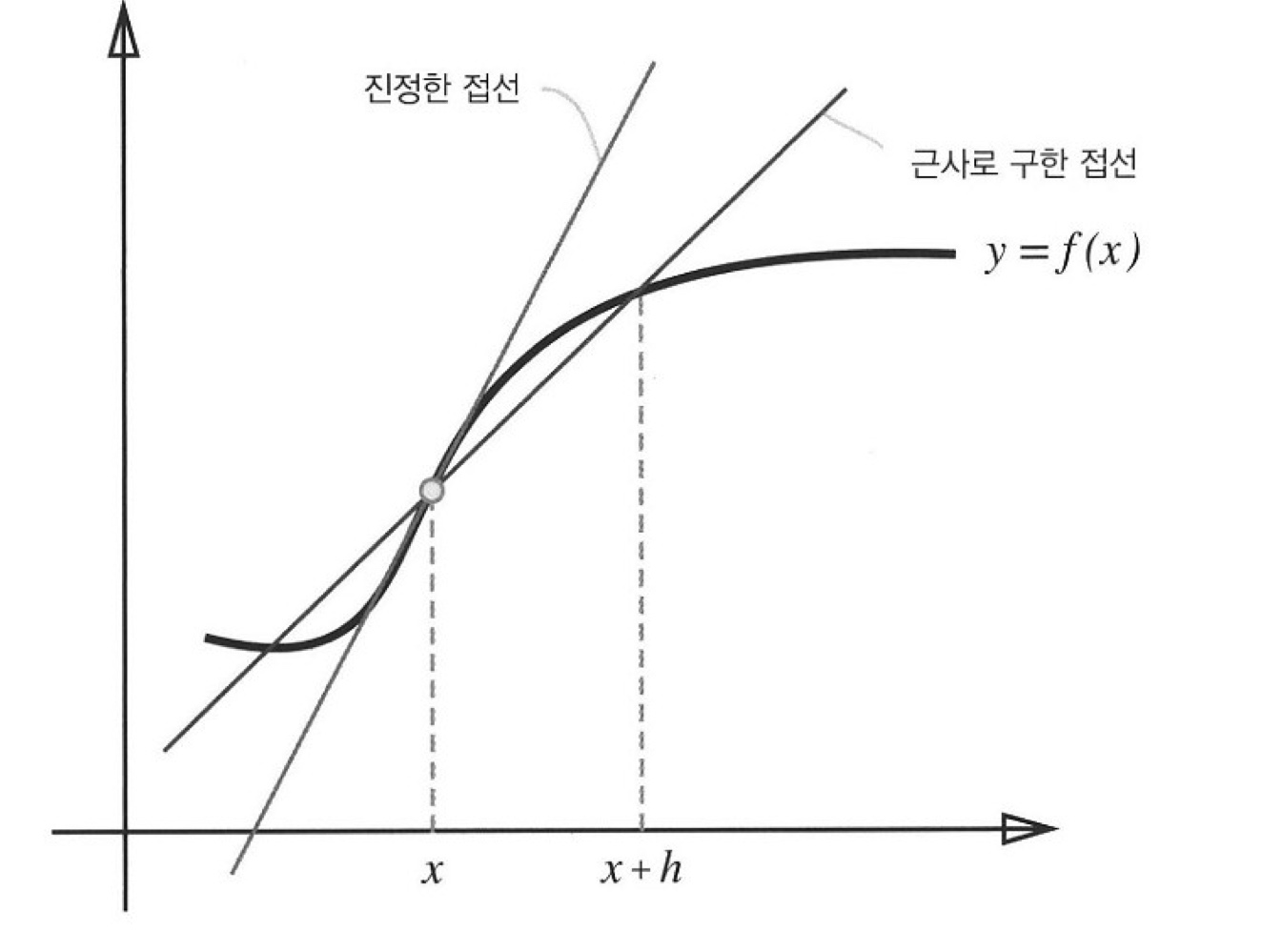
둘째, 위 코드에서는 (x + h)와 x 사이의 기울기를 구현하고 있지만, 이는 엄밀히 진정한 접선과 일치하지 않는다. 이는 h를 무한히 0으로 좁히는 것이 불가능해 생기는 한계이다. 아래 그림에서도 진정한 미분(진정한 접선)과 수치 미분(근사로 구한 접선)의 값이 다르다는 것을 알 수 있다. 이 오차를 줄이기 위해서는 (x + h)와 (x - h)일 때 f의 차분을 계산한다. 이는 중심 차분 혹은 중앙 차분이라고 하며, 기존 (x + h)와 x 사이의 차분은 전방 차분이라고 한다.
수치 미분 코드를 수정한 결과는 다음과 같다:
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
2. 수치 미분의 예
수치 미분을 사용하여 다음 함수를 미분해보자.
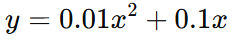
함수를 파이썬으로 구현하면 다음과 같다.
def function_1(x):
return 0.01*x**2 + 0.1*x
함수를 그리면 다음과 같다.

x = 5, x = 10 일 때 함수의 미분을 진행하면 다음과 같이 기울기 값이 큰 오차 없이 도출된다.
>>> numerical_diff(function_1, 5)
0.1999999999990898
>>> numerical_diff(function_1, 10)
0.2999999999986347
두 점에 대한 접선을 그래프로 나타내면 다음과 같다.

3. 편미분
변수가 두 개 이상인 경우에는 편미분을 한다.
예를 들어 다음과 같은 함수가 있다고 하자.
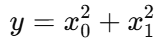
이 식을 파이썬으로 구현하면 다음과 같다.
def function_2(x):
return x[0]**2 + x[1]**2
# 또는 return np.sum(x**2)
함수를 그리면 다음과 같다.
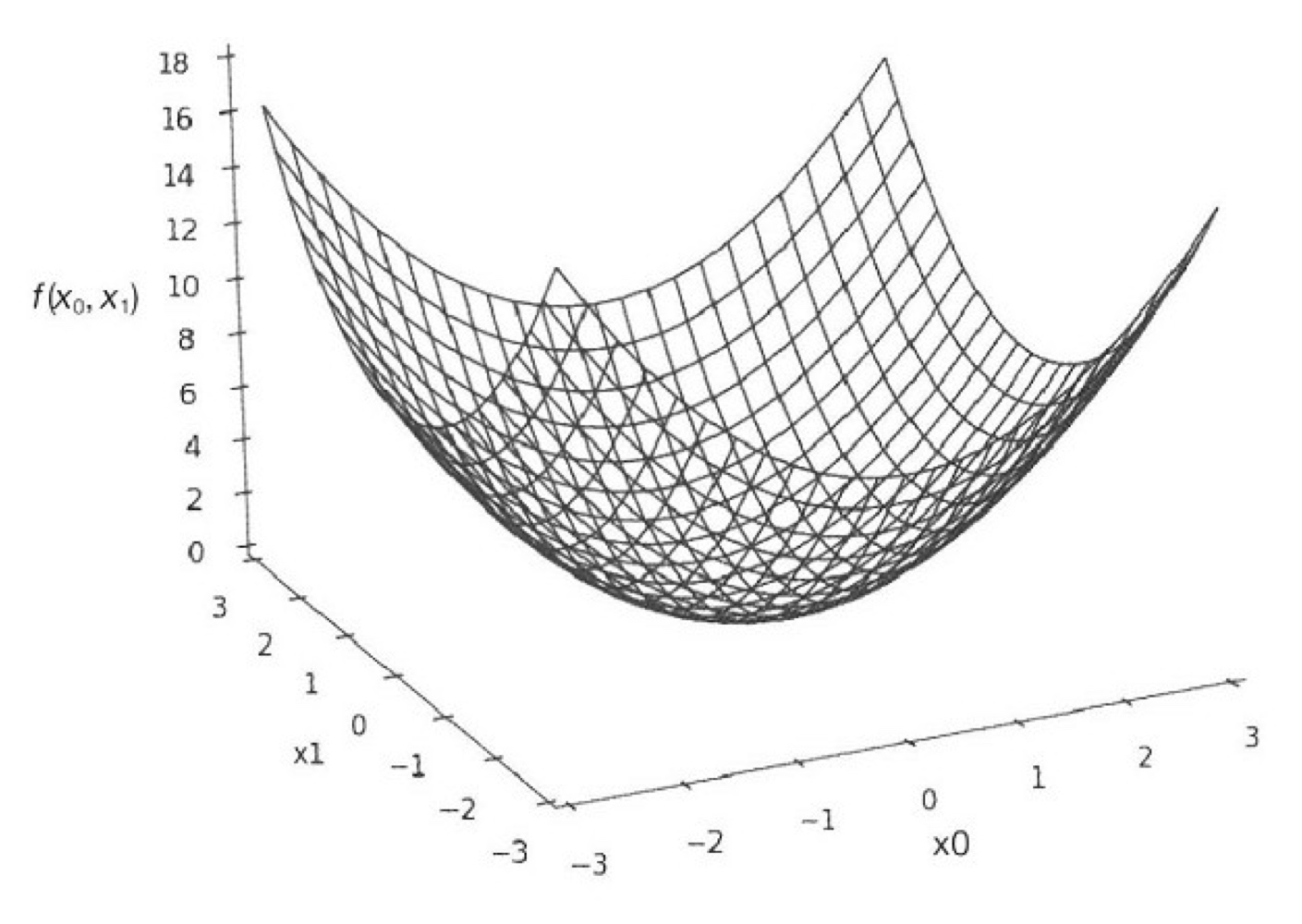
x0 = 3, x1 = 4일 때 x0, x1에 대한 편미분은 각각 다음과 같이 진행된다.
>>> def function_tmp1(x0):
return x0*x0 + 4.0**2.0
>>> numerical_diff(function_tmp1, 3.0)
6.00000000000378>>> def function_tmp2(x1):
return 3.0*2.0 + x1*x1
>>> numerical_diff(function_tmp1, 4.0)
7.999999999999119즉 x0에 대해 편미분을 진행할 때는 x1 = 4를 고정된 값으로 새로운 함수를 임시로 설정한 후, 이를 미분한다. x1에 대한 편미분도 같은 방법으로 진행된다.
편미분은 변수가 하나일 때의 미분과 마찬가지로 특정 장소의 기울기를 구한다.
4. 퀴즈
문제1. 다음 중 수치미분의 오차를 줄이는 방법에 대해 옳은 것은?
1. h 값은 0으로 무한히 작아진다.
2. h 값이 작을수록 오차가 줄어든다.
3. h 값이 클수록 오차가 줄어든다.
4. h 값의 속성으로 인해서 중앙 차분을 활용한다.
문제2. x=2, y=3일 때 다음 함수를 x에 대해 편미분한 값은?

'Miscellaneous' 카테고리의 다른 글
| [2025-1] 박제우 - TabNet : Attentive Interpretable Tabular Learning (0) | 2025.03.15 |
|---|---|
| [2025-1] 임준수 - 밑바닥부터 시작하는 딥러닝 리뷰, (CH 4.2) 손실함수 (0) | 2025.03.12 |
| [2025-1] 박경태 - 밑바닥부터 시작하는 딥러닝(CH 4.5): 학습 알고리즘 구현하기 (0) | 2025.03.12 |
| [2025-1] 노하림 - Beyond Scalar Reward Model: Learning Generative Judge from Preference Data (6) | 2025.03.10 |
| [2025-1] 주서영 - Deep Reinforcement Learning from Human Preferences (0) | 2025.03.06 |



