https://arxiv.org/pdf/2310.04378
[2025-1] Latent Consistency Models : Synthesizing High-Resolution ImagesWith Few-Step Inference
논문 링크: 2310.04378 참고 논문 리뷰 블로그 링크: Latent Consistency Models : Synthesizing High-Resolution ImagesWith Few-Step Inference 논문 리뷰 :: LOEWEN Latent Consistency Models : Synthesizing High-Resolution ImagesWith Few-St
blog.outta.ai
Summary
- Stable Diffusion과 같은 Latent Diffusion Model은 고해상도 text-to-image 합성에서 탁월한 성능을 보이나, 반복적인 reverse process로 생성 속도가 느리다는 단점을 가짐.
- 이를 해결하기 위해 Latent space에 Consistency model을 적용하여 고해상도의 이미지를 적은 단계로 생성하는 모델인 LCM(Latent Consistency Model)을 설계함
- Diffusion models : Reverse function과 ODE를 이용한 이미지 생성 모델
- Consistency model : few-step 혹은 one-step으로 빠르게 sampling
- Latent space : High-resolution image 생성 모델
- One-stage guided distillation : text-to-image와 같이 conditional diffusion model 구현
- Skipping Time Step : 학습 step을 단축하여 training convergence 속도 증가
- Fine-tuning : Customized data에 대해 효율적인 모델 적용
- Result : 기존 모델보다 더 나은 성능, 시간 및 메모리 단축
※ 본 글은 LCM의 Method에 관련하여 더 자세하게 서술하였습니다. 논문에 제시된 식과 알고리즘에 중점을 두고 설명할 예정이니, 논문의 전체 흐름을 위해서는 이전 글을 참고하여 주십시오.
1. Diffusion Models

Diffusion model은 원본 이미지 data에 Gaussian noises를 연속적으로 더하여 완전한 노이즈 이미지를 생성한 다음, Reverse denoising 과정을 거쳐오면서 원본 이미지를 생성하는 과정을 학습한다.
- Origin data distribution : $p_{data} (x)$
- Marginal distribution : $q_t(x_t|x_0)=\mathit N(x_t|a(t)x_0, \sigma ^2(t)I)$
($x_t$는 $t$번째 생성 이미지, $a(t)$와 $\sigma (t)$는 noise schedule을 나타내는 함수로, 각각 평균과 표준편차를 의미)
이미지에서 노이즈를 생성하는 Forward process는 Stochastic differential equation (SDE)의 관점에서 서술할 수 있고, 이를 나타내는 식은 다음과 같다.


반대로, 노이즈에서 원본 이미지를 생성하는 Reverse process에서도 SDE를 정의할 수 있다. Reverse-time SDE의 solution을 sampling함으로써 원본 이미지 $x_0$를 구할 수 있다.
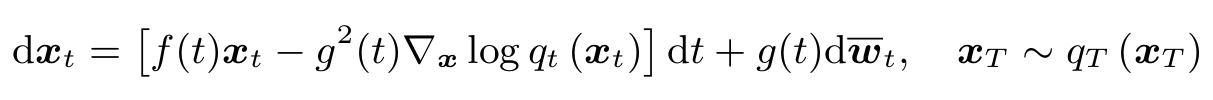
하지만 SDE는 본질적으로 확률론적 효과 $\bar{w_t}$를 포함하기 때문에 직접 soluion을 구하는 것은 복잡하다. 따라서 Probability-flow ODE (PF-ODE)를 새롭게 정의하여 결정론적인 solution을 구하도록 하며, 이 결과는 SDE의 연산 결과인 $q_t(x_t)$와 같은 분포를 가진다고 알려졌다.

ODE (일반 미분방정식) : $\frac{dx}{dt}$와 $f(x,t)$ 간의 관계를 나타내는 방정식. 하나의 해가 도출됨 (결정론적. deterministic)
SDE (확률 미분방정식) : 확률론적 요소가 포함된 ODE. 매번 다른 경로를 가지는 해가 도출됨. (확률론적, stochastic)
PF-ODE (확률 흐름 미분방정식) : Diffusion model의 reverse process SDE에서 확률론적 요소를 제거하여, ODE와 같이 하나의 경로를 가지는 해(결정론적 해)로 변형한 것. SDE의 해와 동일한 결과가 도출되며, 계산량이 적어 빠른 샘플링이 가능하다는 장점이 있다.
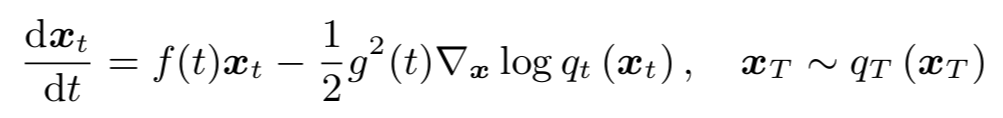
$\epsilon_{\theta} (x_t, t)$는 Noise prediction model로, 원본 이미지에 추가되는 노이즈 값을 예측하는 모델이다. Score function ($-\triangledown \textrm{log} \, q_t(x_t)$)에 fit하도록 설계된다. 이를 예측하는 empirical PF-ODE는 다음과 같다.


결론적으로, Noise prediction model $\epsilon_{\theta}$을 사용한 PF-ODE의 solution을 구함으로써, Diffusion의 reverse process sampling을 할 수 있게 되었다.
2. Consistency Models
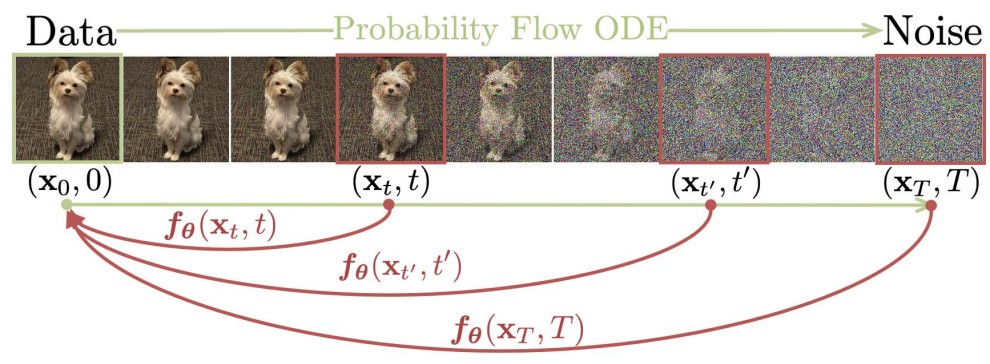
Consistency model은 one-step 혹은 few-step generation을 목표로 설계된 모델로, PF-ODE 경로 내의 어떤 점에서 시작하더라도 그 경로의 origin $x_0$를 바로 구할 수 있게끔 설계된 모델이다.
$f:(x_t, t) \mapsto x_{\epsilon}$


Consistency model을 학습시키기 위해서는 1) Pre-trained diffusion model 내에서 training, 2) scratch training (Isolation) 총 2가지 방법이 있다. 이 중 첫 번째 방법을 Consistency distillation이라고 한다. 이는 기존 Diffusion model에서 생성된 $\left\{x_t\right\}$를 이용하여 PF-ODE 경로를 학습하고, 이 경로 내 모든 $x_t$에 대해 consistency function을 학습하는 것을 뜻한다.

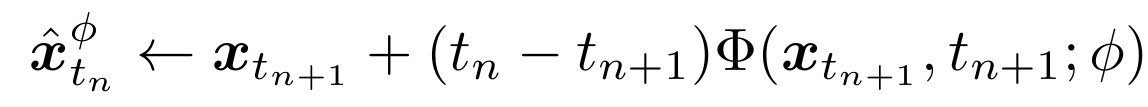
$t_i=(\epsilon^{\frac{1}{\rho}}+\frac{i-1}{N-1}(T^{\frac{1}{\rho}}-\epsilon^{\frac{1}{\rho}}))^{\rho}, \rho=7$
위 식에서 사용된 time schedule $t_n$의 정의이다. $t_n$이 클 때 (초기) 간격이 크고, $t_n$이 작을 때 (후반) 간격이 작다.
ODE solver : 위에 주어진 ODE를 one-step으로 해를 구하는 방정식으로, Pre-trained diffusion model을 기반으로 구한다. 즉, 다음 단계로 sampling하기 위해서 (25)를 $\Phi$로 풀면 diffusion 경로 내에 위치한 $\hat{x_{t_n}}^{\phi}$를 구할 수 있다. Consistency model에서는 랜덤 이미지인 $x_{t_{n+1}}$을 diffusion 경로와 연결짓는 용도로 사용한다.
$\theta ^- \leftarrow \mu \theta ^- + (1-\mu) \theta$
$\theta^-$는 training 중인 model $\theta$의 exponential moving average 값으로 이전 단계까지 수행한 model을 결과값을 반영하여 만들어진 target model이 된다.


3. Latent Consistency Model - Latent Consistency Distillation
Latent space는 LDM의 핵심 원리로, 고해상도 이미지를 Latent space로 가지고 들어올 경우 저해상도 이미지로 변환되어 연산량이 줄어든다는 장점이 있다. LDM은 computation cost를 줄이고 interference process 속도를 증가시켜 high-resolution image를 laptop GPU 수준에서도 생성할 수 있었다.
LCM 역시 고해상도 이미지를 Latent space로 가져와 연산량을 줄일 것이며, 여기에 더해 consistency model을 이용하여 빠른 속도로 이미지를 생성할 수 있도록 설계되었다.
$z=E(x)$, $\hat{x}=D(z)$
Latent space로 통하는 Autoencoder $E$, $D$
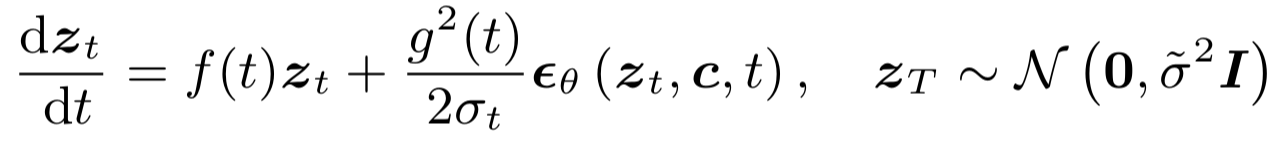

DDIM과 같은 ODE solver $\Psi$를 이용할 경우 PF-ODE를 쉽게 풀 수 있다. 이를 이용해 구한 $\hat{z_{t_n}}^{\Psi}$의 값을 Consistenct distillation loss 식에 적용하고, 그 값을 최소화함으로써 $z_0$로 가는 경로를 구하도록 한다.


이 때 Training, 즉 distillation 과정에서는 $\Psi$를 이용하지만, inference 과정에서는 사용하지 않는다. Inference에서는 학습한 consistency model을 이용하여 $z_0$로 가는 경로를 알 수 있으므로, pre-trained된 Diffusion model이 사용되지 않는다는 것이 특징이다.

LDM과 LCM은 Latent space에서 원본 이미지 생성을 수행하여 고해상도 이미지를 더 적은 연산량으로 복원할 수 있다는 특징을 공유한다. 하지만 Latent space 내에서 DDPM, DDIM 등 diffusion 과정을 학습하는 LDM과 다르게, LCM은 이미 만들어진 Diffusion 모델을 바탕으로 노이즈 이미지에서 원본 이미지를 추출할 수 있는 빠른 경로를 학습하기 때문에 훨씬 빠르게 이미지를 생성한다는 특징이 있다.
DDIM 역시 LCM과 마찬가지로 원본 이미지를 이용하여 Diffusion 중간 단계를 ODE를 이용해 계산하고, step 수를 줄여 이미지 생성 속도를 증가시킨다는 아이디어를 언급하고 있다. 하지만 DDIM은 sampling 과정에서 노이즈 이미지에 ODE를 직접 계산하여 이미지를 생성하지만, LCM의 경우 ODE 경로와 무관하게 원본 이미지를 바로 찾아가는 방법에 대해 학습을 수행하였으므로 sampling 과정에서 ODE 연산없이 단순 모델 적용만으로 이미지를 생성할 수 있다는 차이점이 있다. DDIM은 Diffusion model이지만, LCM은 Diffusion model 경로를 학습하는 Consistency model이다.
4. One-stage guided distillation
Class-conditioned diffusion model에 조건을 적용하기 위하여 Classifier-Free Guidance (CFG)라는 기술이 고안되었다. Classifier Guidance란 모델을 학습하는 과정에서 대입된 조건 $c$를 더욱 잘 반영하도록 유도하는 것을 말한다. 이전에는 classifier로 조건부확률인 $p(y|x_t,\,t)$을 따로 학습하여 conditional model을 구현하였다. 하지만 CFG는 새로운 함수 정의 없이 기존 Noise prediction model인 $e_{\theta}$에 새로운 parameter $w$를 추가하였다. 이 식은 conditional noise와 unconditional noise의 선형 결합으로 표현한다.

Classifier-free guidance는 고해상도의 이미지 생성에 필수적이다. 이전의 방법에서는 two-stage distillation을 사용하였는데, 먼저 $w$를 반영한 $\epsilon_{\theta}$를 학습하고 두 번째 단계에서 Distillation을 수행하여 DDIM 방식으로 sampling step을 줄여나간다. 이는 연산량이 많고, accumlated error가 있다. LCM은 augmented PF-ODE를 적용하여 one-stage guided distillation으로 변경한다. 위의 (8), (11), (10)에 parameter $w$만을 반영한 것과 같다.
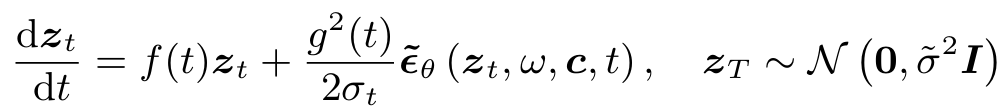


5. Skipping time step
Skipping method는 time-step schedule을 1000여 개에서 수십개로 줄여 수렴속도를 더욱 높이고 모델 성능을 유지하는 방법이다. Consistency model에서 사용하던 $t_{n+1} \rightarrow t_n$ 방식을 $t_{n+k} \rightarrow t_n$ 방식으로 몇 단계를 뛰어넘었다. 논문에서는 $k=20$에서 속도와 정확도의 균형을 맞출 수 있었다고 한다.

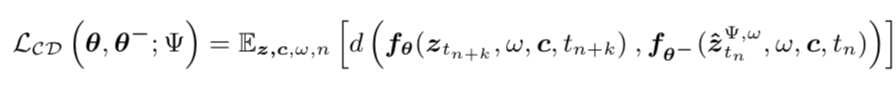
최종적으로, ODE solver로 사용할 수 있는 DDIM, DPM-solver, DPM-solver++를 ODE solver $\Psi$에 적용함으로써 모델이 완성된다. 예시로, DDIM은 아래 식을 적용하였다.


6. Fine-tuning
LCF는 pre-trained된 LCM에 대해 fine-tuning method를 적용한 것이다. Cutomized된 dataset에 맞춰 효율적인 few-step inference를 수행할 수 있다.

Conclusion
- LCM은 다양한 method를 사용한 고해상도 이미지 생성 모델로, 높은 성능과 효율적인 속도를 보였다.
- PF-ODE로 표현한 Diffusion model의 경로를 이용하여, 모든 지점에서 원본 이미지에 수렴하도록 하는 Consistency model을 학습한다. 이 때 Skipping time step을 이용하여 Training 속도를 높이고, Consistency model의 이미지 sampling 방식에 의해 생성 속도도 높였다.
- Latent space는 고해상도의 이미지를 생성하기 적합한 구조이다. 이 외에도 Classifier-Free Guidance를 이용하여 주어진 조건에 맞게 이미지를 생성하며, Fine tuning을 할 경우 customized input data에 맞춰 model이 만들어지므로, 상대적으로 높은 품질의 이미지를 생성할 수 있었다.
참고하면 좋은 논문
Score-Based Generative Modeling through Stochastic Differential Equations [논문] [리뷰]
Elucidating the Design Space of Diffusion-Based Generative Models [논문]
Denoising Diffusion Probabilistic Models [논문] [리뷰]
Denoising Diffusion Implicit Models [논문] [리뷰]
High-Resolution Image Synthesis with Latent Diffusion Models [논문] [리뷰]
Diffusion Models Beat GANs on Image Synthesis [논문] [리뷰]
Classifier-Free Diffusion Guidance [논문] [리뷰]




