DDPM(Denoising Diffusion Probabilistic Models)은 2020년 Jonathan Ho 등이 제안한 모델입니다.
[DDPM]
https://arxiv.org/abs/2006.11239
Denoising Diffusion Probabilistic Models
We present high quality image synthesis results using diffusion probabilistic models, a class of latent variable models inspired by considerations from nonequilibrium thermodynamics. Our best results are obtained by training on a weighted variational bound
arxiv.org
<DDPM 논문 리뷰>
* Abstract
1. 우리는 비평형 열역학(nonequilibrium thermodynamics)에서 영감을 받은 잠재 변수(latent variable) 모델의 한 종류인 확산 확률 모델(diffusion probabilistic models)을 사용하여 고품질 이미지 합성 결과를 제시합니다.
2. 최상의 결과는 확산 확률 모델과 Langevin dynamics 기반의 Denoising Score Matching 간의 새로운 연결을 바탕으로 설계된 가중치가 적용된 변분 하한(weighted variational bound)로 학습함으로써 얻어졌습니다.
3. 또한, 우리의 모델은 점진적 손실 압축(progressive lossy decompression) 방식을 자연스럽게 수용하며, 이는 자기회귀 디코딩(autoregressive decoding)을 일반화한 것으로 해석될 수 있습니다.
4. Unconditional CIFAR10 데이터셋에서 9.46의 Inception score와 3.17의 최고성능 FID score을 획득했습니다. 256x256 LSUN에서는 ProgressiveGAN과 유사한 샘플 품질을 얻었습니다.
* Introduction

1. 확산 확률 모델은 변분 추론(variational inference)을 사용해 학습된 매개변수화된 마르코프 체인(parameterized Markov chain)로, 유한한 시간 후 데이터와 일치하는 샘플을 생성합니다.
2. 이 체인의 전이는 샘플링과 반대 방향으로 데이터를 점진적으로 노이즈화하여 신호를 파괴하는 확산 과정(diffusion process)을 역으로 수행하도록 학습됩니다.
3. 확산이 소량의 가우시안 노이즈로 구성될 때, 샘플링 체인의 전이를 조건부 가우시안(conditional Gaussian)으로 설정하는 것만으로 충분하며, 이를 통해 특히 단순한 신경망 매개변수가 가능해집니다.
- 더 직관적인 이해

* Background
1. Diffusion 모델
- 주변 확률 분포(Marginal probability distribution)

- x_1, ....., x_T: 잠재 변수(latents)
- x_0의 Sampling → p_theta(x_0)를 q(x_0)에 근사시키려 한다.

2. Forward Process
- q(x_1:T | x_0): x_0를 점진적으로 노이즈화하여 순수 가우시안 노이즈 x_T ∼ N(0, I) 로 만드는 과정
- q(x_t: x_t-1): Forward Process에서 x_t가 x_t-1로부터 생성되는 조건부 분포 (조건부 가우시안)
- beta_t: 각 단계에서 추가되는 노이즈의 크기
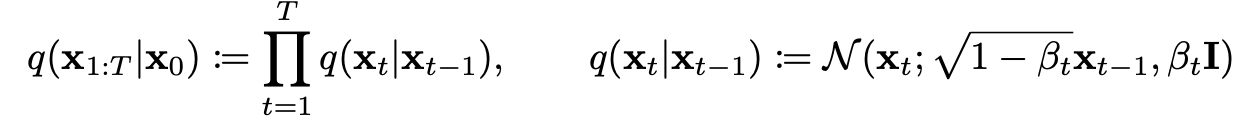
3. Reverse Process
- p_theta(x_0:T): x_T에서 x_0으로 진행하는 모든 단계의 확률을 곱한 것
- q(x_t-1: x_t): Reverse Process에서 x_t-1가 x_t로부터 생성되는 조건부 분포 (조건부 가우시안)
→ 즉, mu_theta와 sigma_theta를 학습시키고자 한다.
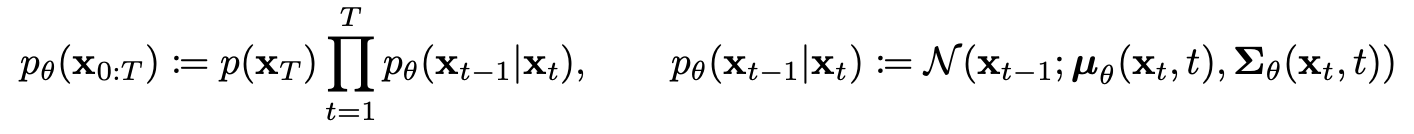
4. Closed Form
- t 시점의 데이터 x_t를 closed form으로 sampling 가능 → 효율적
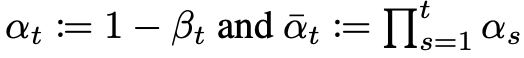
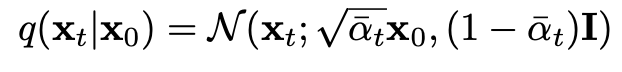
5. Loss - Fundamental
- Negative Log Likelihood
- p_theta(x_0) → 1
- 그러나 계산 복잡 → 변분 하한(ELBO)을 사용하여 최적화

6. Loss - KL Divergence
- KL Divergence: 두 확률분포의 차이를 계산하는 데에 사용하는 함수
- 수학적 테크닉 → Appendix A
- L_T: q(x_T | x_0) 와 p(x_T) 비교
- L_t-1: q(x_t-1 | x_t, x_0) 과 p_theta(x_t-1 | x_t) 비교
- L_0: Reverse Process에서 x1 → x0 복원 확률 평가

- 모든 KL Divergence 가 가우시안 분포 간의 비교 → Rao-Blackwellized fashion을 이용하여 closed form 형태로 계산 가능
* Diffusion models and denoising autoencoders
1. 개요
- Diffusion 모델은 잠재 변수 모델(latent variable model)의 제한된 형태로 보일 수 있지만, 구현에서 상당한 자유도를 허용합니다.
- Forward Process의 분산 β_t, 모델 아키텍처, 그리고 Reverse Process의 가우시안 분포 매개변수(parameterization)를 선택해야 합니다.
- 우리는 Diffusion 모델과 Denoising Score Matching을 명시적으로 연결하는 새로운 방법을 제시하며, 이를 통해 Diffusion 모델에 대해 단순화되고 가중치가 적용된 변분 하한(variational bound) 목표를 도출합니다.
2. Loss component 분석
- L_T: beta_t가 learnable 하지 않고 고정되어 있기 때문에, L_T는 상수
- L_1:T-1: mu 추정 → epsilon 추정

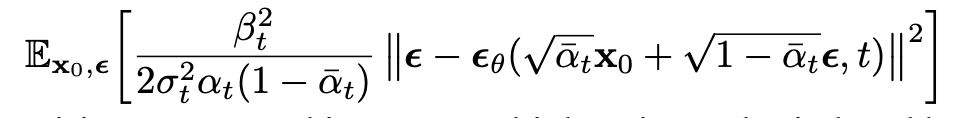
- L_0: 계산 가능
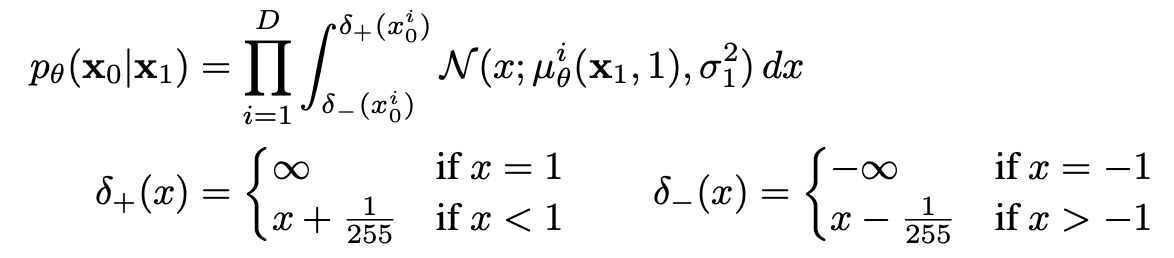
3. Loss - Simplified
- 샘플 품질 개선 및 구현 단순화 → 가중 변분 하한(variational bound)
- t = 1 ~ T 까지 균일하게 sampling
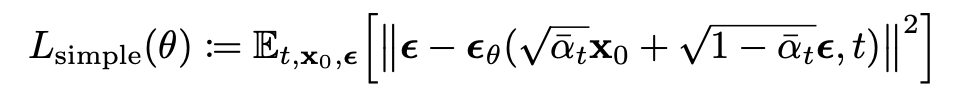
4. Algorithm

* Experiments
1. 개요
- Forward Process에서 beta_T에 linear scheduler 사용 (beta_1 = 10^-4, beta_T = 0.02)
- Reverse Process의 network로 U-Net backbone 사용
- Transformer의 Sinusoidal Position Embedding를 사용하여 t 정보 추가
- 16×16 피처 맵 해상도에서 Self-Attention 사용 → 적당한 크기에서 global relationship 학습
2. Performance

3. Examples






