https://arxiv.org/abs/1512.03385
Deep Residual Learning for Image Recognition
Deeper neural networks are more difficult to train. We present a residual learning framework to ease the training of networks that are substantially deeper than those used previously. We explicitly reformulate the layers as learning residual functions with
arxiv.org
https://arxiv.org/abs/1603.05027
Identity Mappings in Deep Residual Networks
Deep residual networks have emerged as a family of extremely deep architectures showing compelling accuracy and nice convergence behaviors. In this paper, we analyze the propagation formulations behind the residual building blocks, which suggest that the f
arxiv.org
본 포스팅에서는 Deep Residual Learning for Image Recognition 논문을 베이스로, Identity Mappings in Deep Residual Networks의 개념을 추가하여 전반적인 ResNet의 이해를 목표로 한다.
1. Motivation
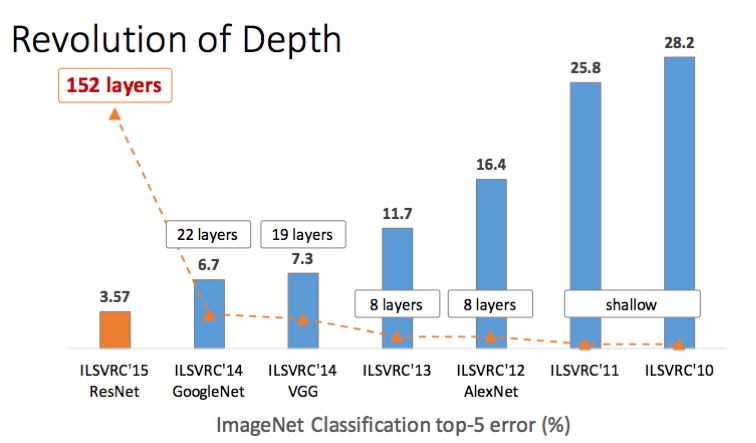
ResNet(Residual Network)은 ResNet(Residual Network)은 2015년 ILSVRC(ImageNet Large Scale Visual Recognition Challenge)에서 우승을 차지한 알고리즘이다. 이 모델은 마이크로소프트의 북경 연구소에서 개발되었다.
ResNet은 152개의 layer로 구성되어, 22개 layer로 구성된 GoogLeNet보다 약 7배 더 깊은 구조를 가진다. 모델의 깊이가 크게 확장되었음에도 낮은 에러율을 기록하며 주목받았다.
저자들은 단순히 네트워크 깊이만 깊어지면 성능이 좋아지는지 확인하고자, 컨볼루션 층과 fully-connected 층으로 구성된 20층 네트워크와 56층 네트워크를 각각 설계하여 비교 실험하였다.

- 실험 결과:
네트워크가 깊어질수록(top-5 error 기준) 성능이 좋아지는 경향이 관찰되었으나, 56층 네트워크는 오히려 20층 네트워크보다 성능이 낮아졌다. 이를 통해 기존 방식으로는 단순히 네트워크를 깊게 만드는 것이 항상 성능 향상을 보장하지 않는다는 점이 확인되었다. - 새로운 접근의 필요성:
ResNet의 저자들은 망의 깊이를 확장하면서도 성능을 유지하거나 개선할 수 있는 새로운 방법이 필요하다는 결론에 도달했다.
20+36 layer로 구성된 네트워크는 Model Capacity가 더 크므로, 적어도 Training 데이터에 한해서는 20 layer로 구성된 네트워크와 비슷하거나 더 나은 성능을 보여아 한다. 만약 Overfitting이 발생하더라도 Training 데이터에서의 성능은 더 높아지는 것이 일반적이지만, 위 실험 결과에서는 Training과 Test 모두 Shallow 네트워크가 더 나은 성능을 보인다. 이는 네트워크가 깊어질수록 최적화가 더 어려워지기 때문이라고 생각할 수 있다. ResNet은 이를 해결하며 152개의 layer를 가진 Deep 네트워크를 성공정으로 훈련시켰다.
2. Residual Block 제안
ResNet의 핵심은 Residual Block이다. 네트워크가 깊어질수록 성능이 저하되는 문제를 해결하기 위해 Residual Block을 제안하였다.
Residual Block은 기존의 네트워크 구조에 간단한 지름길(shortcut)을 추가하는 방식으로 설계되었으며, 이를 통해 학습 과정에서 최적화를 용이하게 한다.

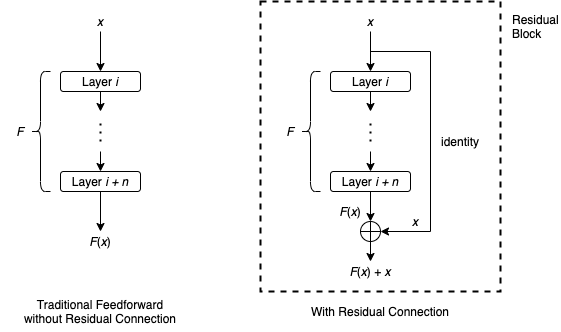
Residual Block의 핵심은 입력값 \(x\)를 그대로 출력값에 더해주는 Skip-Connection(Shortcut)을 도입하는 것이다. 이를 통해 각 층은 기존에 학습된 정보를 유지하면서 추가적인 정보만 학습할 수 있다.
- 구조
- 출력값 \(y\)는 \( y = f(x) \)로 정의된다.
- \( f(x) \)는 입력 \(x\)를 변환한 결과이며, 주로 Convolution, Batch Normalization, ReLU와 같은 연산으로 구성된다.
- 입력 \(x\)는 Skip-Connection을 통해 \( f(x) \)와 더해진다.
- 특징
- 기존의 입력값 \(x\)를 그대로 보존하여 정보 손실을 방지한다.
- 각 층이 학습해야 할 매핑은 \( f(x) = y - x \) 로 단순화된다. 이는 입력값 \(x\)와 출력값 \(y\)간의 차이(잔여 정보)를 학습하는 것이다.
- Skip-Connection 덕분에 깊은 네트워크에서도 기울기 소실 문제(vanishing gradient)가 완화된다.
Plane Layer(기존 방식)
- 입력값 \(x\)를 새로운 값으로 변환하여 출력값 \( y = f(x) \)를 학습한다.
- 입력값 \(x\)의 정보는 완전히 변환되어 사라지고, 매번 새로운 정보를 학습해야 한다.
- 층이 깊어질수록 학습해야 할 매핑 \(f(x)\)이 복잡해져 최적화가 어려워진다.
Residual Block(ResNet 방식)
- 출력값 \(y\)는 \( y = f(x) + x \)로 표현된다.
- 입력값 \(x\)를 그대로 보존하면서 추가로 학습해야 할 정보량 \(f(x)\)만 학습한다.
- 기존 정보가 보존되기 때문에 최적화가 쉬워지고 학습의 안정성이 높아진다.
Residual Block을 이해하기 위해 학습 과정을 건축 작업에 비유해 보자.
- 모든 설계를 처음부터 완성해야 하는 건축 방식 (Plane Layer)
- 건축을 진행할 때, 모든 단계를 처음부터 완전히 새로 설계하고 건설해야 한다고 가정하자.
- 이전에 지어진 구조물을 참고하지 않고 새로운 설계도를 작성하고 모든 작업을 새롭게 시작해야 한다.
- 이 방식은 작업량이 많아지고, 단계가 많아질수록 실수와 수정의 여지가 커지며 효율성이 떨어진다.
- 기존 구조를 유지하며 추가적으로 설계하는 건축 방식 (Residual Block)
- 이미 지어진 구조물을 그대로 유지하며, 필요한 부분에 새로운 층이나 장치를 추가한다고 가정하자.
- 기존에 지어진 구조물을 활용하기 때문에, 새로운 작업은 추가적인 설계나 보완 작업에만 집중할 수 있다.
- 이 방식은 이전 작업물을 활용하므로 작업량이 줄어들고, 수정도 쉽다.
Residual Block의 출력값은 \(H(x)\) = \(F(x) + x\)로 정의되며, 이 과정에서 입력값 \(x\)와 출력값 사이의 차이를 잔차(residual)로 간주한다. 학습이 진행되면서 \(F(x)\)는 \(H(x) - x\)(잔차, residual)는 점차 0에 가까워지며, 이는 네트워크가 점점 안정화되고 최적화가 용이해짐을 의미한다. 이 특징 때문에 Residual Network(ResNet)라는 이름이 붙었다.
ResNet의 특징
- 구조의 간단함
- 기존 네트워크 구조를 크게 변경하지 않고도 입력과 출력 사이에 shortcut(Skip-Connection)을 추가하여 구현할 수 있다.
- 입력값 \(x\)가 그대로 출력에 연결되기 때문에 추가적인 파라미터가 필요하지 않다.
- 덧셈 연산만 추가되므로, 연산량 증가가 거의 없다.
- 효율적인 학습
- 네트워크는 \(F(x)\)라는 단순한 잔차만 학습하면 되므로, 깊은 네트워크에서도 기울기 소실 문제(vanishing gradient)가 완화된다.
- 학습이 진행되면서 잔차 \(F(x)\)가 작아지고, 시스템이 점차 안정화된다.
- 성능 향상
- 이러한 구조적 단순함과 효율성 덕분에 ResNet은 매우 깊은 네트워크에서도 안정적으로 학습할 수 있으며, 기존 모델에 비해 높은 성능을 달성할 수 있었다.
Skip-Connection(Shortcut-Connection), Identity mapping, Pre-Activation 등의 특징은 이어서 다루도록 하자.
3. ResNet의 구조
ResNet은 VGG-19의 구조를 기반으로 설계되었다. VGG-19처럼 연속적인 컨볼루션 층을 사용하는 구조를 따르면서도, 더 깊은 네트워크를 만들기 위해 컨볼루션 층을 추가했고, 최적화 문제를 해결하기 위해 shortcut 연결을 도입했다. ResNet의 34층 네트워크는 shortcut 연결을 포함한 구조이며, 아래 그림에서 shortcut 연결을 제거한 plain 네트워크외 비교할 수 있다.

34층 ResNet에서는 처음 레이어를 제외하고, 모든 컨볼루션 층에서 동일한 크기의 필터를 사용했다. 이러한 균일한 필터 크기는 모델의 설계를 단순화하면서도 효과적으로 특징을 학습할 수 있도록 한다.
또한, 네트워크의 깊이가 증가함에 따라 특성맵의 크기가 stride=2를 사용하는 풀링이나 컨볼루션 연산을 통해 절반으로 줄어드는 과정이 반복된다. 이때, 특성맵의 깊이(depth, 채널 수)는 이전 단계의 2배로 증가한다. 예를 들어, 특성맵의 크기가 56×56에서 28×28로 줄어들면, 특성맵의 깊이는 128에서 256으로 증가한다. 이는 네트워크가 더 많은 채널을 통해 더 풍부한 특징을 학습할 수 있도록 설계된 방식이다.
4. ResNet의 성능 비교

ResNet의 18-Layer 구조는 각 블록에서 사용된 Residual Block과 컨볼루션 계층의 수를 기반으로 계산된다. 위 표는 18층, 34층, 50층, 101층, 152층의 ResNet이 어떻게 구성되어 있는가를 나타낸다.
다음은 18-Layer 네트워크 구조를 계산하는 과정이다.
18-Layer 구조 세부 분석
- conv1 (입력 계층)
- 첫 번째 계층은 7×7 컨볼루션 필터(64 채널, stride 2)로 구성된다.
- 이 계층은 단일 계층으로 계산된다.
→ 1개
- conv2_x
- 이 블록에는 Residual Block 2개가 포함된다.
- 각 Residual Block은 2개의 3×3 컨볼루션 계층으로 구성된다.
- 따라서, 2×2=4개의 계층이 있다.
→ 4개
- conv3_x
- 이 블록도 Residual Block 2개로 구성된다.
- 각 Residual Block은 동일하게 2개의 3×3 컨볼루션 계층으로 구성된다.
- 따라서, 2×2=4개의 계층이 있다.
→ 4개
- conv4_x
- 이 블록 역시 Residual Block 2개로 구성된다.
- 각 Residual Block은 2개의 3×3 컨볼루션 계층으로 구성된다.
- 따라서, 2×2=4개의 계층이 있다.
→ 4개
- conv5_x
- 마지막 블록에는 Residual Block 2개가 포함된다.
- 각 Residual Block은 2개의 3×3 컨볼루션 계층으로 구성된다.
- 따라서, 2×2=4개의 계층이 있다.
→ 4개
- 출력 계층
- Global Average Pooling 및 Fully Connected Layer로 구성된다.
- 이 계층은 단일 계층으로 계산된다.
→ 1개
각 블록에서 계층의 수를 모두 합치면 다음과 같이 계산된다.
1(conv1)+4(conv2_x)+4(conv3_x)+4(conv4_x)+4(conv5_x)+1(출력 계층)=18계층

ResNet에서 Layer가 깊을수록 더 나은 성능을 보여준다는 것은 위 표를 참고하자. CIFAR-10과 CIFAR-100은 머신러닝 이미지 분류에 사용되는 데이터셋으로, 각각 10개와 100개의 클래스로 분류된다.
표에서 알 수 있듯이, CIFAR-10과 CIFAR-100 모두 ResNet의 레이어가 깊어질수록 에러율이 감소했다. 이는 Residual Block이 네트워크의 깊이가 증가해도 학습이 안정적으로 이루어지도록 돕는다는 것을 보여준다.
Baseline과 Pre-activation에 대한 내용은 이후에 다룰 예정이다.
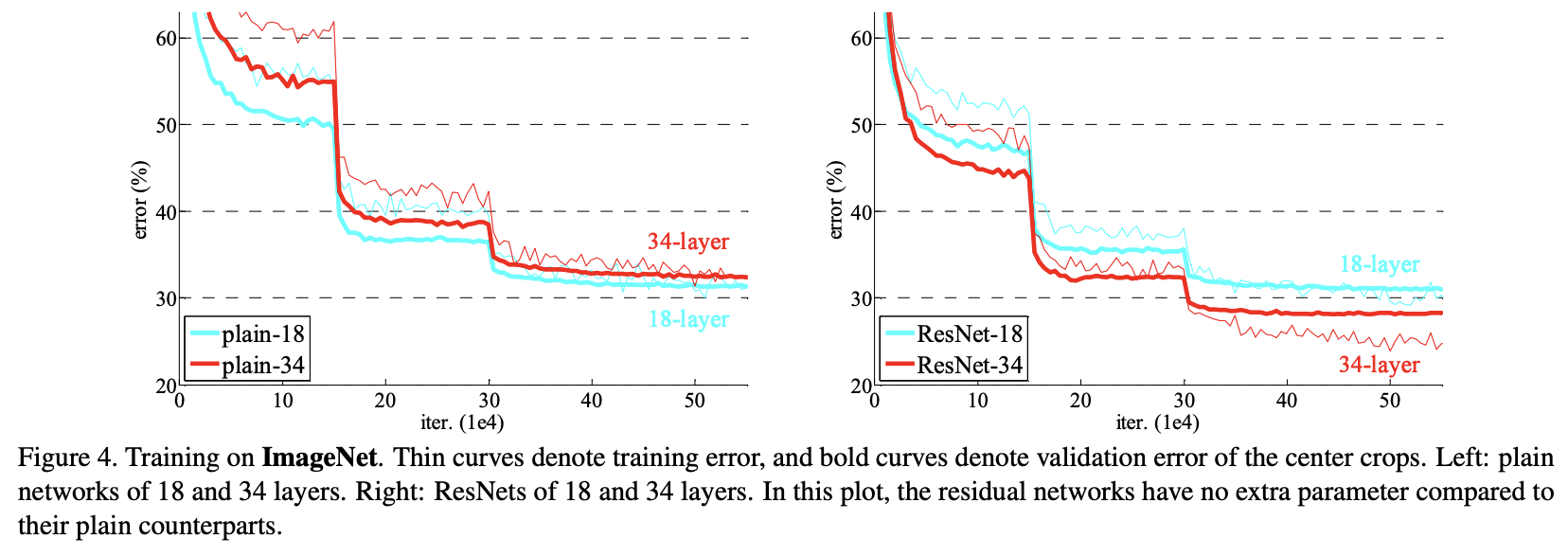
논문의 저자들은 Residual Block의 효과를 검증하기 위해 ImageNet 데이터셋에서 18층과 34층의 plain 네트워크와 ResNet의 성능을 비교했다.
- 왼쪽 그래프
- Plain 네트워크에서는 네트워크가 깊어질수록 에러가 오히려 증가했다.
- 특히, 34층의 plain 네트워크가 18층의 plain 네트워크보다 성능이 더 나빴다.
- 이는 깊은 네트워크에서 기울기 소실(vanishing gradient) 문제가 발생했기 때문으로 해석된다.
- 오른쪽 그래프
- ResNet에서는 네트워크가 깊어질수록 에러가 감소했다.
- 이는 shortcut 연결을 통해 입력 정보를 보존하고, 잔차(residual)를 최소화하며 학습한 효과 덕분이다.
5. ResNet 심화
5.1. Residual Block
ResNet의 핵심은 Residual Block으로, 이 블록은 2개 이상의 Convolutional Layer와 skip-connection을 활용하여 설계되었다. 블록을 쌓아 네트워크를 만들며, 하나의 블록의 구조와 수식은 아래 그림과 같다.


위 그림의 Residual Block은 \(l\)번 째 블록으로 \(x_l\)을 입력으로 받고, Skip-Connection인 \(h(x_l)\)과 Convolutional layer \(F(x_l, W_l)\)를 통과한 결과의 합으로 \(y_l\)을 출력한다. 마지막으로 출력 \(y_l\)을 활성 함수를 통과시키면 다음 블록의 입력인 \(x_{l+1}\)이 된다.
Vanishing Gradient 방지 원리
Residual Block의 설계는 Deep 네트워크에서도 기울기 소실(vanishing gradient) 문제를 방지한다. 이를 수식과 함께 설명한다.
Residual Block은 다음과 같은 수식으로 표현된다.
1. 일반화된 수식
여러 레이어로 구성된 Residual Block의 출력을 일반화하면 다음과 같이 표현할 수 있다.


Residual Block의 핵심은 Identity Mapping을 통해 입력 \(x_l\)를 그대로 다음 layer로 전달하는 경로를 제공한다는 점이다. 이로 인해 역전파 과정에서 기울기가 소실되는 문제를 효과적으로 완화할 수 있다.
2. Residual Block의 확장 표현
네트워크가 L개의 층으로 이루어져 있고, \(x_L\)가 \(l\)번째 층의 입력 \(x_l\)으로부터 만들어졌다고 가정하면, 다음과 같은 식을 유도할 수 있다.
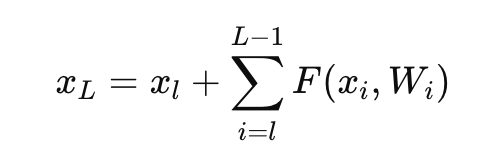

이 식은 Residual Block이 identify Mapping을 통해 입력 값을 그대로 유지하면서, 그 위에 Residual Function의 출력을 추가로 더하는 구조를 수학적으로 표현한 것이다.
3. 역전파에서 Gradient 계산 : Chain Rule 적용
Loss 함수 에 대해 역전파를 진행할 때, 입력 \(x_l\)에 대한 기울기 \( \frac{\partial \epsilon}{\partial x_l}\)를 계산한다. 체인 룰을 적용하면 다음과 같다.
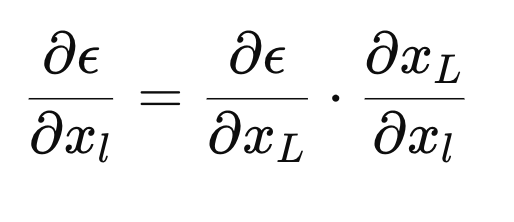
\( \frac{\partial x_L}{\partial x_l}\)를 구하는 과정이 중요하다.
4. \( \frac{\partial x_L}{\partial x_l}\)의 유도
위에서 \(x_L\)가 다음과 같이 정의된 것을 사용한다.

이를 \(x_l\)에 대해 미분하면

여기서 마지막 항은 Residual Function \(F(x+i, W_i)\)가 \(x_l\)에 미치는 영향을 나타낸다. Residual Function \(F(x+i, W_i)\)는 \(x_l\)과 \(W_i\)를 입력으로 받아 여러 층을 거치면서 계산되므로, 이 부분의 기울기는 가중치 \(W_i\)와 입력 \(x_l\) 모두에 의존한다.
5. 최종 Gradient 계산
Gradient를 구할 때 위 식을 다시 대입하면
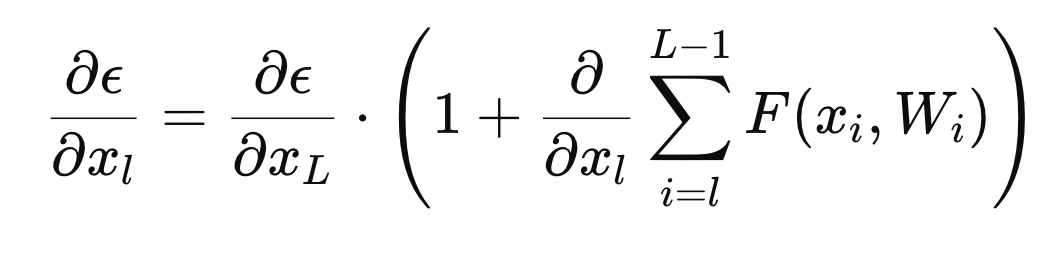
먼저 (1) 앞 부분의 식 \( \frac{\partial \epsilon}{\partial x_L}\)은 가중치 layer와는 무관하게 다이렉트로 전파되는 정보이다. 따라서 정보는 어떤 레이어든 같은 정보가 전파된다.
(2) 뒷 부분의 식 \(\frac{\partial \epsilon}{\partial x_L} \cdot \frac{\partial }{\partial x_l} \sum_{i=1}^{L-1} F(x_i, W_i)\)은 가중치 layer를 거쳐 전파되는 정보이다.
역전파(Backward Propagation) 과정에서 \( \frac{\partial \epsilon}{\partial x_l}\)이 0이 되려면, weight layer를 통해 전파된 값이 -1이 되어야 한다. Skip-Connection에서 전달된 값 1과 상쇄되기 때문이다.
하지만 실제 학습에서는 전체 데이터를 한 번에 학습하지 않고, 데이터의 일부를 나누어 사용하는 Mini-Batch 방식이 일반적으로 사용된다. 이 방식에서는 모든 Mini-Batch에서 역전파 값이 정확히 -1이 되는 경우는 거의 불가능하다. 따라서 \( \frac{\partial \epsilon}{\partial x_l}\)는 항상 0이 아닌 값을 가지게 된다.
결과적으로, 역전파 과정에서 기울기가 0에 가까워지지 않기 때문에 Residual Block에서는 Vanishing Gradient(기울기 소실) 문제가 발생하지 않는다.
5.2. Skip-Connection
Identity Mapping은 입력을 그대로 출력으로 전달하는 방식으로, 수학적으로는 다음과 같이 표현된다.

이는 입력 \(x\)가 아무런 변경 없이 다음 층으로 전달되는 것을 의미한다. Residual Block에서 Identity Mapping을 사용하면, 입력 신호가 손실 없이 다음 층으로 전달되어 Vanishing Gradient(기울기 소실) 문제를 방지하는데 매우 효과적이다.
그렇다면, 만약 Skip-Connection에서 Identity Mapping을 사용하지 않으면 어떻게 될까?
이미지에서 설명된 것처럼, Skip-Connection에서 Identity Mapping 대신 Modulating Scalar λ를 사용하여 다음과 같이 정의한다.
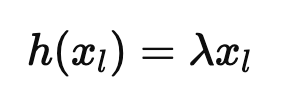
여기서 는 Modulating Scalar로, 입력에 일정한 스칼라 값을 곱한 값을 전달한다.
Residual Block의 출력 \(x_{l+1)\)은 다음과 같이 표현된다.

이를 L개의 층으로 확장하면 (한줄 한줄 써내려가면 식이 유도됨을 알 수 있을 것이다.)
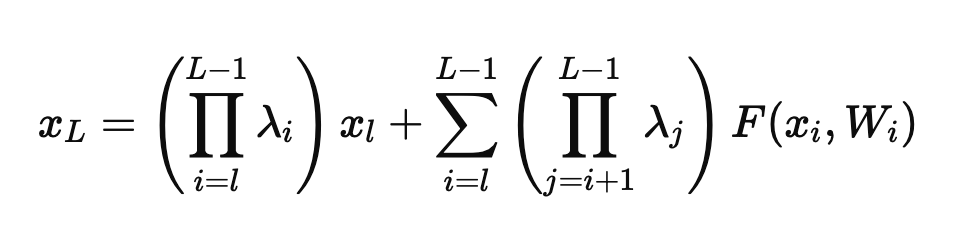
여기서 각 항목이 의미하는 바는 다음과 같다.
(1) 앞 항
- 이 여러 층을 거치면서 전달될 때, 각 층에서 곱해지는 스칼라 값 λ의 곱을 의미한다.
- 만약 이라면, 이 값은 지수적으로 감소하여 \(x_l\)이 거의 0에 가까워진다. 이로 인해 Vanishing Gradient 문제가 발생한다.
(2) 뒷 항
- Residual Function \(F(x_i, W_i)\)의 영향을 합산하는 항목이다.
- 여기서도 λ의 값이 작을 경우, Residual Function의 기여도 또한 감소하게 된다.
λ 값을 설정할 때,
- λ<1
- 층이 깊어질수록 \( \prod \lambda_i \)가 0에 가까워지고, 입력 정보가 소실됩니다. 결과적으로 Vanishing Gradient가 발생한다.
- λ>1
- 층이 깊어질수록 \( \prod \lambda_i \)가 기하급수적으로 증가하여 Gradient Explosion(기울기 폭발)이 발생한다.
결론적으로 Identity Mapping을 사용하면 λ=1이 되어, 입력 \(x_l\)이 그대로 다음 층에 전달된다. 이를 통해 Skip-Connection이 안정적으로 작동하며, Gradient 소실이나 폭발 문제가 발생하지 않는다.

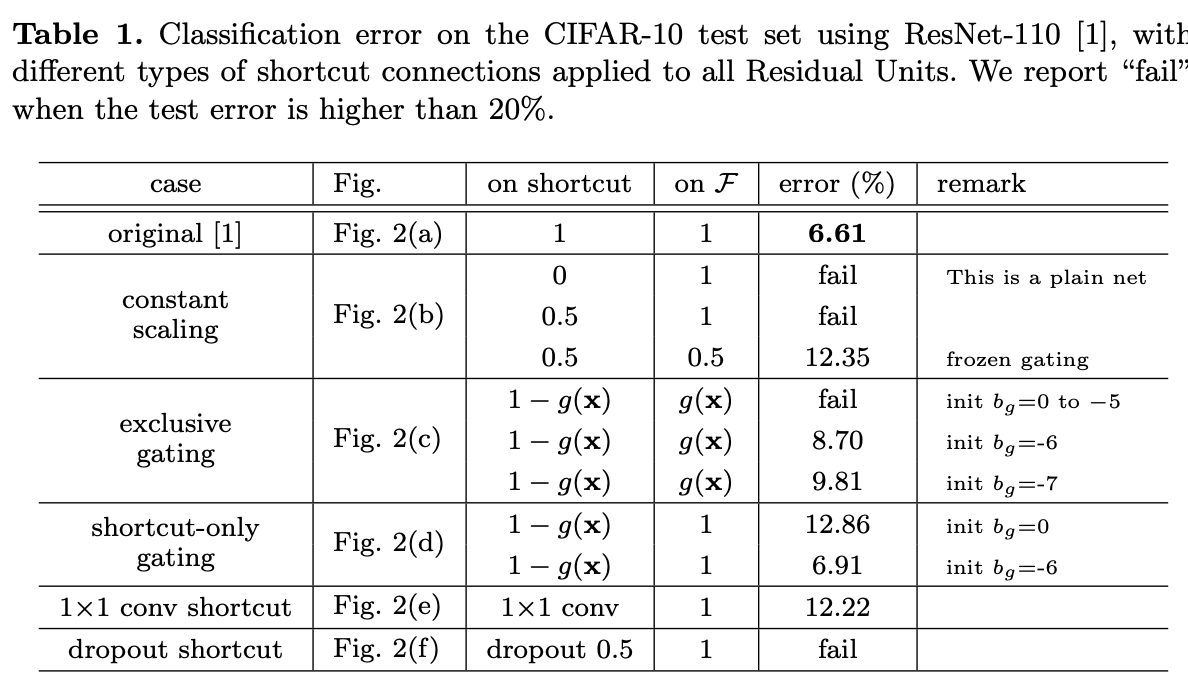
참고로, 논문에서는 Skip-Connection의 형태를 6가지로 설정하고(Identity Mapping이 아닌 경우도 있음) 학습하여 성능을 평가한 결과, 입력을 그대로 전달하는 기존 구조가 가장 성능이 좋음을 확인하였다.
이는 Skip-Connection에 추가적인 변환이나 조작(예 : 활성화 함수, 스케일링 등)을 적용하면 정보 전달 과정에 손실이 발생할 수 있고, 최적화 과정이 복잡해지는 결과를 초래한다는 것을 알 수 있다.
5.3. Pre-Activation
앞 장의 실험에서는 활성함수 \(f\)가 Identity-Mapping이라고 가정하였다. 즉, shortcut 연결이 입력 데이터를 변형 없이 그대로 전달해야 성능이 좋다고 결론 내렸다. (여기서 말하는 Identity Mapping은 Skip-Connection이 데이터를 변형하지 않는 것을 의미한다.)
하지만 ResNet에서 사용하는 Residual Block에서는 활성함수 \(f\)가 ReLU 함수로 설정되어 있으며, 이는 shortcut 신호와 잔차 \(F(x_l, W_l)\)가 합쳐진 뒤에 적용된다. 쉽게 말해, 쉽게 말해, Skip-Connection을 통해 전달된 입력과 Residual Function의 출력이 합쳐진 결과에 ReLU가 적용된다는 뜻이다. 이는 합쳐진 신호가 ReLU를 통과하면서 변형될 가능성이 있음을 의미한다.
논문의 저자들은 이를 해결하기 위해, 활성 함수 \(f\)도 Identity Mapping처럼 동작하도록 새로운 Residual Block 구조를 제안하였다. 아래 그림은 저자들이 제안한 다양한 구조를 보여주며, 이 구조들을 사용해 CIFAR-10 데이터셋에서 학습을 진행한 후 테스트 데이터에서의 에러율을 나타낸다. 이 실험에서는 Weight Layer로 2개의 Convolutional Layer 대신 Bottleneck 구조를 사용하였다.


- (a): ResNet 논문에서 제안된 가장 기본적인 구조이다. 이 구조에서는 shortcut 신호와 Residual Function \(F(x_l, W_l)\)의 결과를 합치는 addition 연산 뒤에 ReLU 활성 함수가 적용된다.
- (b) : 마지막 Batch Normalization을 addition 연산 뒤로 옮긴 구조이다. 하지만 학습 결과, 원래 형태(post-activation)보다 성능이 나빠졌으며, 테스트 데이터에서 에러율이 8.17%로 나타났다.
- (c): 활성 함수 ReLU를 weight layer 안으로 옮긴 구조이다. 이 방식은 ReLU를 통과한 신호를 shortcut 신호와 합치는 구조를 만든다. 그러나 ReLU의 특성상, 신호 값의 범위가 양수가 되며, forward propagation 시 신호가 양수로 편향된다. 이는 네트워크의 표현력을 낮추어 성능 저하로 이어진다.
여기서 저자들은 ResNet의 신호 범위가 양수가 아닌 전체 실수 영역(-∞ ~ ∞)을 가져야 한다고 주장하였다. 따라서 뒤에서 제안되는 새로운 구조들은 신호 범위를 전체 실수 영역으로 확장하도록 설계되었다.
- (d): ReLU만 weight 앞에 위치시킨 구조이다. 이는 기본 구조(a)보다 약간 낮은 성능을 보인다. 그러나 신호 범위가 양수로 제한되지 않기 때문에 (c)보다는 나은 성능을 보여준다.
- (e): Batch Normalization과 ReLU를 모두 weight 앞에 위치시킨 full pre-activation 구조이다. 이 구조는 기본 구조보다 좋은 성능을 보여주며, 현재까지 제안된 구조 중 가장 우수한 성능을 기록하였다.
(d)와 (e) 구조는 비대칭적(asymmetric) 구조로, 신호가 weight layer를 통과하기 전에 활성화 함수(ReLU와 Batch Normalization)를 먼저 통과하도록 설계되었다. 기본 구조(a)에서 활성화 함수가 weight layer의 출력에만 영향을 주도록 한 것과 달리, (d)와 (e)는 weight layer의 입력 신호를 조정하여 성능을 향상시킨다.
새로운 pre-activation 구조(활성함수와 BN의 위치를 weight layer 앞쪽으로 이동시키는 설계 방식)는 residual unit의 활성화 함수와 Batch Normalization의 위치를 변경함으로써 네트워크가 더 나은 학습 및 일반화 성능을 가지도록 설계되었다.
좀 더 쉬운 이해를 위해서 기본 구조(a)와 Pre-Activation 구조(e)의 활성화 방식을 비교하여 설명하겠다.
1. 기본 구조(a)의 활성화 방식
- 입력 \(x_l\)이 Residual Block의 weight layer(Convolutional Layer 등)를 통과한다.
- weight layer의 출력이 Batch Normalization과 ReLU 활성화를 통과한다.
- 마지막으로 shortcut 신호와 잔차(Residual Function) \(F(x_l, W_l)\)의 결과를 addition 연산으로 합친다.
- shortcut 신호 \(x_l\)는 weight layer와 상관없이 그대로 addition 연산으로 전달된다.
- ReLU는 잔차 계산 과정에만 영향을 주며, shortcut 신호에는 영향을 미치지 않는다.
이 구조에서는 활성화 함수(ReLU)가 shortcut 신호와 weight layer의 출력 신호를 합친 후 적용되므로, weight layer에 들어가는 입력 신호는 그대로 전달된다.
2. Pre-Activation 구조(e)의 활성화 방식
- Pre-Activation 구조는 다음과 같이 변경된다.
- 입력 \(x_l\)이 weight layer를 통과하기 전에 Batch Normalization과 ReLU 활성화 함수를 먼저 적용받는다.
- Batch Normalization과 ReLU를 통과한 정제된 신호가 weight layer로 전달된다.
- weight layer의 출력은 추가적으로 Batch Normalization을 거친다.
- 이후, 이 출력 \(F(x_l, W_l)\)과 shortcut 신호 \(x_l\)가 addition 연산으로 합쳐진다.
- 활성화 함수(ReLU)와 Batch Normalization이 weight layer 입력 신호에 직접 작동한다.
- 이로 인해 weight layer가 더 정제된 신호를 입력받아 학습이 안정적으로 이루어진다.
- 또한, 합쳐진 신호에 ReLU를 적용하는 대신 weight layer 입력에 ReLU를 적용하여 네트워크의 표현력과 성능이 향상된다.
이 방식에서는 활성화 함수(ReLU)가 weight layer에 입력되기 전에 적용되므로, weight layer가 더 정제된 신호를 입력받게 된다.


Table 3에서 Depth를 110부터 1001까지 바꿔가며 CIFAR-10/100 데이터셋에서 테스트해본 결과 모든 경우에 pre-activation 구조가 성능이 좋은 것을 볼 수 있다. 따라서 pre-activation 이 post-activation보다 더 성능이 뛰어나다고 볼 수 있다.
5.4. Bottleneck
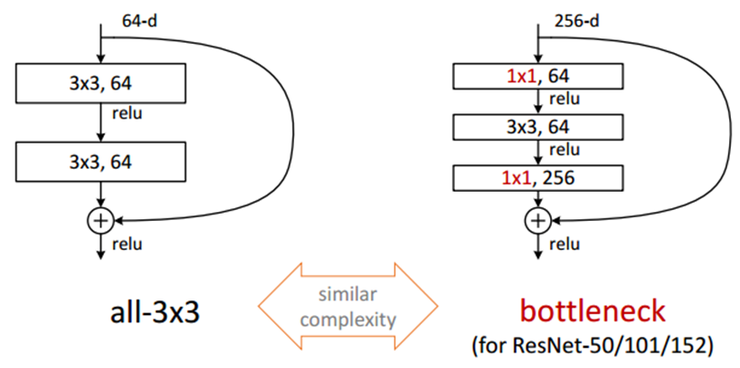
Residual Block은 1, 3x3, 의 Conv 연산으로 구성된다. 이를 Bottleneck 구조라고 부르는 이유는, 중간에 차원을 줄였다가 다시 늘리는 과정이 병목처럼 보이기 때문이다.
Bottleneck 구조의 목적 -> 연산 시간을 줄이기 위해 설계되었다.
- 첫 번째 1×1 Convolution: 입력 데이터의 채널 수(차원)를 줄인다. 이는 GoogLeNet의 Inception 구조나 NIN(Network-in-Network)에서 사용된 방식과 유사하다.
- 두 번째 3×3 Convolution: 차원을 줄인 상태에서 핵심 연산을 수행한다.
- 마지막 1×1Convolution: 줄였던 채널 수를 다시 원래대로 확장한다.
결과적으로, 3×3 Convolution두 개를 직접 연결한 구조에 비해 연산량을 크게 절감할 수 있다.
연산량을 직접 비교해보자.
- Bottleneck 미사용 구조
- 두 개의 3×3 Convolution을 사용하는 경우
- 3×3×64×2=1152 -> 총 1152개의 파라미터가 필요하다.
- Bottleneck 구조:
- 1×1, 3×3, 1×1 Convolution을 사용하는 경우
- (1×1×64)+(3×3×64)+(1×1×256)=896 -> 총 896개의 파라미터가 필요하며, 이는 Bottleneck 미사용 구조 대비 약 22% 감소한 수치이다.
Bottleneck 구조는 Residual Block에서 차원을 효율적으로 조정하여 연산량을 줄이고, 학습 속도를 개선하는 중요한 설계 방식이다. 차원을 줄이면서도 핵심 정보를 보존할 수 있어 모델의 효율성과 성능을 동시에 높일 수 있다.
6. 성능 분석
6.1. post-activation VS pre-activation
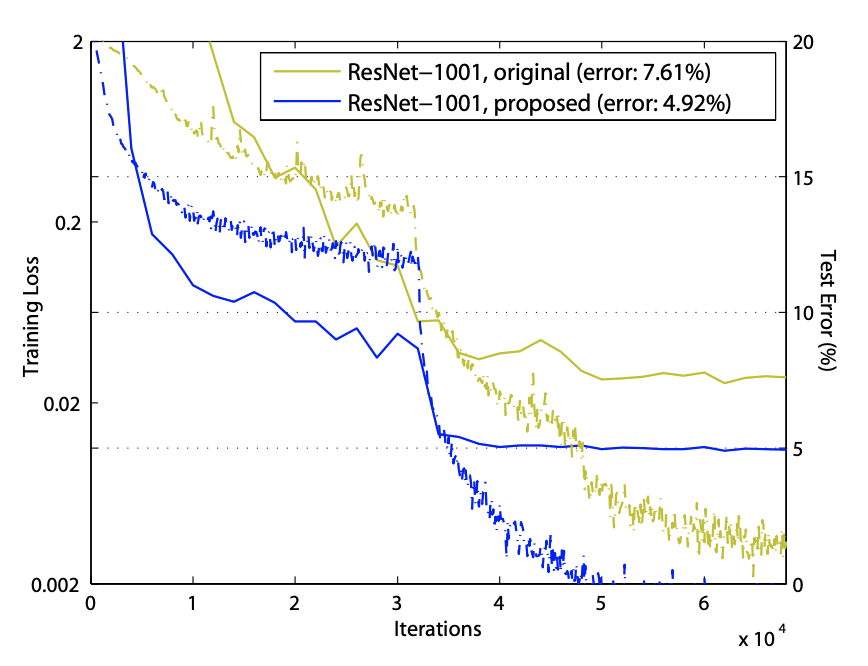
Pre-Activation 구조는 활성 함수 \(f\)가 identity mapping처럼 작동할 수 있도록 설계되어 신호 손실을 최소화하고 네트워크 최적화가 더 용이해진다. 반면, Post-Activation 구조에서는 Residual Block 내부의 ReLU 활성 함수가 음수 신호를 모두 제거하며, 이러한 신호 손실로 인해 네트워크가 깊어질수록 학습 성능이 저하되는 문제가 발생한다.
Post-Activation 구조에서는 아래의 가정이 만족되지 않는다.
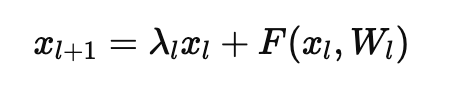
ReLU로 인해 음수 값이 제거되며 신호 손실이 누적되어 초기 학습 단계에서 학습이 더디게 진행된다. ResNet-1001 실험 결과, Post-Activation 구조를 사용한 모델은 초반 학습 속도가 느리며 최종적으로 에러율이 7.61%에 달한다. 반면, Pre-Activation 구조에서는 초반 학습부터 안정적이고 빠르게 진행되며, 최종적으로 에러율이 4.92%로 더 나은 성능을 보여준다.
Pre-Activation 구조는 ReLU로 인한 신호 손실을 줄이고 Residual Block의 신호 전달 효율성을 높여, 깊은 네트워크에서 더 안정적인 학습과 성능 향상을 보장한다.
6.2. Batch-Normalization 적용 여부에 따른 비교
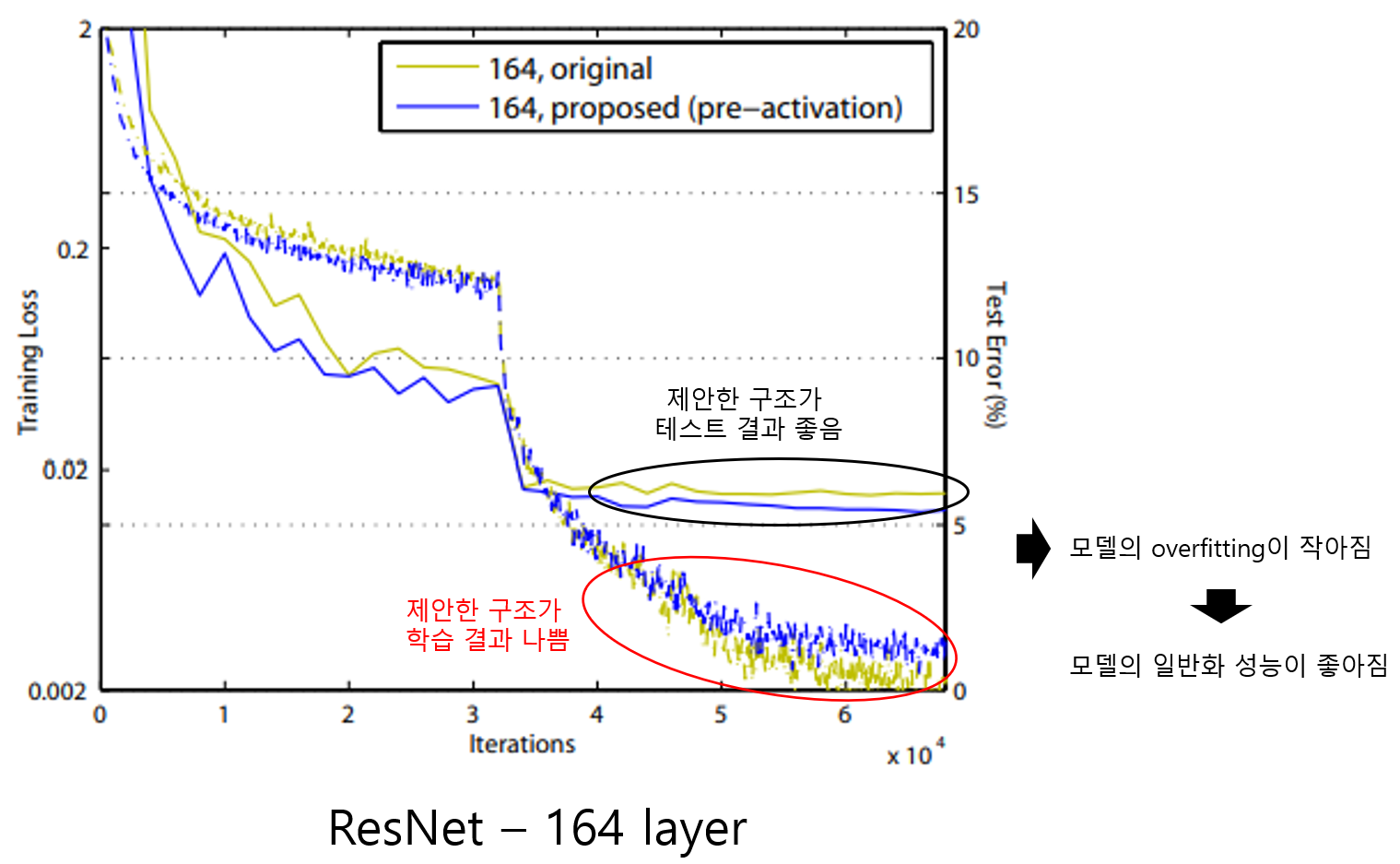
Pre-Activation 구조는 Batch Normalization을 통해 신호가 정규화되며, 이로 인해 네트워크의 일반화 성능이 향상된다. 이는 과적합을 줄이고 테스트 데이터에서 더 좋은 성능을 발휘하도록 돕는다.
위 그림은 CIFAR-10 데이터셋에서 ResNet-164를 학습한 결과를 보여준다. 테스트 성능은 Pre-Activation 구조가 기존 Post-Activation 구조보다 우수하지만, 학습 성능은 기존 구조가 더 높게 나타난다.
이러한 차이가 발생하는 이유는 Pre-Activation 구조에서 신호가 Batch Normalization을 먼저 통과하여 정규화된 후 weight layer로 전달되기 때문이다. 신호가 정규화되면서 학습 단계에서 과적합이 줄어들고 네트워크가 더 일반화된 특성을 학습하게 된다.
학습 단계에서는 Pre-Activation 구조가 기존 구조에 비해 성능이 낮을 수 있다. 기존 구조는 과적합이 쉽게 이루어져 학습 데이터에 맞는 성능은 더 높게 나올 가능성이 있다. 그러나 테스트 단계에서는 Pre-Activation 구조가 일반화가 잘 이루어진 결과로 인해 기존 구조보다 더 나은 성능을 보인다.
일반화 성능은 학습 데이터뿐만 아니라 테스트 데이터에서도 높은 성능을 발휘하는 능력을 의미한다. Pre-Activation 구조는 Batch Normalization을 통해 학습 데이터에 과적합되지 않으면서 테스트 데이터에서도 좋은 결과를 얻을 수 있도록 한다.
6.3. 다른 네트워크와의 성능 비교


Table 5에서는 ImageNet 실험에서 ResNet-152, ResNet-200, Inception-v3를 비교한 결과가 제시된다. 실험 결과, 기본 구조의 Residual Block을 사용한 ResNet-152와 ResNet-200을 비교했을 때, ResNet-152가 더 나은 성능을 보인다. 학습 과정에서는 ResNet-200의 training error가 더 낮았지만, 이는 overfitting이 발생한 것으로 해석되었다.
반면, 일반화 성능이 더 좋은 pre-activation 구조를 사용한 ResNet에서는 ResNet-200이 ResNet-152보다 성능이 더 우수한 것으로 나타났다. 이는 post-activation 구조에서 ReLU에 의해 신호 손실이 발생하지만, pre-activation 구조에서는 이러한 신호 손실이 없기 때문이다. 네트워크가 깊어질수록 더 많은 활성 함수를 통과하기 때문에 post-activation 구조에서 신호 손실은 점점 커지지만, pre-activation 구조에서는 이러한 문제가 발생하지 않는다.
실험 결과, pre-activation 구조를 사용한 경우 ResNet-152와 ResNet-200 모두 성능이 개선되었다. ResNet-152에서는 0.2% 정도의 성능 향상이 있었지만, ResNet-200에서는 1.1%의 성능 향상이 나타났다. 이는 네트워크의 층이 깊어질수록 pre-activation 구조가 더 큰 효과를 발휘한다는 것을 보여준다.
결론적으로, pre-activation 구조를 적용하고 single crop과 같은 augmentation 기법을 사용한 ResNet-200이 가장 높은 성능을 기록하였다.




