논문 링크: 2112.10752
Abstract

- Diffusion Model은 고품질 이미지 생성에 탁월하지만, pixel space에서 직접 학습할 때 막대한 계산량과 시간이 소요된다
- 본 논문에서는 먼저 사전 학습된 강력한 Autoencoder를 사용해 이미지를 latent space로 압축한 뒤, 해당 공간에서 Diffusion Model을 학습하는 방안(Latent Diffusion Model, LDM)을 제안한다.
- 이 방식은 기존 pixel space 기반 Diffusion 대비 학습 비용과 inference(sampling) 비용을 크게 절감함과 동시에, 다양한 조건(예: 텍스트, 세그멘테이션 맵 등)을 유연하게 적용할 수 있다.
- 또한 cross-attention layers를 모델 구조에 통합함으로써, DMs를 텍스트나 bounding boxes 같은 conditioning input을 다룰 수 있는 강력하고 유연한 Generator로 확장하였다.
- 이 구조 덕분에 convolutional 방식으로 고해상도 이미지 합성이 가능하게 되었으며, 다양한 task에서 활용될 수 있다.
- Inpainting, Super-Resolution, Text-to-Image Synthesis 등 여러 이미지 생성·복원 과업에서 경쟁력 있는 성능을 달성하며, 고해상도(1024×1024)까지 효율적으로 확장 가능함
1. Introduction
High-Resolution Image Synthesis의 한계와 문제점

- DMs는 likelihood-based 모델로서 mode-covering 특성을 갖고 있어, 데이터의 인지할 수 없는 details까지 모델링하려는 경향이 있다. 이로 인해 불필요하게 많은 계산 자원이 소모된다.
- 학습 및 추론 과정에서 고차원 RGB 이미지 공간에서 반복적인 함수 평가와 gradient 계산이 필요
- 이미 학습된 모델이라 하더라도, inference 비용이 크기 때문에 실제 활용에도 제한이 존재한다. 예: 25~1000 step의 sequential한 연산이 필요하다.
Latent Space로의 전환

- 이러한 문제를 해결하고 연산 비용은 줄이면서 모델의 성능과 유연성을 유지하기 위해, 본 연구는 pixel space에서 학습된 diffusion model을 분석하는 데서 출발한다.
- Rate-distortion trade-off 분석에 따르면, likelihood 기반 모델의 학습은 다음의 두 단계로 구분할 수 있다:
- Perceptual compression 단계: 고주파 세부정보를 제거하되, semantic variation은 거의 학습하지 않음.
- Semantic compression 단계: 실제로 의미론적 구성요소를 학습하는 단계.
- 따라서, 본 논문에서는:
- Perceptual 관점에서 동등하지만 계산적으로 더 효율적인 공간(latent space)을 찾고,
- 그 공간에서 고해상도 이미지 합성을 위한 diffusion model을 학습하고자 한다.
- 이 latent space는 다음과 같은 점에서 pixel space보다 likelihood-based generative model에 더 적합하다:
- 의미 있는 정보(semantic bits)에 집중할 수 있으며, 계산 효율이 훨씬 높은 공간에서 학습이 가능하다.
- 이 latent space는 다음과 같은 점에서 pixel space보다 likelihood-based generative model에 더 적합하다:
- 학습을 두 단계로 분리:
- Autoencoder 학습: perceptually equivalent하면서도 효율적인 저차원 표현 공간을 학습
- Diffusion model 학습: 학습된 latent space에서 수행되므로, pixel space보다 훨씬 효율적
- 특히, 본 연구에서는 기존 연구들처럼 과도한 spatial compression을 필요로 하지 않는다.
- Latent space 자체가 이미 효율적이며, spatial dimensionality에 대해 더 나은 scaling 특성을 가지기 때문이다.
- 이 방식을 통해, single network pass만으로도 효율적인 이미지 생성이 가능하다.
2. Related Work
Generative Models for Image Synthesis
- GANs는 고해상도 이미지를 빠르게 생성할 수 있으나, 최적화가 어렵고 전체 데이터 분포를 잘 포착하지 못함.
- VAE 및 flow-based models는 학습이 안정적이고 고해상도 생성이 가능하지만, 이미지 품질은 낮음.
- Autoregressive models (ARM)는 정확하지만, 계산 비용이 높고 샘플링이 느려 고해상도에 부적합.
- pixel 기반 maximum-likelihood 학습은 고주파 세부 정보를 과도하게 학습하여 비효율적임.
- 해결책으로, latent space에서 ARM을 학습하는 two-stage 방법이 제안됨.
Diffusion Probabilistic Models (DMs)
- DMs는 density estimation과 이미지 품질 모두에서 SOTA 수준의 성능을 보임.
- 특히 UNet 기반 구조와 reweighted objective가 성능에 크게 기여.
- 그러나 pixel space에서 학습하고 추론하면 계산 비용이 매우 높고 느림.
- 본 논문의 LDMs는 latent space에서 diffusion을 수행하여, 효율성과 품질을 모두 확보함.
Two-Stage Image Synthesis
- 다양한 방법들이 two-stage 접근을 통해 성능과 효율성을 함께 추구함.
- VQ-VAE: discrete latent space + autoregressive prior.
- VQGAN: adversarial loss + perceptual loss를 활용하여 고해상도 이미지 생성에 유리.
- 하지만 이러한 접근은:
- 고압축률 → 정보 손실 및 성능 저하,
- 저압축률 → 계산 비용 증가라는 trade-off가 존재.
- LDMs는 convolutional backbone 덕분에 고차원 latent space에서도 효율적이며, 압축 수준을 유연하게 조절 가능하다.
Joint vs. Separate Training
- Joint 학습 방식은 encoding/decoding과 prior 학습을 동시에 수행하지만, 재구성과 생성 성능 간 균형 조절이 어렵다.
- Separate 방식은 보다 단순하며, 본 논문에서는 이 방식을 통해 성능과 효율성 모두 우수하게 달성함.
- 특히 본 논문의 접근은 일반 이미지보다 구조화된 이미지에 국한되지 않는다.
3. Method
Compressed Learning vs. Generative Learning의 분리
- compressive learning과 generative learning를 명시적으로 분리한다.
→ 이를 위해 autoencoding model을 사용하여, image space와 perceptually equivalant하지만 계산적으로 훨씬 간단한 latent space를 학습한다.
Pros
- 저차원 공간에서 sampling이 이루어지므로, diffusion model은 훨씬 계산 효율적이다.
- UNet 기반 DMs의 inductive bias를 그대로 활용할 수 있으며, 이미지처럼 spatial 구조를 가진 데이터에 특히 잘 작동하므로, 기존 연구들이 필요로 했던 과도한 압축률을 사용하지 않아도 된다.
- 범용적인 compression model을 하나 학습해두면, 같은 latent space를 활용하여 여러 generative model을 학습할 수 있으며, downstream task에도 활용 가능하다.
3.1 Perceptual Image Compression

- Autoencoder 구조
- Encoder $E$: 원본 이미지 $\mathbf{x}$를 downsampling factor $f$만큼 축소하여 latent vector $\mathbf{z} = E(\mathbf{x})$로 변환
- Decoder $D$: $\mathbf{z}$를 다시 upsampling하여 복원 이미지 $\hat{x} = D(z) = D(E(x))$ 생성
- downsampling factor는 f = H/h = W/w, $f = 2^m$로 로 다양한 실험 진행
- Latent Space Regularization 방식
- KL-regularization: VAE 유사 방식으로, 학습된 latent가 $\mathcal{N}(0,1)$과 가깝도록 가벼운 KL penalty을 준 방식 → 재구성 성능이 크게 손상되지 않도록 조절
- VQ-regularization: Decoder 내부에 Vector Quantization 레이어를 추가해, discrete codebook을 사용 → 표현력을 높이면서도 잡음 없는 공간을 확보
- VQGAN과 유사하나, quantization layer가 Decoder에 흡수된 형태
- Loss 구성
- Perceptual Loss(예: VGG 기반) + Patch-based Adversarial Loss(이미지 로컬 영역의 사실감을 위한 GAN Loss)
- 단순 L1·L2 Loss보다 시각적·구적 품질이 향상된 재구성을 달성
- Patch-based Adversarial: 이미지를 여러 patch로 나눠서 진짜/가짜를 판별 → local realism 확보, blurriness 완화
- 이 과정을 통해, 재구성($\hat{\mathbf{x}}$)이 원본( $\mathbf{x}$ )과 최대한 유사해지도록 학습
3.2 Latent Diffusion Models
- 기본 아이디어
- Diffusion Model은 데이터(이미지)에 점차 Gaussian Noise를 추가 한 뒤, 이를 역으로 제거(denoising)하는 과정을 학습
- pixel space에서 직접 노이즈를 주고받으면 연산량이 매우 커짐 → 이를 latent space로 옮겨 계산량을 줄임
- 식 (1): 기존 Diffusion Model의 손실$$\mathcal{L}_{\mathrm{DM}} = \mathbb{E}_{x,\; \epsilon \sim \mathcal{N}(0,1),\; t} \Bigl[ \|\epsilon - \epsilon_{\theta}( \mathbf{x}_t,\; t)\|_2^2 \Bigr].$$
- $\mathbf{x}_t$: 입력 $\mathbf{x}$에 $t$-step만큼 노이즈가 추가된 상태
- $\epsilon$: $\mathcal{N}(0,1)$에서 샘플링된 원본 노이즈
- $\epsilon_{\theta}(\mathbf{x}_t,t)$: 모델이 예측한 노이즈
- 이 기대값( $\mathbb{E}$)을 최소화함으로써, 노이즈를 성공적으로 제거하도록 학습
- Autoencoder 활용
- $\mathbf{z} = E(\mathbf{x})$: Autoencoder의 Encoder $E$를 통해 얻은 latent representation
- pixel space 대신 latent space에서 forward process(점진적 노이즈 추가)를 정의
- Loss Function (Reweighted Objective)
- Latent Space에서 노이즈화된 $\mathbf{z}_t$를 역으로 복원, reweighted objective를 이용해 perceptually 중요한 정보에 집중하는 것 핵심
- $\mathbf{z}_t$는 $\mathbf{z}$에 $t$-step 노이즈가 추가된 상태
- 식 (2): LDM 학습 목적$$L_{\mathrm{LDM}} := \mathbb{E}_{\mathcal{E}(x),\; \epsilon \sim \mathcal{N}(0,1),\; t} \Bigl[ \|\epsilon \;-\; \epsilon_{\theta}(\mathbf{z}_t,\; t) \|_{2}^{2} \Bigr].$$
- $\epsilon_{\theta}$: 네트워크(2D convolutional layer로 구성된 UNet)가 예측하는 노이즈
- $\mathbf{z}_t$: $\mathbf{z}$에 $t$-step 노이즈가 더해진 상태
- 이 식을 최소화하면, 모델이 $\mathbf{z}_t$에서 원본 $\mathbf{z}$를 복원(또는 $\epsilon$을 정확히 예측)하도록 학습
- 학습 시에는 $z_t$를 encoder $E$로부터 효율적으로 얻을 수 있고, 추론 시에는 latent space에서 생성한 $z$를 decoder $D$에 한 번(latent 공간 pure noise $z_T$에서 noise 단계적으로 제거하여 최종 $z_0$만 복원)통과시켜 이미지로 복원할 수 있다.
3.3 Conditioning Mechanisms
- 조건부 분포 $p(\mathbf{z} \mid y)$ 학습
- $y$: text, semantic maps, 또는 image-to-image 변환 입력 등 다양한 입력
- DM은 원리적으로 이런 conditional distribution을 모델링 가능하다.
- Cross-Attention
- UNet의 특정 중간 레이어에 Cross-Attention을 삽입
- Query: UNet 피처맵 (노이즈화된 $\mathbf{z}_t$에서 추출된 중간 표현)
- Key/Value: 별도 인코더(예: 텍스트 인코더)에서 추출된 임베딩
- $\text{Attention}(Q, K, V) = \text{softmax}\Bigl(\frac{QK^T}{\sqrt{d}}\Bigr)V$ 구조로,
- $Q = W_Q^{(i)} \cdot f_i(\mathbf{z}_t)$,
- $K = W_K^{(i)} \cdot \phi(y)$,
- $V = W_V^{(i)} \cdot \phi(y)$
- $f_i(\mathbf{z}_t)$는 UNet 내부의 (flattened) 중간 표현, $\phi(y)$는 도메인 특화 인코더의 출력한다.
- 조건부 학습: 식 (3)$$L_{\mathrm{LDM}} := \mathbb{E}_{\mathcal{E}(x),\; y,\; \epsilon \sim \mathcal{N}(0,1),\; t} \Bigl[ \|\epsilon - \epsilon_{\theta}(\mathbf{z}_t,\; t,\; \tau_{\theta}(y)) \|^2 \Bigr].$$
- $\tau_{\theta}(y)$: 조건 $y$를 임베딩한 결과(예: 텍스트 인코더 출력)
- $\epsilon_{\theta}(\mathbf{z}_t,\; t,\; \tau_{\theta}(y))$: 노이즈화된 latent $\mathbf{z}_t$와 조건을 동시에 입력받아 예측된 노이즈
- 이 손실을 최소화함으로써, 모델은 조건$y$에 맞춰 이미지를 생성(노이즈 제거)하는 방식을 학습한다.
즉,
- 조건부 입력 $(\mathbf{x}, y)$ 쌍에 대해,
- $\mathbf{x}$ → $\mathbf{z}$ (Autoencoder)
- $\mathbf{z}_t$ (노이즈 추가) + $\tau_{\theta}(y)$ (조건 임베딩) → UNet → 예측 노이즈 $\epsilon_{\theta}$
- Loss $\|\epsilon - \epsilon_{\theta}\|^2$을 최소화
- 이렇게 학습된 모델은 텍스트, 세그멘테이션 등 다양한 조건에 대응하는 이미지를 생성할 수 있다.

4. Experiments
4.1 Perceptual Compression Tradeoffs



- 다양한 downsampling factor $f$로 LDM을 학습한 결과, $f$가 너무 작으면(픽셀에 가깝게) 학습 속도가 느리고, 너무 크면 정보 손실이 커져 품질이 제한된다.
- 중간값(LDM-4, LDM-8)에서 학습 효율과 생성 품질의 균형점을 찾았다.
4.2 Image Generation with Latent Diffusion


- CelebA-HQ, FFHQ, LSUN 등 여러 데이터셋에 대해 unconditional LDM을 학습
- FID 및 Precision-Recall 평가에서 기존 모델(LSGM, GAN류)보다 우수하거나 유사한 성능을 달성하였다.
- 고해상도(256×256) 이미지 생성에서 mode coverage와 시각적 품질이 모두 향상되었다.
4.3 Conditional Latent Diffusion



- 텍스트, 세그멘테이션 등 다양한 조건을 Cross-Attention으로 처리
- 텍스트-이미지 모델: LAION 데이터로 학습 시, 사용자 정의 문장을 잘 반영하는 결과 확인
- MS-COCO 등 벤치마크 테스트에서 강력한 AR 모델이나 GAN류와 경쟁력 있는 FID 달성하였다.
- 256×256 해상도로 학습된 LDM은 512×1024 해상도와 같은 더 큰 해상도로 일반화할 수 있으며, 이는 풍경 이미지의 의미적 합성과 같은 공간적 조건이 있는 작업에 적용 가능하다.
4.4 Super-Resolution with Latent Diffusion


- Low-resolution 이미지를 입력으로 concat하여 super-resolution 모델 학습
- 단순(픽셀 기반) SR보다 FID 개선 및 사용자 선호도(테스트 설문) 높게 나타난다.
- SR3 등 기존 확산 기반 방법과 비교 시, FID는 개선·IS는 근소 열세 등 장단점 존재한다.
4.5 Inpainting with Latent Diffusion



- 이미지 일부를 마스킹한 뒤, 해당 영역을 새로운 컨텍스트로 채움
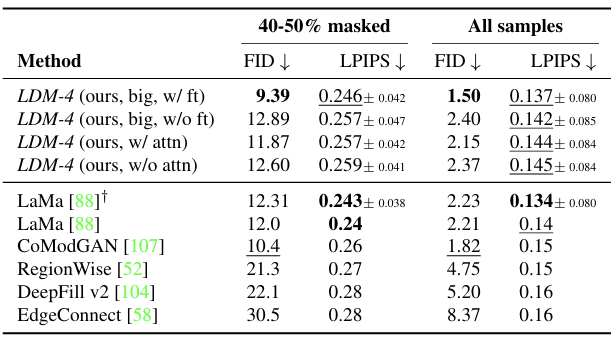
- Places 데이터로 학습·평가 시, 기존 Inpainting 전용 모델(LaMa 등)과 견줄 만한 성능 달성하였다.
- User Study 결과, LDM 기반 결과물이 시각적 일관성을 더 높게 유지한다는 피드백이 확인되었다.
5. Limitations & Societal Impact
- Limitations
- 기존 pixel-based Diffusion Model에 비해 계산 비용이 크게 감소했으나, sampling 속도는 여전히 GAN류보다 느리다.
- 고해상도 초정밀 이미지 생성 시, reconstruction 한계가 존재 (특히 $f=4$ Autoencoder에서 미세 픽셀 정확도 유지가 어려울 수 있음)
- 일부 SR 작업은 이미 어느 정도 한계를 보인다.
- Societal Impact
- 창의적인 응용(예: 예술, 디자인) 가능성과 동시에, deepfake 등 악의적 조작 위험도 존재한다.
- 여성 등 특정 집단이 허위 정보나 이미지 합성의 피해에 더 취약하다.
- 모델이 학습 데이터(민감 정보 포함)를 노출할 가능성이 있으며, 이에 대한 프라이버시·윤리 문제 우려가 있다.
- 딥러닝 모델은 데이터 편향을 그대로 재현·증폭할 위험성이 있으므로, 공정성 및 정확한 분포 이해가 필수적이다.
6. Conclusion
Contributions
- Transformer 기반 접근법들과 달리, 본 연구는 더 높은 차원의 데이터에 대해 더 잘 scaling되며,
- 보다 충실하고 세밀한 재구성을 제공하는 compression 수준에서 작동 가능하고,
- megapixel급 고해상도 합성에도 효율적으로 적용 가능하다.
- unconditional synthesis, inpainting, stochastic super-resolution에서 경쟁력 있는 성능을 달성하였고, 계산 비용을 크게 절감하였다.
- 기존 연구는 encoder/decoder와 score-based prior를 동시에 학습해야 했던 반면, 본 접근법은 두 영역의 균형 조정이 필요 없으며, 재구성 충실도가 매우 높고, latent space의 정규화가 거의 필요 없다.
- Super-resolution, inpainting, semantic synthesis처럼 dense하게 condition된 task에 대해, convolutional 방식으로 적용 가능하며, 1024×1024 해상도의 이미지도 일관성 있게 합성할 수 있다.
- Cross-attention 기반의 일반 목적 conditioning mechanism을 설계하여, multi-modal 학습이 가능하게 하였다. 이를 통해:
- class-conditional
- text-to-image
- layout-to-image 모델도 학습하였다.
- pretrained latent diffusion 모델, autoencoding 모델을 공개하여 다양한 downstream task에서도 재활용 가능하도록 하였다. https://github.com/CompVis/latent-diffusion



