[DDPM] https://arxiv.org/abs/2006.11239
Denoising Diffusion Probabilistic Models
We present high quality image synthesis results using diffusion probabilistic models, a class of latent variable models inspired by considerations from nonequilibrium thermodynamics. Our best results are obtained by training on a weighted variational bound
arxiv.org
본 논문은 기존 Diffusion Model의 기본적인 토대를 바탕으로 매개화를 통해 새로운 최적화 방식을 도입한다. 또한 새롭게 도입한 모델 훈련 및 샘플링 방식이 다른 연구에서 논의된 것과 형태가 유사함을 보인다.
아래의 두 논문을 읽지 않았다면 이해가 어려울 수 있다.
[Diffusion Model 논문리뷰] https://outta.tistory.com/109
[2024-2] 최민서 - Deep Unsupervised Learning using Nonequilibrium Thermodynamics
https://arxiv.org/abs/1503.03585 Deep Unsupervised Learning using Nonequilibrium ThermodynamicsA central problem in machine learning involves modeling complex data-sets using highly flexible families of probability distributions in which learning, samplin
blog.outta.ai
[NCSN 논문리뷰] https://blog.outta.ai/141
[2025-1] 최민서 - Generative Modeling by Estimating Gradients of the Data Distribution
https://arxiv.org/abs/1907.05600 Generative Modeling by Estimating Gradients of the Data DistributionWe introduce a new generative model where samples are produced via Langevin dynamics using gradients of the data distribution estimated with score matchin
blog.outta.ai
1. Introduction
Diffusion Model은 소량의 노이즈를 단계적으로 추가하는 Markov chain의 역과정을 학습하여 초기 노이즈 $X_T$로부터 노이즈가 제거된 원본 데이터 $X_0$를 추출한다. Diffusion Model은 정의가 명확하고 학습이 쉽지만 현재까지의 연구로는 좋은 품질의 이미지를 생성해내지 못한다.
본 논문에서는 Diffusion Model이 좋은 품질의 이미지를 생성해냄을 증명한다. 또한 특정한 매개화를 통하여 Diffusion Model이 훈련과정에서는 DSM(Denoising score matching)과, 샘플링 과정에서는 annealed Langevin dynamics와 유사한 형태를 띠고 있음을 보인다.
2. Background
Diffusion Model의 순방향 Markov kernel $q$와 역방향 Markov kernel $p$는 아래와 같이 정의된다.
$$ q(\mathbf{x}_{1:T} | \mathbf{x}_0) := \prod\limits_{t=1}^{T} q(\mathbf{x}_t | \mathbf{x}_{t-1}) $$
$$ q(\mathbf{x}_t | \mathbf{x}_{t-1}) := \mathcal{N}(\mathbf{x}_t; \sqrt{1-\beta_t}\mathbf{x}_{t-1}, \beta_t \mathbf{I}) $$
$$ p_\theta(\mathbf{x}_{0:T}) := p(\mathbf{x}_T) \prod\limits_{t=1}^{T} p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_t) $$
$$ p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_{t}) := \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t,t), \Sigma_\theta(\mathbf{x}_t,t) ) $$
이 때 임의의 $t$에 대하여 $\mathbf{x}_0$에 대해 $\mathbf{x}_t$를 아래와 같이 샘플링 할 수 있다.
$$ q(\mathbf{x}_t | \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t;\sqrt{\bar{\alpha}_t}\mathbf{x}_0,(1-\bar{\alpha}_t)\mathbf{I}) $$
$$ \alpha_t = 1-\beta_t, \, \bar{\alpha}_t = \prod\limits_{s=1}^{t}\alpha_s$$
학습은 Negative log likelihood의 Variational bound $L$을 최적화시키는 방식으로 진행된다.
$ \mathbb{E}[-\mathrm{log}p_\theta(\mathbf{x}_0)] \leq -\mathrm{log}\mathbb{E}[p_\theta({\mathbf{x}_0})] $
$ = -\mathrm{log}\int p_\theta(\mathbf{x}_0) p_\theta(\mathbf{x}_{1:T} | \mathbf{x}_0) d\mathbf{x}_{1:T} $
$ = -\mathrm{log}\int p_\theta(\mathbf{x}_{0:T}) \frac{q(\mathbf{x}_{1:T} | \mathbf{x}_0)}{q(\mathbf{x}_{1:T} | \mathbf{x}_0)} d\mathbf{x}_{1:T} $
$ = \mathbb{E}_q \left[ -\mathrm{log}\frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} | \mathbf{x}_0)} \right] $
$ = \mathbb{E}_q \left[ -\mathrm{log}p(\mathbf{x}_T) - \sum\limits_{t\geq 1} \mathrm{log}\frac{p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t)}{q(\mathbf{x}_{t} | \mathbf{x}_{t-1})} \right] =:L $
Variational bound $L$을 아래와 같이 변형할 수 있다.
$$ L = \mathbb{E}_q \left[ L_T + \sum\limits_{t>1}L_{t-1} + L_0 \right] $$
$$ \text{where}\; L_T = D_{KL}(q(\mathbf{x}_T | \mathbf{x}_0) || p(\mathbf{x}_T)), \, L_{t-1} = D_{KL} (q(\mathbf{x}_{t-1} | \mathbf{x}_t,\mathbf{x}_0) || p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t)), \, L_0 =-\mathrm{log}p_\theta(\mathbf{x}_0 | \mathbf{x}_1)$$
$p_\theta$가 추정해야 하는 정방향 Markov chain의 역과정 $q(\mathbf{x}_{t-1} | \mathbf{x}_t,\mathbf{x}_0)$은 충분히 작은 $\beta_t$에 대하여 아래와 같이 정규분포로 표현가능하다.
이는 Bayesian rule을 통해 posterior distribution을 계산하면 유도 가능하다.
$$ q(\mathbf{x}_{t-1} | \mathbf{x}_t,\mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1} ; \tilde{\mu}_t (\mathbf{x}_t,\mathbf{x}_0), \bar{\beta}_t \mathbf{I}) $$
$$ \tilde{\mu}_t(\mathbf{x}_t,\mathbf{x}_0) := \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}\mathbf{x}_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{x}_t $$
$$ \bar{\beta}_t := \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\beta_t $$
결국 $L$의 KL divergence들은 정규분포간의 계산이므로 Rao-Blackwellized 방식을 통해 쉽게 계산할 수 있다.
Rao-Blackwellized 방식은 기존의 확률분포에서 표본을 추출하여 값을 계산하는 Monte Carlo 샘플링 방식과 달리 분산이 작거나 더 정교하게 설계된 조건부 확률분포를 만들어 해당 조건부 확률분포에서 표본을 추출하여 값을 계산하는 방식이다. 위 상황에서는 $L_t$가 두 정규분포의 KL divergence이기 때문에 해석적으로 계산이 가능하다. 이는 $q$와 $p$가 적절하게 조건부 확률분포로 설정되었기 때문이며 이를 Rao-Blackwellized 방식을 통해 계산한다고 논문에서 표현한 듯 하다.
3. Diffusion models and denoising autoencoders
section 3에서는 $ L = \mathbb{E}_q \left[ L_T + \sum\limits_{t>1}L_{t-1} + L_0 \right] $의 각 항들을 뜯어보며 Diffusion Model을 구체화한다.
3.1 Forward process and $L_t$
정방향 커널의 분산계수 $\beta_t$는 학습가능한 변수이지만, 본 논문에서는 이를 상수로 고정한다. 따라서 posterior distribution $q$는 학습가능한 파라미터가 없으므로 학습 시 $L_T$를 무시할 수 있다.
3.2 Reverse process and $L_{1:T-1}$
본 섹션에서는 역방향 Markov kernel $p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1};\mu_\theta(\mathbf{x}_t,t), \Sigma_\theta(\mathbf{x}_t,t) )$을 다룬다.
먼저, 분산 $\Sigma_\theta(\mathbf{x}_t,t)$은 시간에 의존하는 상수 $\sigma_t^2\mathbf{I}$로 고정한다. $\sigma_t^2$의 값은 두 가지로 설정할 수 있다.
1. $\sigma_t^2 = \beta_t$
- 이는 $x_0 \sim \mathcal{N}(0,\mathbf{I})$일 때 최적인 설정이다.
- 역방향 과정의 엔트로피의 상한을 의미한다.
2. $\sigma_t^2 = \tilde{\beta}_t = \frac{1-\tilde{\alpha}_{t-1}}{1-\tilde{\alpha}_t}\beta_t$
- 이는 $x_0$가 한 점에 완벽하게 밀집하여 분포되어 있을 때 최적인 설정이다.
- 역방향 과정의 엔트로피의 하한을 의미한다.
위 두 설정은 두가지 상반된 극한에서의 값이다. 실제 데이터 $x_0$는 두 가정의 중간에 있을 것이고 두 분산 설정 모두 실험적으로 비슷한 결과를 보인다.
이제 평균 $\mu_\theta(\mathbf{x}_t,t)$을 나타낼건데, 먼저 특정 매개화를 통해 $L_t$를 변형한다. 역방향 커널 $p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1};\mu_\theta(\mathbf{x}_t,t),\sigma_t^2\mathbf{I})$에 대해 아래와 같이 $L_{t-1}$을 쓸 수 있다.
$$ L_{t-1} = \mathbb{E}_q \left[ \frac{1}{2\sigma_t^2} || \tilde{\mu}_t(\mathbf{x}_t,\mathbf{x}_0) - \mu_\theta(\mathbf{x}_t,t) ||^2 \right] + C $$
두 동일한 분산의 정규분포의 KL divergence는 위와 같이 평균의 차이에 비례하게 나타난다.
위 식에서 볼 수 있듯이 모델 $\mu_\theta$를 훈련시켜 $q(\mathbf{x}_{t-1} | \mathbf{x}_t,\mathbf{x}_0)$의 평균 $\bar{\mu}_t$를 추정하도록 만들면 된다.
식을 한번 더 매개화하여 변형한다. $\epsilon \sim \mathcal{N}(0,\mathbf{I})$에 대하여 $\mathbf{x}_t(\mathbf{x}_0,\epsilon) = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\epsilon $임을 이용한다.
$ L_{t-1} - C = \mathbb{E}_{\mathbf{x}_{0,\epsilon}}\left[ \frac{1}{2\sigma_t^2} \left\Vert \tilde{\mu}_t \left( \mathbf{x}_t(\mathbf{x}_0,\epsilon), \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t(\mathbf{x}_0),\epsilon) - \sqrt{1-\bar{\alpha}_t}\epsilon \right) -\mu_\theta(\mathbf{x}_t(\mathbf{x}_0,\epsilon),t) \right\Vert ^2 \right] $
$ = \mathbb{E}_{\mathbf{x}_{0,\epsilon}} \left[ \frac{1}{2\sigma_t^2} \left\Vert \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t(\mathbf{x}_0,\epsilon) - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon \right) - \mu_\theta(\mathbf{x}_t(\mathbf{x}_0,\epsilon),t) \right\Vert ^2 \right] $
첫번째 수식에 $ \tilde{\mu}_t(\mathbf{x}_t,\mathbf{x}_0) := \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}\mathbf{x}_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{x}_t $을 대입하면 쉽게 두번째 수식을 유도할 수 있다.
$\mu_\theta(\mathbf{x}_t,t)$를 아래와 같이 매개화한다.
$$ \mu_\theta(\mathbf{x}_t,t) = \tilde{\mu}_t \left( \mathbf{x}_t, \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1-\bar{\alpha}_t}\epsilon_\theta(\mathbf{x}_t) )\right) = \frac{1}{\sqrt{\alpha_t}}\left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_\theta(\mathbf{x}_t,t) \right) $$
$\epsilon_\theta$는 $\mathbf{x}_t$와 $t$를 입력으로 받아 $\epsilon$을 추정하는 함수(신경망)이다. 위 매개화를 통해 $L_{t-1}-C$를 아래와 같이 표현 가능하다.
$$ L_{t-1}-C = \mathbb{E}_{\mathbf{x}_{0},\epsilon} \left[ \frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha}_t)} \Vert \epsilon - \epsilon_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\epsilon ,t) \Vert^2 \right] $$
$\mathbf{x}_t(\mathbf{x}_0,\epsilon) = \sqrt{\tilde{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\tilde{\alpha}_t}\epsilon $의 수식을 보면 $t$번째 데이터 $\mathbf{x}_t$는 원본 데이터 $\mathbf{x}_0$에 일정 비율의 노이즈가 더해짐을 확인할 수 있다. 위 수식은 신경망 $\epsilon_\theta$가 노이즈가 더해진 데이터 $\mathbf{x}_t$와 시점 $t$를 입력으로 받아 그 데이터에 더해진 노이즈 $\epsilon$을 추정하도록 설계되어야 함을 시사한다. 이는 $t$에 의존하여 여러 스케일의 노이즈를 추정하는 DSM(Denoising Score Matching)과 일맥상통한다.
이제 샘플링 과정을 알아보자. $\mathbf{x}_{t-1}$은 조건부 확률분포 $p(\mathbf{x}_{t-1} | \mathbf{x}_t)$를 따른다. 즉 $\mathbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}}\left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta(\mathbf{x}_t,t) \right)$를 계산하여 $\mathbf{x}_t$로부터 $\mathbf{x}_{t-1}$을 샘플링할 수 있다. 해당 샘플링 과정은 Langevin dynamics 알고리즘과 매우 유사하며 $\epsilon_\theta$는 데이터의 확률 밀도의 미분값이라고 생각할 수 있다.
section 3.2의 내용을 요약하면 아래와 같다.
- Diffusion Model의 목표는 정방향 커널의 역과정인 $q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)$을 추정하는 신경망을 만드는 것이다.
- Varaitional bound의 매개화를 통해, 위 목표는 정규분포 $q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)$의 평균을 추정하거나 노이즈 $\epsilon$을 추정하는 두가지 방식 중 하나를 이용하면 달성 가능하다.
- 특히 $\epsilon$을 추정하는 신경망을 이용할 때, 학습 과정은 DSM과 유사하며, 샘플링 과정은 Langevin dynamics와 유사함을 발견했다.
3.3 Data scaling, reverse process decoder, and $L_0$
신경망 $p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t)$는 연속적인 데이터 $\mathbf{x}_t$를 입력으로 받아 연속적인 데이터 $\mathbf{x}_{t-1}$을 출력한다. 하지만 $L_0 = -\mathrm{log}p_\theta(\mathbf{x}_0|\mathbf{x}_1)$가 정확하게 측정되기 위해서는 최종적으로 생성되는 데이터인 $\mathbf{x}_0$가 이산 데이터이어야만 한다.
따라서 역방향 과정의 마지막 디코더인 $p_\theta(\mathbf{x}_0|\mathbf{x}_1)$가 아래와 같이 연속 데이터를 이산 데이터로 매핑하도록 설계한다. 아래 수식은 기존 디코더 $\mathcal{N}(\mathbf{x}_0;\mu_\theta(\mathbf{x}_1,1),\sigma_1^2\mathbf{I})$를 참고한다.
$$ p_\theta(\mathbf{x}_0 | \mathbf{x}_1) = \prod\limits_{i=1}^{D} \int_{\delta-(x_0^i)}^{ \delta+(x_0^i)} \mathcal{N}(x;\mu_\theta^i(\mathbf{x}_1,1),\sigma_1^2)dx $$
$$ \delta_+(x) = \begin{cases} \infty & \text{if} \; x=1 \\ x+\frac{1}{255} & \text{if} \; x<1 \end{cases} $$
$$ \delta_-(x) = \begin{cases} -\infty & \text{if} \; x=-1 \\ x-\frac{1}{255} & \text{if} \; x>-1 \end{cases} $$
$D$는 데이터의 차원, $i$는 차원의 번호를 나타내는 윗첨자이다.
위 수식에서 볼 수 있듯이 디코더 $p_\theta(\mathbf{x}_0|\mathbf{x}_1)$는 $\mathbf{x}_0$의 확률 질량을 $\pm\frac{1}{255}$ 구간에서의 각 차원의 확률밀도의 곱으로 정의한다.
정의에 따르면 확률밀도(질량)함수 $p_\theta(\mathbf{x}_0|\mathbf{x}_1)$는 모든 $\mathbf{x}$에 대해 정의될 수 있어 연속확률변수에 대한 확률밀도함수라고 생각할 수 있지만, 논문에서는 $-1,-\frac{253}{255},\dots,\frac{253}{255},1$에서 이산적으로 정의된 확률변수에 대한 확률질량함수라고 생각하는 듯 하다.
3.4 Simplified training objective
section 3.2에서 매개화를 통해 variational bound를 아래와 같이 변형했다.
$$ L_{t-1}-C = \mathbb{E}_{\mathbf{x}_{0},\epsilon} \left[ \frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha}_t)} \Vert \epsilon - \epsilon_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\epsilon ,t) \Vert^2 \right] $$
아래의 단순화한 variational bound를 살펴보자.
$$ L_{simple}(\theta) := \mathbb{E}_{t,\mathbf{x}_0,\epsilon} \left[ \Vert \epsilon - \epsilon_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\epsilon ,t) \Vert^2 \right] $$
가중치가 없는 버전의 $L$ 수식이라 생각하면 된다. 이는 $t$에 의존하는 denoising score matching model인 NCSN과 유사한 형태를 띤다.
$L_{simple}$은 작은 $t$에서는 노이즈의 크기가 작기 때문에 이 때의 loss 값을 down-weight한다. 이는 노이즈가 큰 구간, 즉 학습이 어려운 구간에서의 loss 값을 상대적으로 크게 만들어 학습의 효율을 높인다. 자세한 과정은 section 4에서 후술한다.
결과적으로 학습 및 샘플링 알고리즘은 아래와 같이 구현된다.

4. Experiments
실험에서 $T=1000$으로 설정되어 이전 Diffusion Model 연구에서의 세팅과 똑같이 설정했다. 또한 $\beta_1 = 10^{-4}$부터 $\beta_T = 0.02$까지 선형적으로 증가하도록 설정했다. $\beta_t$ 값은 $[-1,1]$에서 정의된 데이터의 스케일에 비해 작은 값으로 설정되었다.
4.1 Sample quality
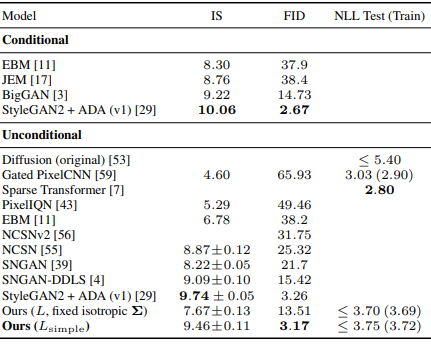
위 표에서 볼 수 있듯이 논문의 Diffusion Model이 다른 생성형 모델보다 좋은 IS, FID 점수를 얻었다.
또한 원본 variational bound를 이용했을 때보다 단순화된 $L$을 이용했을 때, 학습은 비교적 잘 안되었지만 더 좋은 품질의 이미지를 생성함을 실험적으로 확인했다.
4.2 Reverse process parameterization and training objective ablation
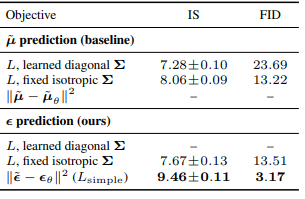
위 표는 section 3.2에서 논의된 학습 방식들의 성능을 비교한다. 범위 밖의 낮은 점수는 빈칸으로 표시했다.
$\tilde{\mu}$를 추정하는 방식의 경우 $\Sigma$도 학습에 포함시키는 경우 점수가 낮아졌다. 또한 단순화된 가중치 없는 손실값을 사용할 때 학습이 잘 되지 않았다. 반면 $\epsilon$을 추정하는 방식의 경우 가중치 없는 $L_{simple}$을 사용하여 학습시켰을 때 다른 모든 방식보다 성능이 좋음을 확인할 수 있었다.
즉 본 논문에서 제시한 $\epsilon$을 추정하는 방식은 수식적으로 단순명료할 뿐만 아니라 다른 학습 방식에 비해 좋은 성능을 보임 또한 검증되었다.
4.3 Progressive coding
본 섹션에서는 Diffusion Model을 정보 이론의 관점에서 설명한다. 아래 용어들을 숙지하고 가면 좋다.
Rate : 데이터를 전송하기 위해 필요한 비트 양
Distortion : 원본 데이터를 복원했을 때 오차의 값
Rate와 Distortion은 trade-off 관계이다. Rate가 낮으면 전송에 쓰이는 비트가 적어 복원이 어려워지고 Distortion이 커진다. 작은 Distortion 값을 얻기 위해서는 충분히 큰 Rate이 필요하다.
Progressive lossy compression
$L = \sum\limits_{t=0}^T$에서 $L_1+\dots+L_T$를 rate, $L_0$를 distortion이라 볼 수 있다. CIFAR10 데이터셋으로 훈련시킨 결과, 모델의 rate 값은 1.78bits/dim, distortion 값은 1.97bits/dim이 나온다. 해당 distortion 값은 [0,255] 스케일에서 RMSE 0.95의 값으로 사람 눈으로 구별할 수 없는 미세한 오류이다. 절반 이상(1.97bits/dim)의 비트가 눈에 구별되지 않는 미세한 오류(RMSE 0.95)를 없애는 데 사용된다. 이에 논문에서는 Diffusion Model이 lossy compression에 매우 적합한 inductive bias를 가진다고 말한다.
아래 그래프를 통해 이 현상에 대해 더 자세하게 알아보자.
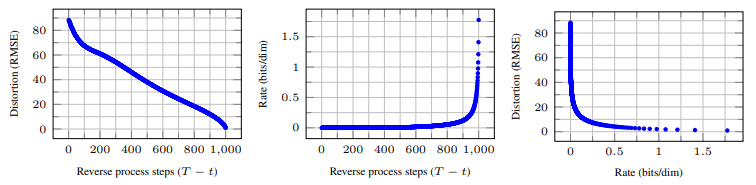
두번째 그래프에서 수행하는 step의 수($T-t$)가 커질수록 Rate 값이 증가함을 확인할 수 있다. 특히 노이즈의 크기가 작은 구간($T-t>800$)에서 많은 비트가 쓰이는데 이는 미세한 오류를 없애는데 많은 비트가 사용된다는 위의 설명과 일맥상통한다.
세번째 그래프에서는 Rate와 Distortion의 trade-off를 확인할 수 있다. 특히 Rate 값이 작은 구간에서 Distortion이 급격하게 작아지는데, 이는 Diffusion Model의 초반 kernel들이 큰 오류를 없애고 이후 kernel들은 미세한 오류를 없애는데 사용되어 이에 많은 비트가 사용된다.
Progressive generation

위 그림은 각 time step에서 $x_0$를 복원한 결과를 나타낸다. 이미지의 큰 특징이 먼저 시각화되고 이후 미세한 디테일들이 추가됨을 확인할 수 있다.

위 그림은 고정된 $\mathbf{x}_t$로부터 어떻게 랜덤한 원본 이미지 $\mathbf{x}_0$가 생성되는지 보여준다. $t$ 값이 클수록 큰 시각적 특징만이 보존되며 $t$값이 작아질수록 미세한 특징 외에 거의 유사한 이미지들이 생성된다.
4.4 Interpolation
Diffusion Model은 두 이미지를 자연스럽게 결합(interpolate)하는데에도 유용하다. 서로 다른 두 이미지 $\mathbf{x}_0$와 $\mathbf{x}_0^\prime$에 각각 정방향 확산을 진행하여 잠재변수 $\mathbf{x}_t$와 $\mathbf{x}_t^\prime$를 얻는다. 그 후 두 잠재변수를 $\lambda\mathbf{x}_t + (1-\lambda)\mathbf{x}_t^\prime$와 같이 interpolate한다. 이후 interpolate한 잠재변수를 역방향 복원을 진행하면 자연스럽게 interpolate된 이미지를 생성할 수 있다.

위 그림은 $\lambda$의 값에 따라 interpolate된 이미지들을 보여준다. 안경을 제외한 여러 신체적 특성이 자연스럽게 결합되었음을 확인할 수 있다.
5. Conclusion
본 논문에서는 Diffusion Model을 이용해 좋은 품질의 이미지를 생성할 수 있음을 밝혔다. 특히 매개화를 통해, 이미지와 시점을 입력으로 받아 그 이미지에 낀 노이즈인 $\epsilon$을 추정하도록 신경망을 설계했다. 정의된 loss는 수식이 간단하여 구조화하기 쉽고 훈련도 어렵지 않다는 장점이 있으며 뿐만 아니라 기존의 생성형 모델보다 좋은 성능을 보인다.




