1. 차원 축소란?
차원의 저주 (Curse of Dimension)는 입력된 데이터의 수보다 데이터의 차원이 더 큰 경우 발생하는 문제입니다. 예를 들어 100개의 데이터 그리고 각 데이터의 차원은 500인 상황이 발생하게 되면 백터 공간의 차원이 무수히 커지고 데이터는 여기저기 흩뿌려지게 됩니다. 모델의 복잡도가 증가하고 예측 성능이 낮아지게 됩니다.

차원 축소는 이러한 고차원 데이터를 저차원으로 변환하여 계산 효율을 높이고, 노이즈를 제거하며, 중요한 정보를 유지하면서도 이해하기 쉽게 만들어주는 중요한 기법입니다.
- Feature Selection : 특정 Feature에 종속성이 강한 불필요한 Feature 제거 우리 목적의 불필요한 Feature를 날림
- Feature Extraction : 기존 Feautre를 저차원의 중요 Feature로 압축해서 추출하여 새로운 Feauture를 만드는 것
차원 축소의 주요 기법인 PCA, SVD, LSA, LDA, MF에 대해 설명하도록 하겠습니다.
2.1 주성분 분석 (PCA)
PCA는 고차원 데이터를 저 차원으로 축소하는 차원 축소 기법 중 하나로, 데이터의 분산을 가장 잘 설명하는 방향(주성분)을 찾아내어 데이터를 투영합니다. 이는 데이터의 중요한 특징을 유지하면서도 데이터의 크기를 줄이는 데 효과적입니다.
- PCA의 목표는 점들의 분산이 최대로 본존 될 수 있는 축을 찾는 것이고 이를 PC(주성분)이라고 한다.
- PC를 찾기 위해서는 Covariance Matrix(공분산 행렬)에서 Eigenvalue가 가장 큰 값인 Eigenvector(고유 벡터)를 찾아야한다.
- 데이터를 PC에 투영시켜서 차원을 축소시킨다

2.2 특이값 분해 (SVD)
SVD (Singular Value Decomposition)는 $m\times n$ 행렬을 3개의 행렬로 분해하는 기법이다. 고유값분해 (Eigenvalue Decomposition) 와 비슷하지만, 고유값 분해는 정사각 행렬에만 사용 가능한 반면, 특이값 분해는 직사각 행렬일 때도 사용 가능해서 활용도가 높습니다.
$$ A= U \Sigma V^T $$
- $A: m×n$ 크기의 원본 행렬
- $U: m×m$ 크기의 직교 행렬로, 행 방향 특이 벡터를 담고 있습니다. (스켕일링 데이터를 최종적으로 회전)
- $\Sigma: m×n$ 크기의 대각 행렬로, 특이값(Singular Values)을 표현합니다. (데이터를 스케일링)
- $V^T: n×n$ 크기의 직교 행렬로, 열 방향 특이 벡터를 담고 있습니다. (데이터를 회전)
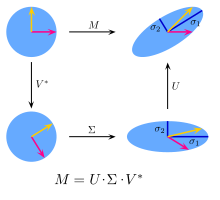
SVD의 계산과정 :
- $A^TA$와 $A^TA$계산
- $A^TA$의 고윳값 구한 후, 정규화된 고유백터 $V$도출
- 특이값 $\Sigma$ 구성 (특이값은 고윳갑의 제곱근)
- $AA^T$의 고윳값 구한 후, 정규화된 고유백터 $U$도출
→ SVD는 $\Sigma$의 상위 $k$개의 특이값만 남기고 나머지를 제거하여 저 차원 표현을 생성할 수 있습니다.
2.3 잠재 의미 분석 (LSA)
LSA (Latent Semantic Analysis)는 문서와 단어가 벡터로 표현될 때 잠재 의미 공간(Latent Semantic Space)을 정의함으로써 텍스트에서 의미를 추출하는 방법입니다. 이는 풀 SVD에서 나온 3개의 행렬에서 일부 벡터를 삭제시킨 절단된 SVD(truncated SVD)를 사용하게 된다.
- 예를 들어, n개의 문서에서 중복을 제거한 단어들의 총개수를 m이라고 가정합시다. 이를 기반으로 문서-단어 행렬(DTM, Document-Term Matrix) A를 생성하면, A는 m×n 크기를 갖는 행렬이 됩니다.

- 이제 이 행렬 A를 특이값 분해(SVD, Singular Value Decomposition)를 통해 분해하면 다음과 같이 나타낼 수 있습니다.
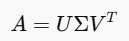
- 이와 동시에 $U$와 $V^T$ 행렬에서도 $k$에 대응하는 부분만 남겨 $U_k$와 $V_K^T$를 생성하고 새로운 행렬 $A_k$를 계산할 수 있습니다.
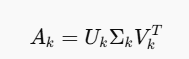
- 행렬 $A_k$는 원본 행렬 $A$와 동일한 크기를 유지하지만, 불필요한 토픽은 제거되고 주요 토픽(문서의 잠재 의미, 중요한 단어와 주제)만 남아 있는 상태가 됩니다. 다시 말해, $A$는 문서의 원본 정보를 포함하지만 노이즈와 불필요한 정보도 포함되어 있는 반면, $A_k$는 중요한 정보만 추출된 행렬입니다.
2.4 선형판별분석 (Linear Discriminant Analysis, LDA)
LDA 또한 PCA와 마찬가지로 차원 축소를 하는 방법 중 하나이다. PCA처럼 입력 데이터 세트를 저 차원 공간에 투영해 차원을 축소하는 기법. 중요한 차이는 LDA는 지도학습의 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원 축소된다는 것입니다.

- PCA는 입력 데이터의 변동성의 가장 큰 축을 찾았지만, LDA는 입력 데이터의 결정값 클래스를 최대한 분리할 수 있는 축을 찾음.
LDA 차원 축소 방식
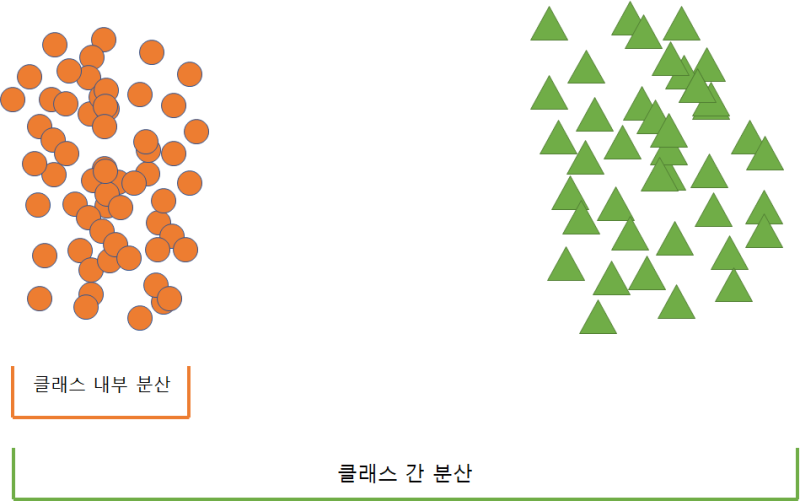
특정 공간상에서 클래스 분리를 최대화하는 축을 찾기 위해 클래스 간 분산은 최대한 크게, 클래스 내 분산은 최대한 작게 만들어 내는 축을 찾아서 축소시킵니다.
LDA의 과정
- 클래스 내부와 클래스 간 분산 행렬을 구하고, 이 두 개의 행렬은 입력 데이터의 결정 값 클래스별로 개별 Feature의 평균 벡터를 기반으로 구함
- 클래스 내부 분산 행렬을 SW, 클래스 간 분상 행렬을 SB라고 하면, 다음 식으로 두 행렬을 고유벡터로 분해할 수 있음
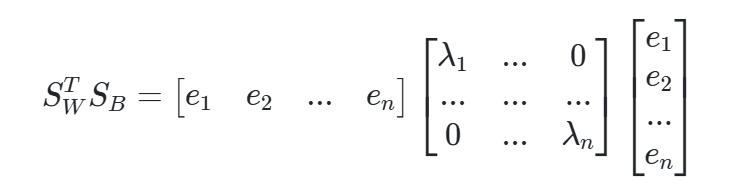
3. 고윳값이 가장 큰 순으로 K개(LDA변환 차수만큼) 추출
4. 고윳값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력 데이터를 변환
LDA와 PCA차이
다시 정리하자면, PCA는 입력된 데이터의 공분산행렬을 구해서 고유벡터와 고윳값을 구해 차원을 축소시키지만, LDA는 클래스 내부 분산과 클래스 간 분산 행렬을 생성한 다음 이들의 고유벡터와 고유값을 구해 축소시킵니다. 데이터의 공분산행렬을 쓸지, 클래스와 관련된 분산을 쓰는지에 대한 차이라고 생각하면 될 것 같습니다.
2.5 행렬 분해 (MF)
MF (Matrix Factorization)는 행렬을 두 개의 저 차원 행렬로 분해하는 기법입니다. 사용자-아이템 행렬(User-Item Matrix)을 저 차원으로 분해하여 잠재 요인(latent factor)을 추출하는 데 사용됩니다. SVD와 개념이 유사하지만, 관측된 평점만 모델링에 사용하고 관측되지 않은 평점을 예측하는 일반적인 모델을 만드는 것이 목표.
- 수식으로 보면 다음과 같다.
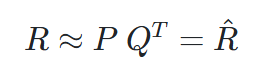
- 즉 Rating Matrix를 P와 Q로 분해하여 R과 최대한 유사한 R^을 추론 하는 것이다.
MF과정
- 이제 행렬 분해를 통해 결측치를 채우고 잠재 요인을 분석할 수 있습니다. 예를 들어 R 행렬은 4x6 크기의 행렬이고 4x2와 2x6 크기의 행렬로 분해된다고 가정합시다.
R = P * Q

- 그러면 이때, "2"는 잠재요소(latent factor)의 개수를 의미합니다. 즉, 차원을 축소할 때 목표로 하는 잠재요소의 수를 지정한 것입니다.
- 왼쪽 행렬 (W): 유저수(4) x Latent Feature 수 (2)
- 원본 행(row)과 새로운 열(column, 잠재요소)을 포함하고 있습니다. 이는 "원본 행에 대해 잠재요소의 값이 어떻게 되는가?"를 나타냅니다.
- 오른쪽 행렬 (H): Latent Feature 수 (2) x 아이템수(6)
- 원본 열(column)과 새로운 행(row, 잠재요소)을 포함하고 있습니다. 이는 "잠재요소가 원본 행렬의 어떤 요소로 구성되어 있는가?"를 보여줍니다.
- 그리고 Objective Function을 정의하고 정의한 R과 R^을 이용해서 최적화 문제를 푸는 것이다.

2.6 Non-negative Matrix Factorization(NMF)
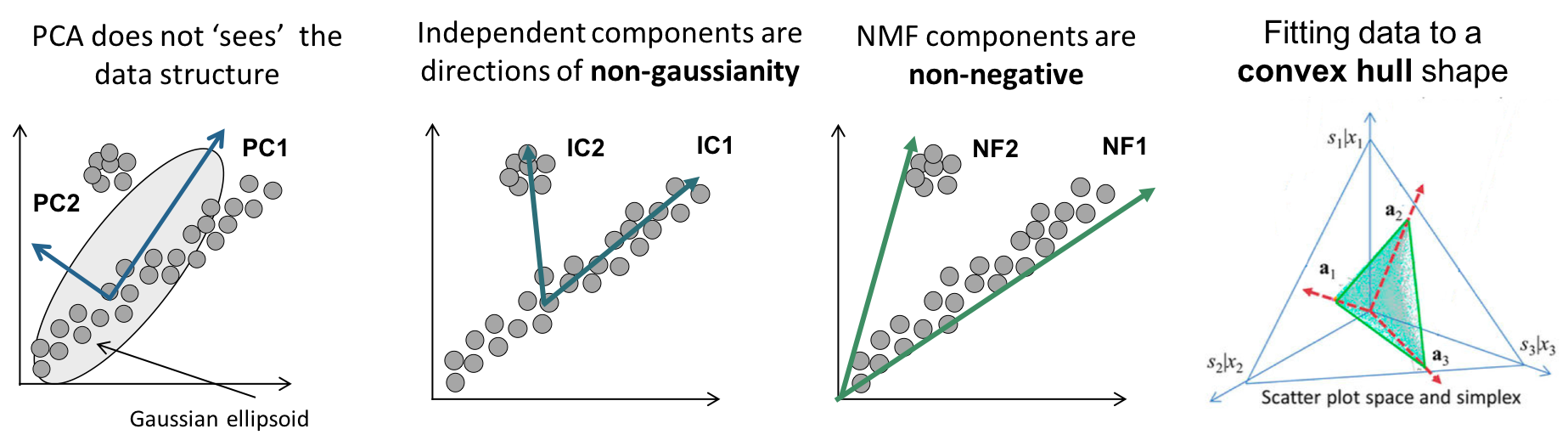
MF에서는 NMF가 있는데 이는 음수를 포함하지 않는 행렬의 행렬분해를 말합니다. 원본 행렬의 값들이 모두 양수면, 간단하게 행렬이 분해될 수 있습니다. 양수일 때 만 쓸 수 있는 제약조건이 있는데 데이터가 모두 양수일때 PCA와 SVD보다 NMF가 더 잘 축소를 시킨다고 합니다.
'Miscellaneous' 카테고리의 다른 글
| [2024-2] 박경태 - deeplearning: Probability and Information Theory (1) | 2025.01.03 |
|---|---|
| [2024-2] 박경태 - deeplearning: Linear Algebra (0) | 2024.12.31 |
| [2024-2] 김영중 - Learning representations by back-propagating errors (2) | 2024.12.08 |
| [2024-1] 김동한 - A Short Introduction to Boosting (0) | 2024.05.21 |
| [2024-1] 박지연 - Rectified Linear Units(ReLU) Improve Restricted Boltzmann Machines (0) | 2024.05.12 |


