Paper Information
- 논문링크: https://arxiv.org/pdf/1609.02907
- 게재 컨퍼런스 : International Conference on Learning Representations(ICLR) 2017
- 저자: *Thomas N. Kipf, Max Welling from University of Amsterdam
그래프
들어가기에 앞서 그래프가 생소한 분들을 위해 개념을 소개합니다.
그래프란? 객체들의 집합이며, 객체의 일부는 서로 관련이 있음. 그래프는 정점(Vertices, Nodes)와 그 정점들을 잇는 간선(Edges)으로 구성됨. 객체 간 관계를 모델링할 때 그래프를 사용함.
"A graph is a structure consisting of a set of objects where some pairs of the objects are in some sense 'related'.
The objects are represented by abstractions called vertices and each of the related pairs of vertices is called an edge."
- 출처: 위키피디아
예시) Scene graph, Knowledge graph, Molecules, Social graphs, Communication graphs, Citation Networks


[Citation Graph
Visually explore diversified yet relevant scientific resources
citationgraph.org](https://citationgraph.org)
그래프를 표현하는 방법
1. List of edges

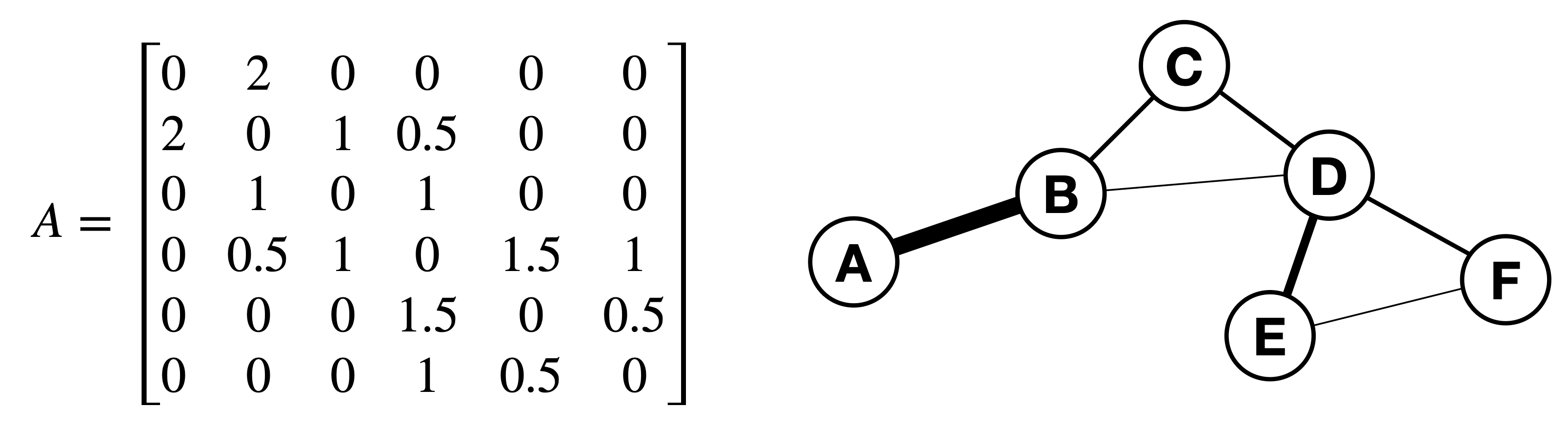
2. Adjacency Matrix(인접행렬)✅
- 간선이 연결되어 있는 노드는 1, 아닌 노드는 0

그래프의 특징
1. Directed or undirected graphs
객체(정점)간의 관계(간선)가 양방향일수도, 단방향일 수도 있음.

2. Weighted or unweighted edges
- 정점 간 관계의 중요도에 따라 간선마다 모두 같은 가중치를 쓸 수도, 다른 가중치를 쓸 수도 있음.
3. Node(Vertice) features
- 정점마다 다른 특성을 가질 수도 있음.

Graph Neural Network의 목표
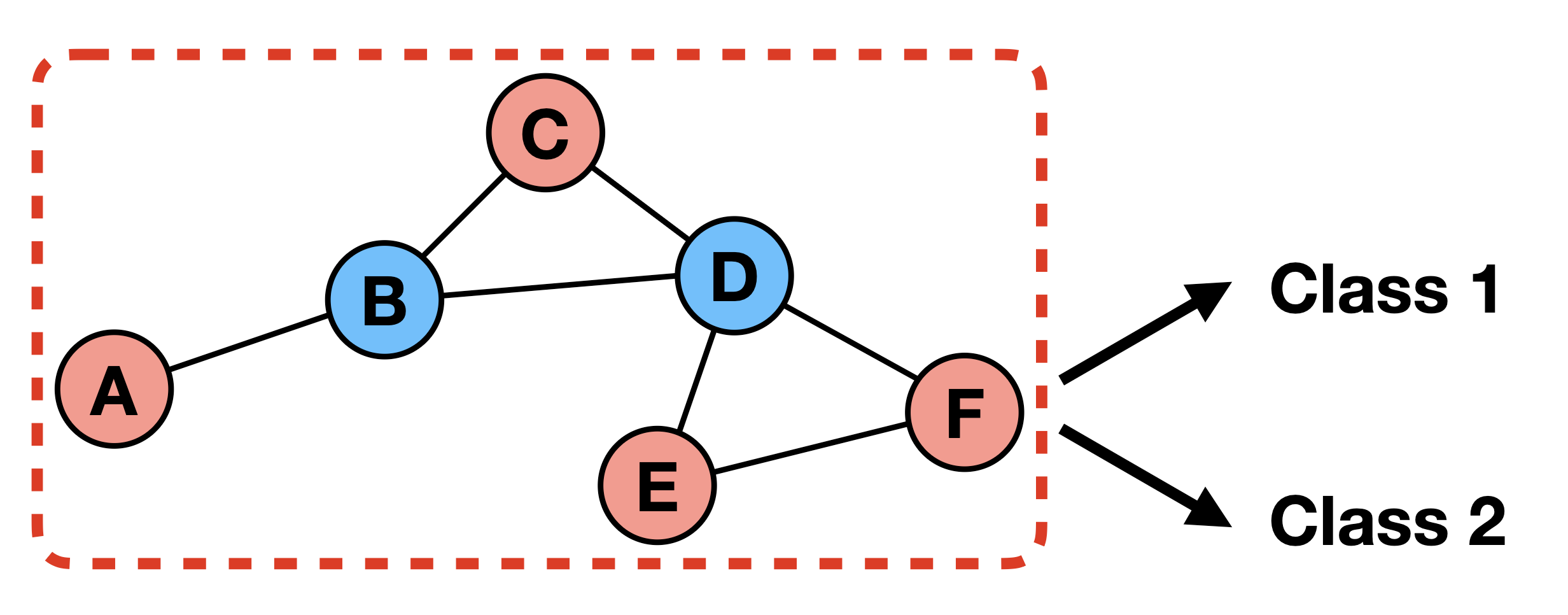
1. Node level prediction✅
- 해당 노드가 어떤 값, 특성을 가질지 예측하는 문제

2. Edge level prediction
- 특정 노드 간 관계(엣지)가 존재할지, 존재한다면 어떤 가중치를 가지고 존재할지 예측하는 문제

3. Graph level prediction
- 모델링된 그래프를 보고 해당 그래프가 어떤 특성을 나타낼지 예측하는 문제
Abstract
- 목표: 그래프 구조의 데이터에 semi-supervised classification을 하는 것
- Spectral Graph Convolutions의 localized first-order approximation을 이용해서 컨볼루션 아키텍처 구성.
1 INTRODUCTION
문제 세팅
- 노드의 라벨이 한정적으로 존재하는 그래프에서 노드의 특징을 분류하는 문제 -> Node level prediction in a semi-supervised manner
기존에 풀던 방식
- Explicit한 형태의 그래프 라플라시안 정규화를 통해서 라벨을 스무딩 시켜 semi-supervised learning 시도.
* 라플라시안 정규화란 서로 연결된 노드는 비슷한 값을 가질 것이다라는 가정에 따른 정규화.
* 라벨 스무딩이란 라벨을 0/1로만 구분하는 것이 아니라 확률을 분산시켜서 보다 generalize한 상태. 노이즈에 강해져서 예측 결과가 더 robsut해짐.

이 방식의 문제: 그래프 엣지들이 항상 노드의 유사도를 반영하지 않을 수도 있기 때문에 모델 표현력을 제한할 수 있음. 그리고 edge는 노드 유사도 말고도 다른 정보를 담고 있을 수 있음.
이 페이퍼에서 시도하는 방식
- 그래프 구조에 Neural Network를 직접적으로 이용하고, explicit한 정규화 사용을 피함.
- 라벨이 있든 없든 모든 노드의 피처와 adjacency matrix(인접행렬)를 신경망에 forward하고, 대신 target supervised loss는 라벨이 있는 노드에 대해서만 계산을 해서 다시 back propagation. 이 과정을 통해서 라벨이 없는 노드들도 gradient를 받을 수 있게 되는 구조.
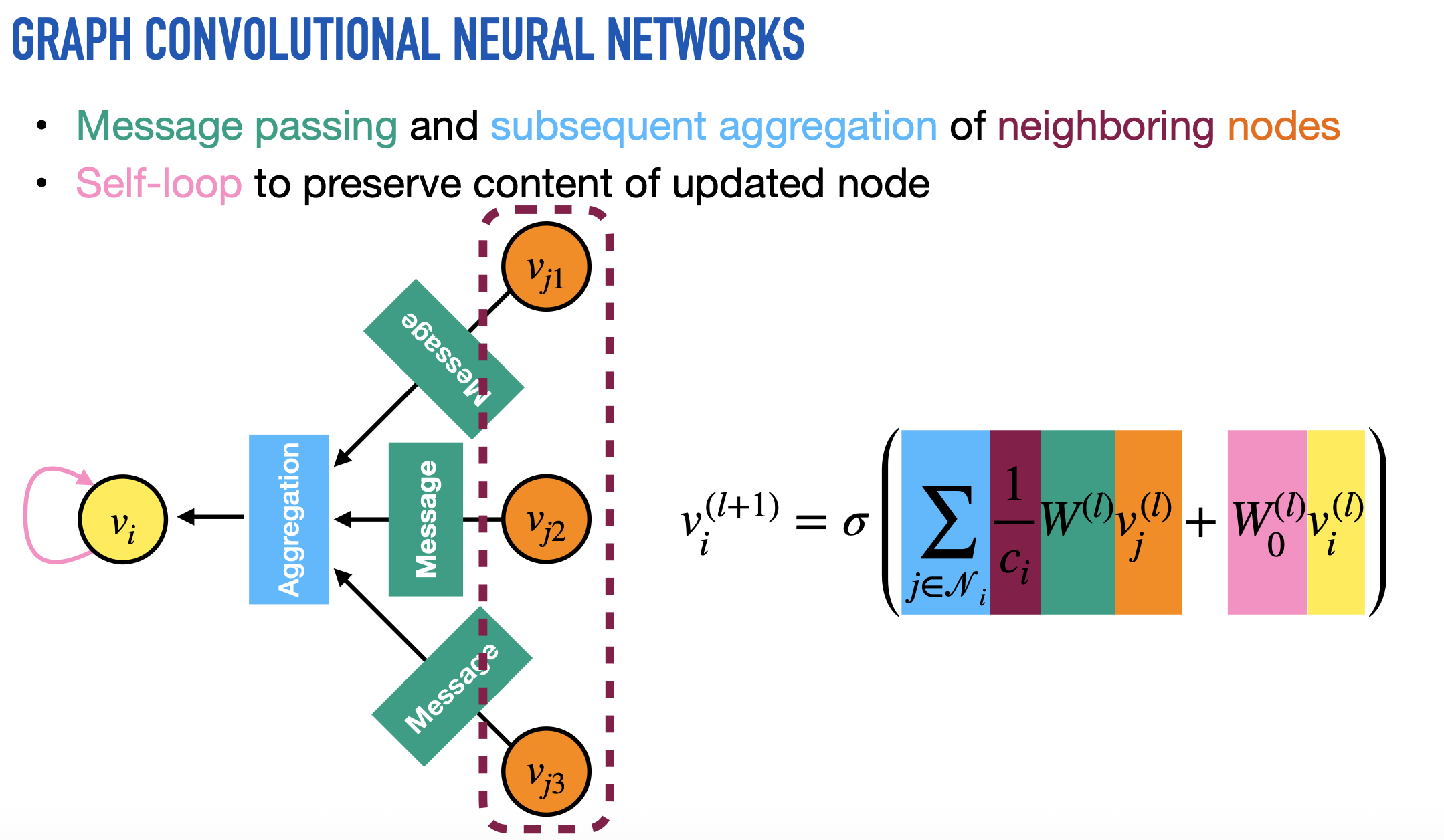
- 이름이 Graph "Convolution" Networks인 이유도 이웃들의 정보를 모아서 새로운 값을 만드는 연산이기 때문임.
2 FAST APPROXIMATE CONVOLUTIONS ON GRAPHS
다음 layer-wise propagation rule을 따르는 Multi-layer GCN 사용
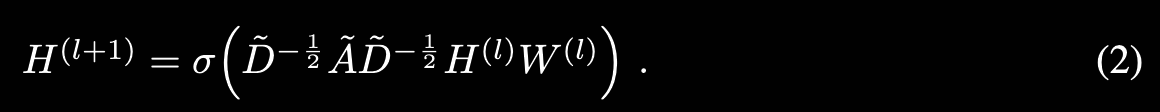
$\tilde{A} = A + I_N$ Undirected graph G의 인접행렬에 self-connections을 더한 형태.
$\tilde{D} _{ii} = \sum \tilde{A} _{ij}$ Degree 행렬. i 노드가 다른 노드와 얼마나 연결되어 있는지 그 수의 합. 대각행렬로 표현됨. Degree 행렬의 역행렬을 A에 곱하는 이유는 값을 Normalize 하기 위해서임. 그냥 A를 Weight에 곱하면 이웃이 많은 노드는 feature가 지나치게 커지고, 이웃이 적은 노드는 feature가 작음. 그런데 이때 A의 양쪽에 역행렬의 절반씩을 곱하는 이유는 행렬의 symmetric을 유지하고, spectral decomposition을 가능하게 만들기 때문.
$\sigma$ 는 activation function.
$H^{l}$는 l-th layer의 activations 값.
2.1 Spectral Graph Convolutions
그래프는 노드 간 우선 순위가 없고, 위치 관계가 정의되지 않았기 때문에 이미지처럼 컨볼루션을 바로 수행할 수 없다. 따라서 그래프의 주파수(푸리에) 도메인에서 컨볼루션을 수행해야 함.

그래프에서의 스펙트럴 컨볼루션을 다음과 같이 정의.
각 노드의 시그널 $x$와 푸리에 영역에서 정의된 필터 $g_\theta$의 곱으로 표현됨.
$U$는 정규화된 그래프 라플라시안($L=I_N - D^{-1/2}AD^{-1/2}=U\Lambda U^T$)의 고유벡터, $\Lambda$는 정규화된 그래프 라플라시안의 고유값.
그러나 큰 그래프에서 $L$의 고유분해 계산은 비싸고, 고유벡터 $U$와의 곱은 O(N^2)가 소모된다는 한계점 존재.
그래서 고유분해를 하지 않고도 spectral filter를 사용할 수 있도록 Chebyshev 다항식으로 근사함.

Chebyshev 다항식은 재귀식.
$T_0(x)=1$
$T_1(x)=x$
$T_k(x)=2xT_{k-1}(x)-T_{k-2}(x)$
이 필터를 다시 spectral convolution 식에 넣으면 다음과 같은 형태가 됨.
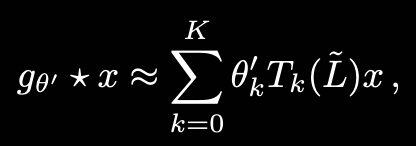
여기서 원래 $L=I_N - D^{-1/2}AD^{-1/2}=U\Lambda U^T$였던 라플라시안의 스케일을 재조정해서 Chebyshev 다항식에서 잘 근사가 되도록 만듦. (Chebyshev 다항식은 주파수 범위 [-1, 1] 구간에서 근사가 잘 됨. 기존 라플라시안은 [0, 2] 범위.)
$\tilde{L} = \frac{2}{\lambda_{max}} L - I$
위 식은 라플라시안 K-th order 다항식이기 때문에 K-localized 되었다고 말할 수 있음.(K step 떨어진 이웃까지만 영향을 주고 받음)
$T_k(\tilde{L})$는 L의 k차 polynomial이기 때문.
근사한 식의 계산 복잡도는 $O(|\epsilon|)$. 엣지의 수와 비례.
2.2 Layer-Wise Linear Model
이제 이 컨볼루션 레이어들을 쌓아서 Neural Network Model을 만들 수 있음.
논문에서 계산의 간단성을 위해서 K = 1로 둠. (한 스텝 떨어져 있는 이웃 정보까지만 보도록)
$g_\theta * x ≈ \theta_0 x + \theta_1 \tilde{L} x$
$\lambda_{max} = 2$로 두면, 위에 리스케일링 했던 이 식($\tilde{L} = \frac{2}{\lambda_{max}} L - I$)이 $\tilde{L} = L-I$으로 변함.

이 식에서는 파라미터 두 개 $\theta _0', \theta _1'$가 나오는데, 실전에서는 파라미터의 수를 줄이는 것이 overfitting을 줄이고, 연산량을 줄일 수 있기 때문에 단일 파라미터로 변환하여 사용함. $\theta = \theta _0' = - \theta _1'$

그런데, $I_N+D^{-1/2}AD^{-1/2}$는 고유값의 범위가 [0, 2]가 되므로 반복해서 사용할 경우 exploding/vanishing gradients 문제가 발생할 수 있음. 따라서 renormalization trick을 사용.

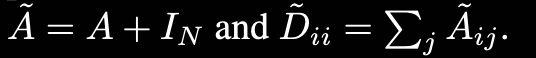
다시 식을 generalize 하면 다음과 같은 형태
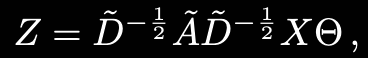
이 operation은 $O(|\epsilon|FC)$가 됨. F는 필터의 개수, C는 채널 개수.
3 SEMI-SUPERVISED NODE CLASSIFICATION
3.1 Example
Semi-supervised node classification을 위한 2 layer GCN 사용.
전처리로 다음 값을 미리 계산.

이후 모델에 값을 넣어 forward.

라벨이 있는 예제들에 대해서는 Cross-entropy error 계산

5 EXPERIMENTS
Citation networks에서 documentation classification, Knowleged graph에서 추출한 bipartite graph에서 entity classification, 그래프 전파 모델 평가, 랜덤 그래프에 대한 실행 시간 분석 실험.
5.1 Datasets

5.2 Experimental Set-up
- 2 Layer GCN
- Test on 1,000 labeled examples
- Maximum 200 epochs
- Learning rate 0.01
- Early stopping with a window size 10
5.3 Baselines
- Label Propagation(LP)
- Semi-supervised embedding (SemiEmb)
- Manifold Regularization(ManiReg)
- Skip-gram based graph embeddings(DeepWalk)
+ Iterative Classification Algorithms
6 RESULTS



7 LIMITATIONS AND FUTURE WORK
1. Memory requirment: 큰 그래프는 GPU 메모리에 올릴 수 없음. 대신 CPU로 훈련할 수 있기는 함. 더 큰 그래프에 대해서는 다른 근사가 필요.
2. Directed edges and edge features: edge feature와 directed graph를 지원하지 않음.
3. Limiting assumptions: 근사를 사용하면서 self connection을 추가적으로 더했는데, 이 self connection의 중요도와 이웃들과의 연결의 중요도를 같게 두는 것이 항상 좋은 결과를 낸 것은 아니었음. 추가적인 파라미터 튜닝이 필요할 듯.
8 CONCLUSION
그래프 구조의 데이터에 Semi-supervised classification이 가능하도록 함. Spectral convolution의 First-order approximation을 이용해서 효율적으로 layer-wise propagation rule을 만들었음. 실험 결과로 GCN이 효율적으로 좋은 성능을 낸다는 것을 확인한 논문.
