ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION (ICLR, 2015) - Adam
DECOUPLED WEIGHT DECAY REGULARIZATION (ICLR, 2019) - AdamW
An overview of gradient descent optimization algorithms (2017) - Momentum, RMSProp 참고
1️⃣Momentum
개념
기본적인 SGD(확률적 경사 하강법)가 경사를 따라 조금씩 내려가는 방식이라면, Momentum은 물리학의 관성 개념을 도입한 방식이다. 공이 언덕을 굴러 내려갈 때 중력 가속도를 받아 속도가 점점 빨라지는 것처럼, 현재의 기울기뿐만 아니라 과거의 속도를 반영하여 파라미터를 업데이트한다.
해결하고자 한 문제: 진동(Oscillation)과 느린 학습
SGD는 협곡(Ravine) 같은 지형(한쪽 차원은 경사가 가파르고 다른 쪽은 완만한 지형)에서 심각한 문제를 겪는다.
- 가파른 경사 방향으로는 급격하게 움직이고 완만한 방향으로는 더디게 움직인다.
- 목표 지점(Local Optima)을 향해 똑바로 가지 못하고 지그재그로 진동하는 현상이 발생하여 수렴 속도가 매우 느려진다.
핵심 메커니즘: 속도 누적
Momentum은 이전 단계의 업데이트 벡터(Velocity)를 기억하고, 그 중 일부(γ)를 현재 업데이트에 더한다.
- 진동하는 방향(부호가 계속 바뀌는 방향)의 기울기는 상쇄되어 줄어들고
- 일관된 방향(목표 지점 향함)의 기울기는 누적되어 가속도가 붙는다.
결과적으로 진동을 억제하면서 목표 지점으로 더 빠르고 안정적으로 수렴하게 된다.
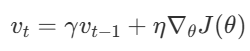
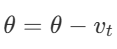
한계 및 발전
모멘텀은 관성으로 인해 멈춰야 할 지점을 지나칠(Overshooting) 수 있다는 단점이 있다. 이를 해결하기 위해 멈출 시점을 미리 예측하는 Nesterov Accelerated Gradient (NAG)가 제안되었으며, 이후 Adam 알고리즘의 1차 모멘트 추정 방식에 영감을 주었다.
2️⃣RMSProp
적응형 학습률 (Adaptive Learning Rate)
RMSProp은 모델의 파라미터마다 학습률을 다르게 적용하는 적응형 학습률 방법의 일종으로, AdaGrad의 단점을 보완하기 위해 고안되었다.
해결하고자 한 문제: 학습률 소실 (Vanishing Learning Rate)
AdaGrad는 각 파라미터의 과거 모든 기울기 제곱을 누적하여 학습률을 나눠준다. 이 방식은 희소한 데이터에는 유리하지만, 학습이 진행될수록 분모가 무한히 커져 학습률이 0에 수렴(Shrinking to zero)하여 학습이 중단되는 문제가 발생한다.
핵심 메커니즘: 지수 이동 평균(Exponential Moving Average)
RMSProp은 과거의 모든 기울기를 균등하게 누적하는 대신, 지수 이동 평균을 사용한다.
- 오래된 기울기의 영향력은 지수적으로 감소시키고, 최근의 기울기 정보를 더 크게 반영한다.
- 이를 통해 학습률이 급격히 줄어드는 것을 방지하면서도, 각 파라미터 상황에 맞춰 적절한 보폭으로 학습을 지속할 수 있다.


한계 및 발전
RMSProp은 Adam과 달리 초기화 편향 보정(Bias Correction) 단계가 없다. 이로 인해 학습 초기나 그래디언트가 희소할 때, 0으로 초기화된 이동 평균 값이 학습을 불안정하게 만들 수 있다. Adam은 RMSProp에 모멘텀을 더하고 편향 보정을 추가한 알고리즘이다.
3️⃣Adam
1. 서론
대규모 데이터와 파라미터를 다루는 딥러닝 모델 학습에 있어 확률적 최적화는 핵심적인 과제다. 목적 함수가 확률적(Stochastic)이거나 비정상(Non-stationary)인 경우, 효율적으로 전역 최솟값에 수렴하는 알고리즘이 필요하다.
본 논문에서 제안하는 Adam(Adaptive Moment Estimation)은 각 파라미터에 대한 학습률을 적응적으로 조절하기 위해 기울기의 1차 모멘트와 2차 모멘트를 추정하여 사용한다. 이 연구는 계산 효율성이 높고 메모리 요구량이 적으며, 기울기의 재조정(Rescaling)에 불변하는 1차 기울기 기반의 최적화 알고리즘을 제안한다.
2. 알고리즘 및 방법론
2.1 핵심 아이디어
Adam은 기존의 두 가지 성공적인 방법론의 장점을 결합하여 설계되었다.
- AdaGrad: 희소한(Sparse) 기울기를 다루는 데 강점이 있어 자연어 처리나 컴퓨터 비전 문제에 유리하다.
- RMSProp: 비정상(Non-stationary) 목적 함수에 유리하여 온라인 학습 등에 적합하다.
Adam은 이 두 가지 장점을 모두 취하면서도, 파라미터 공간의 차원이 높거나 데이터가 방대한 문제에서 효과적으로 동작하도록 설계되었다.
2.2. 모멘트 추정 (Moment Estimation)
알고리즘은 매 스텝(t)마다 목적 함수의 기울기(g_t)를 계산한 후, 기울기의 지수 이동 평균(Exponential Moving Average)을 통해 1차 및 2차 모멘트를 추정한다.
- 1차 모멘트 (m_t): 기울기의 평균을 추정한다. (Momentum과 유사)
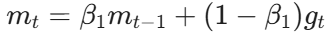
- 2차 모멘트 (v_t): 기울기 제곱의 평균(Uncentered Variance)을 추정한다. (RMSProp과 유사)

여기서 β _1과 β _2는 각 모멘트의 감쇠율(Decay Rate)을 결정하는 하이퍼파라미터로, 일반적으로 1에 가까운 값(예: 0.9, 0.999)으로 설정한다.
2.3. 편향 보정 (Bias Correction)
논문에서 가장 강조하는 RMSProp과의 주요 차별점은 편향 보정이다. m_t와 v_t는 0으로 초기화된 벡터에서 시작하기 때문에, 학습 초기 단계나 감쇠율이 1에 매우 가까울 경우 이 추정값들이 0으로 편향되는 경향이 있다.
이러한 초기 편향을 제거하고 참값에 근사하기 위해, 논문은 다음과 같은 보정식을 적용한다.
- 보정된 1차 모멘트:

- 보정된 2차 모멘트:
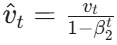
이 과정을 통해 학습 초기 단계에서도 적절한 크기의 스텝 사이즈를 확보할 수 있으며, 학습이 진행됨에 따라 보정 항(1- β^t)은 1에 수렴하여 영향력이 줄어든다. ( 이면 이므로 분모→1)
2.4. 업데이트 규칙
최종적으로 보정된 모멘트를 사용하여 파라미터를 업데이트한다.

- α : 스텝 사이즈(Learning Rate)
- : 0으로 나누는 것을 방지하기 위한 작은 상수
비율은 신호 대 잡음비(SNR)와 유사하게 동작하며, 이에 따라 스텝 사이즈가 자동으로 조절되는 효과를 가진다.
3. 주요 특징
Adam 알고리즘의 중요한 특징은 다음과 같다.
- 파라미터 업데이트의 크기 제한
업데이트 크기()는 스텝 사이즈 하이퍼파라미터 α에 의해 상한이 결정된다. 이는 신뢰 구간(Trust Region) 내에서 파라미터가 업데이트됨을 의미하며, 학습의 안정성을 보장한다.
- 기울기 스케일 불변성 (Scale Invariance)
기울기에 상수 c를 곱해도(c ⋅ g_t) 업데이트 식의 분자와 분모가 동시에 스케일링되어 상쇄되므로, 알고리즘의 동작은 변하지 않는다. - 하이퍼파라미터의 견고성
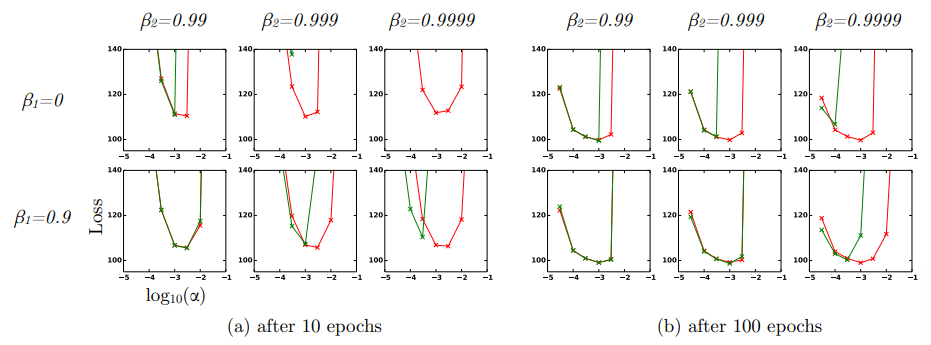
α, β _1, β_2 등은 직관적인 해석이 가능하며, 대부분의 문제에서 기본값(Default Settings)만으로도 우수한 성능을 보인다.- , , ,
- , , ,
실험 및 결과 (Experiments & Results)
본 연구에서는 볼록(Convex) 문제부터 비볼록(Non-convex) 문제까지 다양한 머신러닝 과제에서 Adam의 성능을 검증했다.
4.1. 실험 환경
- Logistic Regression: MNIST 이미지 분류 및 IMDB 영화 리뷰 데이터셋을 이용한 희소 데이터 분류
- Multi-layer Neural Networks (MLP): MNIST 데이터셋 (Dropout 적용)
- Convolutional Neural Networks (CNN): CIFAR-10 데이터셋
- Variational Auto-Encoders (VAE): 생성 모델 학습 및 편향 보정 효과 검증
4.2. 성능 비교
Adam과 SGD, AdaGrad, RMSProp, AdaDelta 등과 비교되었다.
- 수렴 속도
대부분의 실험, 특히 CNN과 MLP에서 Adam은 가장 빠른 수렴 속도를 보였다.
- CNN 실험에서 AdaGrad는 학습 초반에는 빠르지만, 2차 모멘트 추정값이 0으로 사라지며 학습이 정체되어 후반부에 수렴이 급격히 느려지는 현상이 관찰된다. 반면 Adam은 지속적으로 성능을 향상시켰다.
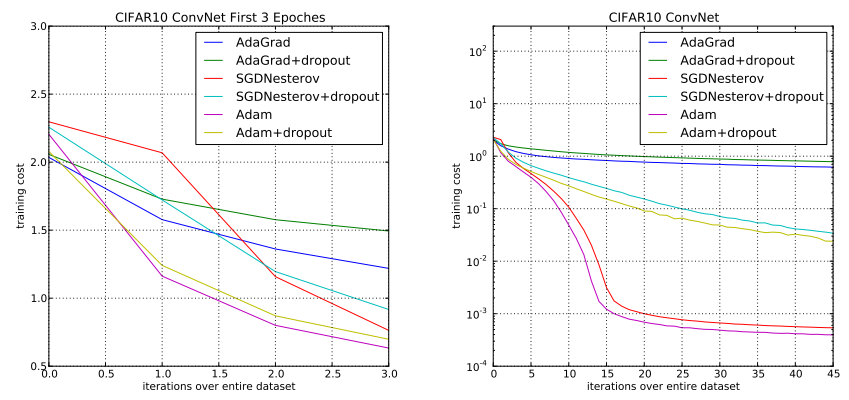
- 학습의 안정성 및 편향 보정
VAE 실험 결과, 편향 보정이 없는 경우(녹색선, RMSProp과 유사한 설정) 학습 초기에 발산하거나 불안정해지는 현상이 나타났다. Adam은 이 보정 단계를 통해 초기 학습부터 안정적으로 비용 함수를 감소시켰다.
- 희소 데이터 처리
IMDB 데이터셋을 이용한 로지스틱 회귀 실험에서, Adam은 희소한 피처를 다루는 데 강점이 있는 AdaGrad와 동등하거나 더 빠른 수렴 속도를 보였다. - 드롭아웃(Dropout)과의 호환성
드롭아웃을 적용한 MLP 실험에서 Adam은 다른 알고리즘 대비 최적화 효율성을 유지하며 빠르게 수렴했다.
5. 결론 (Conclusion)
Adam은 Adaptive Moment Estimation을 통해 각 파라미터별로 학습률을 효과적으로 조절하는 최적화 방법론이다. Adam은 단순히 RMSProp에 모멘텀을 더한 것이 아니라, 초기화 편향을 수학적으로 보정함으로써 학습 초기 불안정성을 해결했다는 점에서 중요한 기여를 했다.
결론적으로 Adam은 다음과 같은 이유로 현대 딥러닝의 기본(Default) 옵티마이저로 자리 잡았다.
- 구현이 간단하고 계산 효율적이다.
- 메모리 요구량이 적다.
- 하이퍼파라미터 튜닝에 민감하지 않고 초기 설정값으로도 잘 동작한다.
본 논문은 Adam이 대규모 데이터와 복잡한 신경망 구조를 다루는 현대 머신러닝 문제에 있어 강력하고 적합한 솔루션임을 이론과 실험을 통해 입증한다.
4️⃣AdamW
개념
AdamW는 널리 쓰이는 Adam 옵티마이저의 변형으로, Adam 알고리즘 내부에서 가중치 감쇠(Weight Decay)를 적용하는 방식을 수정하였다. 많은 딥러닝 프레임워크에서 Adam 사용 시 일반화 성능이 떨어지는 문제를 근본적으로 해결했다.
해결하고자 한 문제: L2 정규화와 가중치 감쇠의 불일치
표준 SGD에서는 L2 정규화와 가중치 감쇠가 수학적으로 동일하게 동작한다. 그러나 Adam과 같은 적응형 기울기(Adaptive Gradient) 알고리즘에서는 두 방식이 동일하지 않다.
- L2 정규화 (기존 Adam)
- 가중치 감쇠 (AdamW)
- Adam에 L2 정규화를 적용하면 정규화 항도 적응형 학습률 계수(1/√v_t)로 스케일링되어,
기울기가 큰 가중치의 정규화(감쇠 효과)가 약화/왜곡되는 현상이 발생한다. - 이로 인해 Adam은 SGD(Momentum)에 비해 일반화 성능이 떨어지는 결과가 나타났다.
핵심 메커니즘: 단계 분리 (Decoupling)
AdamW는 가중치 감쇠와 기울기 기반의 학습률 업데이트를 분리하여 서로 독립적으로 작용하므로 튜닝이 용이하다.
- 기존 Adam: L2 항이 기울기 g_t에 포함되어 1 / √ v_t로 스케일링됨
- AdamW
- 파라미터 업데이트 식에서 Adam의 최적화 스텝을 먼저 수행
- 학습률(α)과 가중치 감쇠 계수(λ)를 곱한 값을 파라미터에서 뺌
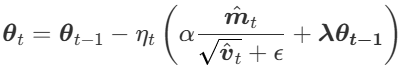
AdamW는 기울기가 큰 파라미터가 덜 정규화되는 Adam의 구조적 문제를 해결하고, Adam의 빠른 학습 속도와 SGD의 우수한 일반화 능력을 동시에 달성하였다.

