논문 제목: "ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION"
논문 정보: ICLR 2015에서 발표된 논문
논문 링크: https://arxiv.org/pdf/1412.6980
0. 초록
저자는 lower-order momentum의 adaptive estimates(적응적 추정치)를 기반으로 하는 확률론적 목표 함수의 1차 gradient 기반 최적화 알고리즘인 ADAM을 소개
다시 말해
Adam은 1차 moment인 평균과 2차 moment인 비중심화된 분산(uncentered variance)을 활용하고, 이에 대한 적응적 추정치를 활용하여 stepsize를 파라미터 별로 조정한다
이 방법은 실행하기 편하고 계산적으로 효율적이며, 적은 메모리 양으로 요구하는 동시에 gradient의 diagonal rescaling에 불변하고 마지막으로 데이터나 파라미터 측면에서의 거대한 문제들에 잘 맞음
또한 non-stationary objectives나 매우 noisy하고 sparse gradients를 가지는 문제에 적절함
하이퍼파라미터는 직관적으로 해석이 가능하며 거의 튜닝이 필요하지 않음
마지막으로 infinity norm을 기반으로 하는 ADAM의 변형 버전인 ADAMAX에 대해 논의함
1. 소개
확률론적 역전파(SGD) 기반 최적화는 많은 과학과 엔지니어링 분야에서 핵심이고 실용적으로 중요
이 분야에서 많은 문제들은 파라미터와 관련된 최대화 혹은 최소화를 요구하는 scalar parameterized 목표 함수의 최적화로 귀결됨
scalar parameterized 목표 함수란?
output이 1차원(scalar)이고 model parameter에 의해 값이 바뀌는 목표함수
만약 함수가 파라미터에 대해 미분가능하다면, 역전파는 상대적으로 효율적인 최적화 방법
왜냐하면 모든 파라미터에 대한 1차 미분 계산은 평가 함수의 계산 복잡도와 동일하기 때문
파라미터 수가 수백만 개여도 gradient 계산 시간이 forward 계산 시간보다 거의 늘어나지 않음
목표함수는 일반적으로 stochastic한데 예를 들어 많은 목표 함수들은 데이터의 다른 subsamples(또는 minibatch)에 대해 평가된 subfunctions의 합으로 구성됨
이 경우에 최적화는 개별적 subfunctions에 대한 gradient step을 취함으로써 더 효율적으로 만들어질 수 있음 (=stochastic gradient descent or ascent)
또한 목표 함수는 데이터 subsampling 외에도 dropout 같은 다른 noise를 가질 수 있음
목표 함수를 확률적으로 흔들리게 만드는 요소
= loss 값과 gradient가 매번 조금씩 달라지는 원인들
= Dropout, Mini batch
이러한 noisy한 목표 함수들에 대해 효율적인 확률론적 최적화 기술들이 필요
따라서 논문은 고차원 파라미터 공간을 가지는 확률론적 목표 함수의 최적화를 다룸
이 경우 고차 최적화 기법은 적합하지 않으며, 그러므로 본 논문에서는 1차 방법에 대해서만 논의할 것임
왜냐하면 2차 미분 정보만 사용해도 파라미터 수의 제곱만큼 계산 복잡도가 올라가기 때문임
ADAM은 gradients의 첫번째와 두번째 모멘트 추정을 활용하여 각 파라미터에 대한 개별적 적응형 학습률을 계산함
즉 ADAptive Moment estimation이라서 ADAM임
이 방법론은 sparse gradient에서 잘작동하는 AdaGrad와 on-line과 non-stationary 세팅에서 잘 작동하는 RMSProp을 혼합하여 고안됨
정리하면 ADAM의 장점은 1) 파라미터 업데이트의 크기가 gradient의 rescaling과 무관하며 2) stepsize는 hyperparameter에 의해 거의 bounded되어 있고 3) stationary objective를 필요로 하지 않으며 4) sparse gradients에서도 잘 작동하며 5) step size annealing(step size 감퇴)의 형태에서 자연스럽게 수행됨
2. 알고리즘

알고리즘 코드를 봐보자
$f(\theta)$가 noisy objective function이라고 일 때 (즉 파라미터에 대한 미분가능한 stochastic scalar function)
우리는 $\mathbb{E}[f(\theta)]$를 최소화하는 것에 관심이 있음
이때 확률성(stochasticity)는 랜덤한 subsamples(=minibatches)에 대한 평가 또는 일관적인 함수의 노이즈로부터 발생
$g_t=\nabla_\theta f_t(\theta)$를 t 시점에 대한 gradient라고 하자
알고리즘은 그래디언트의 지수이동 평균$m_t$와 지수 이동 평균의 제곱 그래디언트 $v_t$를 업데이트하는데 이때 하이퍼 파라미터 $\beta_1,\beta_2\in[0,1)$은 이러한 이동 평균의 지수적 decay rate를 통제함
이동 평균들은 각각 1차 모먼트(평균)와 2차 raw 모먼트(중심 이탈 분산 - 평균을 빼지 않은 분산)임
하지만 이 이동 평균들은 0으로 초기화되고 이는 0으로 편향된 모먼트 추정치라는 결과를 낳게 됨
이 편향은 특히나 초기 단계에 심하며 decay rates가 작을 때($\beta$들이 1에 가까울 때) 심함
다행히도 이러한 초기 편향은 편향 조정된 추정치 $\hat m_t$와 $\hat v_t$로 쉽게 대처할 수 있음
2.1 ADAM’s Update Rule
Adam의 업데이터 rule의 중요한 특성은 바로 신중한 stepsize의 선택에 있음
Adam은 고정된 lr을 쓰지 않으며 parameter마다 adaptive하게 step size를 조절함
(분석을 위해) $\epsilon=0$이라고 가정할 때 타임스텝 $t$시점 파라미터 공간 내에서 취해진 효과적인 step은 $\Delta_t=\alpha\cdot\hat m_t/\sqrt{\hat v_t}$임
효과적인 stepsize는 두 개의 upper bounds(상한)를 가짐: 1)$(1-\beta_1)>\sqrt{1-\beta_2}$로 선택한 경우,
$|\Delta_t|\le\alpha\cdot(1-\beta_1)/\sqrt{1-\beta_2}$ 2) 반대의 경우, $|\Delta_t|\le\alpha$
첫 번째 케이스가 상한에 도달하는 것은 sparsity가 극심한 경우에만 발생함 (gradient가 현재 timestep을 제외한 모든 step에서 0일 경우)
less sparse한 경우에는 effective stepsize가 작음 ($\sqrt{v_t}$가 커지기 때문)
즉 Gradient 패턴에 따라 stepsize 조절됨
$(1-\beta_1)=\sqrt{1-\beta_2}$일 때는 $|\hat m_t/\sqrt{\hat v_t}|<1$이므로 $|\Delta_t|<\alpha$임
(참고: 부등호는 Cauchy-Schwarz에 의해 성립됨 ⇒ $||a||^2\cdot||b||^2\ge|a\cdot b|^2$)
일반적인 상황에서 $[\mathbb{E}[g]/\sqrt{\mathbb{E}[g^2]}]\le1$이기 때문에 $\hat m_t/\sqrt{\hat v_t}\approx \pm 1$를 가지게 될 것임
그러므로 steps의 효과적인 크기는 stepsize setting $\alpha$에 의해 대략적으로 bounded됨 ($|\Delta_t|\lessapprox\alpha$)
이는 현재 파라미터 값 주변에 trust region(현 위치에서 gradient 정보가 신뢰할 수 있는 범위)을 설정하는 것과 같은 효과이며 이 영역을 벗어나면 현재 gradient 추정치가 충분한 정보를 제공하지 못함 (Parameter Space에서 한 번에 이동할 수 있는 최대 거리가 $\alpha$가 되는 셈)
이는 일반적으로 $\alpha$의 적절한 scale을 미리 아는 것을 비교적으로 쉽게 만듦
예를 들어, 많은 머신러닝 모델에서 우리는 종종 좋은 최적해가 높은 확률로 parameter space의 어떤 정해진 영역 내에 있다는 것을 미리 알고 있음 (예를 들어, parameter에 대한 prior distribution을 갖는 것이 드문 일이 아님)
예를 들어 우리는 layer를 어떠한 initialization 방법으로 초기화하는데 이때 우리는 그 분포 근처에 최적의 해가 있다는 것을 알고 있는 것임 (따라서 $\alpha$를 (parameter의 범위) / (iteration 수)로 설정하면 되는 것임)
$\alpha$가 파라미터 공간에서 step의 크기(상한)를 설정하기 때문에 $\theta_0$에서 어떤 iteration 수 내에 최적해에 도달할 수 있도록 $\alpha$의 올바른 order of magnitude를 추정할 수 있음
이어서 비율 $\hat m_t/\sqrt{\hat v_t}$를 Signal-to-Noise Ratio (SNR)이라고 하자
$\hat m_t$: 신호 → $\mathbb{E}[g]$→일관된 gradient의 방향
$\sqrt{\hat v_t}$: 노이즈 → $\mathbb{E}[g^2]$ → gradient의 변동성
SNR이 작을 수록 효과적인 step size $\Delta_t$는 0에 가까워 질 것임
낮은 SNR = 불확실성이 높다 → 조금만 움직인다
이는 바람직한 특성인데 왜냐하면 더 작은 SNR은 $\hat m_t$의 방향이 진짜 gradient의 방향과 일치하는 지에 대한 더 큰 불확실성이 있다는 것을 의미하기 때문임
예를 들어 SNR 값은 일반적으로 최적해에 가까워질수록 0에 가까워지며, parameter space에서 더 작은 효과적인 step으로 이어지며 이는 일종의 자동 annealing임
ADAM의 또다른 특징은 효과적인 stepsize $\Delta_t$는 gradient의 scale에 대해서 불변한다는 점임
gradient g를 인수 c로 rescaling하면 $\hat m_t$는 인수 $c$로 $\hat v_t$는 인수 $c^2$로 scale되며 이들은 상쇄됨: $(c\cdot\hat m_t)/(\sqrt{c^2\cdot\hat v_t})=\hat m_t/\sqrt{\hat v_t}$
3. Initialization Bias Correction
여기서는 second moment 추정치에 대한 항만 유도할 것이며 first moment 추정치에 대한 유도는 완전히 유사하기 때문에 생략
$g$를 stocahstic objective $f$의 gradient라고 하고, decay rate $\beta_2$를 가진 제곱 gradient의 exponential moving average를 사용하여 그것의 second raw moment (uncentered variance)를 추정하고자 함
$g_1,...,g_t$를 연속된 timestep에서의 gradient라고 하고, 각각은 기본 gradient 분포 $g_t \sim p(g_t)$로부터의 샘플임 (예를 들어 t개의 minibatch라고 생각해도 됨)
이때 exponential moving average를 $v_0=0$ (영벡터)로 초기화
먼저 timestep t에서의 exponential moving average의 업데이트 $v_t=\beta_2\cdot v_{t-1}+(1-\beta_2)\cdot g^2_t$가 모든 이전 timestep의 gradient들의 함수로 쓰여질 수 있다는 것을 주목하자
즉 $v_t=(1-\beta_2)\Sigma_{i=1}^t\beta_2^{t-i}\cdot g^2_i$
이때 저자는 timestep t에서 exponential moving average의 기댓값 $\mathbb{E}[v_t]$가 진짜 second moment $\mathbb{E}[g_t^2]$와 어떻게 관련되는 지 알고 싶으며, 그래서 둘 사이의 불일치를 보정하고 싶음
바로 위 수식에 좌변과 우변에 기댓값을 취하면
$\mathbb{E}[v_t]=\mathbb{E}[(1-\beta_2)\Sigma_{i=1}^t\beta_2^{t-i}\cdot g^2_i]$
정리하면
$=\mathbb{E}[g_t^2]\cdot(1-\beta_2)\Sigma_{i=1}^t\beta_2^{t-i}+\zeta=\mathbb{E}[g_t^2]\cdot(1-\beta_2^t)+\zeta$
stationary하다면 i에 무관하므로 $\mathbb{E}[g_1^2]=\mathbb{E}[g_2^2]=...=\mathbb{E}[g_t^2]$임
$\Sigma_{i=1}^t \beta_2^{t-1}=\beta_2^{t-1}+\beta_2^{t-2}+...+\beta_2+1=(1-\beta_2^t)/(1-\beta_2)$
이때 true second moment $\mathbb{E}[g_i^2]$이 stationary하다면 $\zeta=0$이고 그렇지 않다면 exponential moving average가 너무 과거의 gradient에 작은 가중치를 할당하도록 exponential decay rate $\beta_2$을 선택할 수 (그리고 해야) 있기 때문에 $\zeta$를 작게 유지할 수 있음 (beta를 통해 오래된 gradient의 가중치가 줄어들면서 영향이 감소하기 때문에 $\zeta$가 작게 유지됨)
그러면 남는 것은 running average를 0으로 초기화함으로써 발생하는 항 $(1-\beta_2^t)$임
따라서 알고리즘 1에서 저자는 initialization bias를 보정하기 위해 이 항으로 나눔
Sparse gradient의 경우, second moment의 신뢰할 수 있는 추정을 위해서는 작은 $\beta_2$ 값을 선택하여 많은 gradient에 결쳐 평균을 내야 함; 그러나 intialization bias correction이 없다면 훨씬 더 큰 초기 step으로 이어지는 것은 정확히 이 작은 $\beta_2$의 경우임
sparse feature는 가끔만 나타나므로, 나타났을 때의 최근 정보가 중요하기 때문에 작은 $\beta_2$로 오래된 정보를 빨리 잊어야 함
그런데 $\beta_2$가 작으면 $(1-\beta_2^t)$가 빠르게 1에 근접
예를 들어,
$\beta_2=0.999$라면 $(1-\beta_2^{100})=0.095$→ 첫번째 정보가 아직 90% 남아있음
$\beta_2=0.9$라면 $(1-\beta_2^{100})=0.99997$→ 첫번째 정보가 거의 사라짐
즉 과거의 정보가 더 빨리 사라짐
다만 $\beta_2$가 낮을 수록 sparse한 상황 시 update가 매우 크게 이뤄져서 initialization bias correction이 필요함
4. Convergence Analysis
저자는 Zinkevich, 2003에서 제안된 online learning framework를 사용하여 Adam의 수렴성을 분석
Online Learning Framework란?
- 각 데이터가 순차적으로 도착 → 각 step마다 예측하고 loss 관찰 → Regret을 최소화하도록 목표
- Offline 학습: 전체 데이터 셋 미리 알고 최적화
- Online 학습: 데이터를 하나씩 보면서 학습
임의의, 미지의 convex cost function 시퀀스 $f_1(\theta),f_2(\theta),...,f_t(\theta)$가 주어졌다고 하자
각 시간 t에서 저자의 목표는 파라미터 $\theta_t$를 예측하고 이전에 알려지지 않은 cost function $f_t$에 대해 평가하는 것임
Online Learning: Learner(저자)가 $\theta_t$ 선택 → Adversary(환경)에서 $f_t$ 공개 → Learner가 loss $f_t(\theta_t)$를 받음
(순서가 중요함) $\theta_t$를 선택할 때는 $f_t$를 모르지만 과거 $f_1,...,f_{t-1}$만 알고 있음
시퀀스의 성질을 미리 알 수 없으므로, 저자는 regret을 사용하여 알고리즘을 평가함
regret은 online 예측 $f_t(\theta_t)$와 모든 이전 step에 대해 feasible set X로부터의 최고의 고정된 점 parameter $f_t(\theta^*)$의 차이를 모두 합한 것임 (이때 X는 파라미터 제약 영역임)
Regret: “만약 최고의 고정 parameter를 미리 알았다면 얼마나 더 잘할 수 있었을까?”
$R(T)=\Sigma_{i=1}^T[f_t(\theta_t)-f_t(\theta^*)]$
이때 $\theta^*=\arg\min_{\theta\in \chi}\Sigma_{t=1}^Tf_t(\theta)$ (모든 T개의 함수에 대한 총 loss를 최소화하는 parameter)
저자는 Adam이 $O(\sqrt T)$ regret bound를 가진다는 것을 보이며 증명은 appendix에서 제공
즉 $R(T)\le O(\sqrt T)$ → T step 후 regret은 최대 $\sqrt T$에 비례
평균 Regret은 $R(T)/T \le O(\frac 1 {\sqrt T})$→ 0에 근사
저자의 결과가 convex online learning 문제에 대해서 SOTA의 bound와 비교할만함
(SGD와 Adagrad 모두 $O(\sqrt T)$, RMSProp은 이론적 보장X)
저자는 또한 표기를 단순화하기 위해 몇 가지 정의를 사용했는데 $g_t\triangleq\nabla f_t(\theta_t)$이고 $g_{t,i}$는 i번째 element를 의미함 ($\triangleq$: ~라고 정의한다)
저자는 $g_{1:t,i}\in \mathbb{R}^t$를 t까지 모든 iteration에 걸쳐 gradient의 i번째 dimension을 포함하는 벡터로 정의
즉 $g_{1:t,i}=[g_{1,i},g_{2,i},...,g_{t,i}]$
또한 $\gamma\triangleq \frac{\beta_1^2}{\sqrt{\beta_2}}$라고 정의함
다음 정리는 learning rate $\alpha_t$가 $t^{-1/2}$의 비율로 감소하고 first moment running average coefficient $\beta_{1,t}$가 $\gamma$로 exponentially decay할 때 성립하며, $\gamma$는 일반적으로 1에 가까움
(예를 들어 $1-10^{-8}$)
정리 4.1
함수 $f_t$가 bounded gradient를 가진다고 가정하자 모든 $\theta\in\mathbb{R}^d$에 대해 $||\nabla f_t(\theta)||_2\le G, \ ||\nabla f_t(\theta)||_{\infty}\le G_{\infty}$이고 Adam이 생성한 임의의 $\theta_t$ 사이의 거리가 bounded되어 있다고 가정하자.
임의의 $m,n\in{1,..,T}$에 대해 $||\theta_n-\theta_m||_2\le D, \ ||\theta_m-\theta_n||_{\infty}\le D_{\infty}$이며, $\beta_1,\beta_2\in[0,1)$는 $\beta_2^2/\sqrt{1-\beta_2}<1$을 만족한다고 하자
그리고 $\alpha_t=\alpha/\sqrt{t}$이고 $\beta_{1,t}=\beta_1\lambda^{t-1},\lambda\in(0,1)$라고 하자
이때 Adam은 모든 $T\ge1$에 대해 다음을 보장함
$R(T)\le \frac{D^2}{2\alpha(1-\beta_1)}\Sigma^d_{i=1}\sqrt{T\hat v_{T,i}}+\frac{\alpha(1+\beta_1)G_{\infty}}{(1-\beta_1)\sqrt{1-\beta_2}(1-\gamma)^2}\Sigma_{i=1}^d||g_{1:T,i}||2+\Sigma_{i=1}^d \frac{D^2_{\infty}\sqrt{1-\beta_2}}{2\alpha(1-\beta_1)(1-\lambda)^2}$
첫번째 항(거리 관련 항) $\frac{D^2}{2\alpha(1-\beta_1)}\Sigma^d_{i=1}\sqrt{T\hat v_{T,i}}$
⇒ Parameter 거리 D에 비례, Learning rate $\alpha$에 반비례, Second moment에 의존
두번째 항(학습률 관련 항) $\frac{\alpha(1+\beta_1)G_{\infty}}{(1-\beta_1)\sqrt{1-\beta_2}(1-\gamma)^2}\Sigma_{i=1}^d||g_{1:T,i}||_2$
⇒ Gradient 크기에 비례, Learning rate $\alpha$에 비례, Dimension 별 gradient 합
세 번째 항(모멘텀 감쇠 관련 항) $\Sigma_{i=1}^d \frac{D^2_{\infty}\sqrt{1-\beta_2}}{2\alpha(1-\beta_1)(1-\lambda)^2}$
⇒Moentum decay $\lambda$에 의존, 상수항
이 정리는 데이터 feature가 sparse하고 gradient가 bounded일 때, summation 항이 그 upperbound $\Sigma_{i=1}^d||g_{1:t,i}||_2 \ll dG_{\infty}\sqrt{T}$ 및 $\Sigma_{i=1}^d\sqrt{T\hat v_{t,i}}\ll dG_{\infty}\sqrt{T}$보다 훨씬 작을 수 있음을 의미하며, 특히 function과 data feature의 class가 Duchi et al의 section 1.2 형태인 경우에 그러함
Worst case(dense): $\Sigma_{i=1}^d||g_{1:t,i}||_2 \ll dG_{\infty}\sqrt{T}=O(d\sqrt T)$
왜 이렇게 나오는가?
$|g_{t,i}| \le G_{\infty}$이라는 가정을 했으므로
$\hat v_{T,i} \le G_{\infty}^2 \to \sqrt{T\hat v_{T,i}}\le G_{\infty}\sqrt T$
또한 $||g_{1:T,i}||_2=\sqrt{\Sigma_{t=1}^Tg_{t,i}^2} \le G_{\infty}\sqrt T$
이를 $R(T)$에 대입하면 $R(T) = O(d\sqrt T)$가 된다
Worst case(Sparse): k(k << d) 개만 non-zero라고 하면 $\Sigma_{i=1}^d||g_{1:t,i}||_2 \approx d\sqrt{kT/d}\cdot G_{\infty}=d\sqrt{kdT}\cdot G_{\infty}=O(\sqrt{kdT})$
왜 이렇게 나오는가?
$\Sigma_{i=1}^d ||g_{1:T,i}||_2=\Sigma_{i=1}^d\sqrt{\Sigma_{t=1}^Tg_{t,i}^2}$
위 수식에서 Cauchy-Shcwarz에 의해
(참고: $\Sigma_{i=1}^d a_i \le \sqrt d \sqrt{\Sigma_{i=1}^da_i^2}$)
$\Sigma_{i=1}^d ||g_{1:T,i}||_2 \le \sqrt d \sqrt{\Sigma_{i=1}^d\Sigma_{t=1}^Tg_{t,i}^2}$
여기서 시그마의 순서를 바꾸면
$\Sigma_{i=1}^d\Sigma_{t=1}^Tg_{t,i}^2 = \Sigma_{t=1}^T||g_t||_2^2$
이때 $||g_t||_2^2\le kG^2$이므로
$\Sigma_{t=1}^T ||g_t||_2^2 \le kT$ ($G^2$생략)
최종적으로는 $\Sigma_{i=1}^d ||g_{1:T,i}||_2 \le \sqrt d \sqrt{kT} = \sqrt{kdT}$
$\Sigma_{i=1}^d||g_{1:t,i}||_2$의 기댓값에 대한 그들(Adagrad논문)의 결과도 Adam에 적용됨
(Adagrad 논문 결과 $\mathbb{E}[\Sigma_{i=1}^d||g_{1:t,i}||_2]=O(\sqrt{kdT})$)
이번에는 gradient가 아닌 d차원 입력 feature 측면에서 보면 Adam과 Adagrad 같은 adaptive method는 $O(\log d\sqrt T)$를 달성할 수 있으며 이는 non-adaptive method의 $O(\sqrt {dT})$보다 개선된 것임
또한, $\beta_{1,t}$를 0으로 decay시키는 것은 저자의 이론적 분석에서 중요하며 이전의 경험적 발견과도 일치함
예를 들어 Sutskever et al. 2013은 학습 마지막에 momentum coefficient를 줄이는 것이 수렴을 개선할 수 있다고 제안함
이론 상으로는 $\beta_1$을 $\lambda^{t-1}$을 곱해줌으로써 decay가 필요하지만 실전에서는 $\beta_1$을 고정시켜도 잘됨
마지막으로 Adam의 평균 regret이 수렴함을 보일 수 있음
따름 정리 4.2
정리 4.1과 동일한 가정하에서
$R(T)/T=O(1\sqrt T)$
즉 $T \to \infty$이면 $R(T)/T \to 0$
충분히 오래 학습하면 최선의 고정 parameter만큼 잘함!
이 결과는 정리 4.1과 $\Sigma_{i=1}^d||g_{1:t,i}||_2 \ll dG_{\infty}\sqrt{T}$를 사용하여 얻을 수 있음.
따라서, $\lim_{T\to \infty}R(T)/T=0$임
6. Experiements

Figure 1(좌)에서는 Adam이 SGD+Momentum(SGDNesterov)와 비슷하게 수렴함을 보이고 Adagrad보다 빠르게 수렴함을 보임
과거 연구에 따르면 SGD와 달리 Adagrad가 sparse features와 gradients를 다루는데 효율적임
Adam은 Adagrad와 이론적으로 볼 때 성능이 비슷하게 나올 것임
이를 확인하기 위해 sparse feature prblem인 IMDB movie review dataset을 가지고 실험 진행
그래서 Figure 1(우)에서는 Adagrad가 노이즈(분산)도 적은 모습으로 큰 gap으로 SGD + Momentum을 이김
Adam도 Adagrad만큼 빠르게 수렴했음
Adam은 특히 multi-layer neural network에서 다른 방법론보다 outperform함을 보였음

뿐만 아니라 CNN 계열의 모델에서도 Adam의 효과성을 검증함

흥미로운 점은 Adam과 Adagrad는 학습 초기에 빠른 속도로 cost를 줄임(Figure 3-좌측)
전체 학습 과정으로 볼 때(Figure 3 - 우측) Adam과 SGD가 Adagrad보다 빠르게 수렴함
저자는 second moment estimate인 $\hat v_t$가 초기 에포크 이후에 0으로 사라지면서 $\epsilon$에 의해 dominated됨을 발견
따라서 second moment estimate는 multi-layer에 비해 CNN의 cost function의 geometry에는 poor approximation이었음
반면, first moment를 통해 minibatch 분산을 줄이는 것은 CNN 계열에서 매우 중요했고 speed-up에 기여함
정리하면 Adam의 추가적인 성능 향상은 SGD에서 직접 선택하는 것과 달리 learning rate scale이 adaptive하게 적용된다는 점에서 비롯됨
마지막으로 bias correction terms의 효과를 실험을 통해 평가
bias correction terms의 제거는 RMSProp + Momentum과 동일함
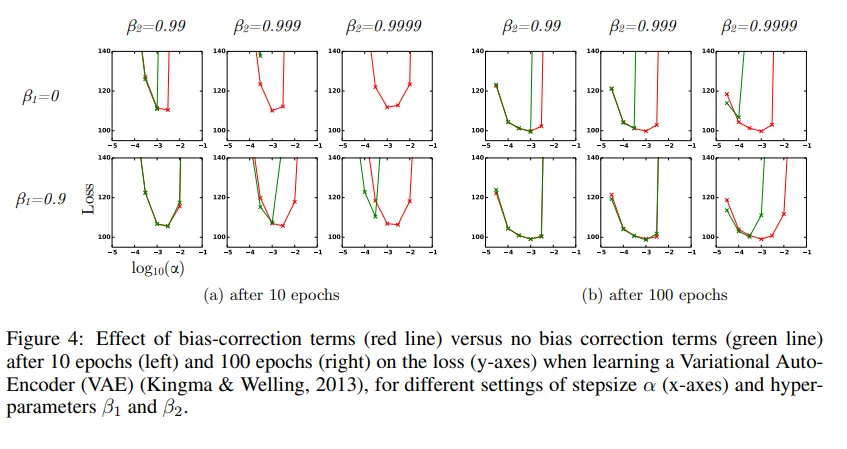
$\beta_2$가 1에 가까워질 수록 initialization bias가 커지고 bias correction term이 더욱 중요해지는 순간임
Figure 4에서 보면 $\beta_2$가 1에 가까워질 수록 학습에서의 불안정성을 유발함
7. ADAMAX
저자의 아이디어
$v_t$는 gradient의 L2 norm에 기반하는데 다른 L-p norm은 어떨까?
문제는 p가 커질 수록 수치적으로 불안정
놀라운 점은 p가 $\infty$로 가면 오히려 단순하고 안정적으로 된다는 점임
$v_t=\beta_2^p\cdot v_{t-1}+(1-\beta_2^p)\cdot |g_t|^p$
여기서 $\beta_2$가 아닌 $\beta_2^p$를 취하는 이유는 $v_t^{1/p}$ 연산의 편의성을 위해서임
핵심 유도
목표: $\lim_{p\to\infty}v_t^{\frac 1 p}$ 계산
$v_t=(1-\beta_2^p)\Sigma_{i=1}^t\beta_2^{p(t-i)}\cdot|g_i|^p$
$v_t=\lim_{p\to\infty}v_t^{\frac 1 p}=\lim_{p\to\infty}[(1-\beta_2^p)\Sigma_{i=1}^t\beta_2^{p(t-i)}\cdot|g_i|^p]^{1/p}$
- $\lim_{p\to\infty}(1-\beta_2^p)^{1/p}$ 이때 $\beta_2\in[0,1)$이므로 $\lim_{p\to\infty}(1-0)^{1/p}=1$
- $\lim_{p\to\infty}[\Sigma_{i=1}^t\beta_2^{p(t-i)}\cdot|g_i|^p]^{1/p}$
→ $\lim_{p\to\infty}[\Sigma_{i=1}^na_i^p]^{1/p}=\max_i a_i$
따라서 $v_t=\max_{1\le i\le t}\{\beta_2^{t-i}|g_i|\}=\max\{\beta_2^{t-1}|g_1|,\beta_2^{t-2}|g_2|,...,\beta_2|g_{t-1}|,|g_t|\}$
AdaMax 장점
- 큰 gradient가 와도 $v_t$는 선형적으로만 증가(max연산 기반이기 때문) 반면 Adam은 제곱이라 폭발 가능
- 메모리 효율(제곱 연산X,제곱근 연산X)

