논문 소개: “LIME의 불안정성을 보완. ‘조건문(anchor)’ 형태로 국소적 설명을 안정적으로 제공하는 논문”, 2018년 AAAI 학회에서 발표됨
인용 수: 2025.11.01 기준 3165회
논문 링크: https://ojs.aaai.org/index.php/aaai/article/view/11491
Anchors: High-Precision Model-Agnostic Explanations | Proceedings of the AAAI Conference on Artificial Intelligence
ojs.aaai.org
Anchors: 닻
→ 조건문 기반으로 모델을 안정적으로 설명하기 위해 붙잡아 두는 역할
Abstract
저자는 anchors라고 불리는 high-precision rules를 가지는 복잡한 모델의 행동을 설명하는 새로운 model-agnostic 시스템을 제안
anchors는 예측을 위한 local, “sufficient” 조건들을 의미함
저자는 어떠한 black-box 모델에서든 high-probability guarantee를 가지는 이러한 explanations를 효율적으로 계산하는 알고리즘을 제안함
다양한 도메인과 태스크에 대해 수많은 모델들을 설명함으로써 anchors의 유연성을 증명
user study에서는 기존 선형 explanations에 비해 anchors가 users들이 어떻게 모델이 unseen instances에서 행동하는 지를 적은 노력과 높은 precision으로 예측할 수 있게 해줌
Introduction
복잡한 머신러닝 모델들은 복잡한 구조로 인해 거의 블랙박스로 만듦에도 불구하고 많은 정확도를 보임
users들이 이러한 모델의 행동을 이해할 필요가 있음에 따라 해석가능한 머신 러닝이 최근 뜨고 있음
이는 globally-해석 가능 머신러닝부터 local explanations까지 연구되고 있음
해석 가능성에 대한 핵심 질문은 '인간이 unseen instances의 행동에 대한 정확한 예측을 하기에 충분히 모델에 대해 이해가 되는가?'임
높은 인간 정밀도(human precision)은 실제 해석 가능성에 매우 중요함
대부분의 local 접근법은 입력 feature들의 선형적으로 가중치된 조합을 사용하여 모델의 local 행동을 묘사
선형 함수는 쉽게 이해할 수 있는 방식으로 feature들의 상대적 중요성을 포착할 수 있음
하지만 이러한 선형 explanations가 지역적이라는 점으로 인해 이를 unseen instance에 적용하는 것은 불분명함
즉, 그들의 coverage(explanation이 적용 가능한 범위)가 불확실 함
불확실한 coverage는 user들이 explanation을 통한 인사이트가 unseen instances에 적용된다고 믿을 수 있기 때문에 낮은 인간 정밀도의 결과를 낳음

위 이미지의 LIME의 감정 분석 케이스를 예시로 들면, 두 explanations이 locally accurate하게 계산되었음에도 왼쪽에서의 설명(The movie is not bad)을 오른쪽(This movie is not very good)에 적용한다면 “not”이 긍정적인 영향을 미친다고 생각할 수 있음(사실은 그렇지 않음)
이는 모델의 coverage가 명확하지 않기 때문임(즉 언제 “not”이 감정 분석에 긍정적인 영향을 미칠까?)
따라서 저자는 anchors라고 하는 if-then rules를 기반으로 하는 새로운 model-agnostic explanations를 제안
anchor explanation은 예측을 로컬에서 단단히 붙잡아서 나머지 feature value들의 변화가 중요하지 않도록 하는 rule임 → 나머지 feature 값들이 바뀌어도 예측 결과에는 거의 영향이 없음. anchor 규칙에서 명시된 feature들만 중요 (Ex- “무료”가 들어가면 → Spam, 나머지 단어는 영향 X)
즉, anchor가 성립하는 instances들에 대해 prediction은 거의 항상 동일하다.
→ 예측을 anchoring(고정)한다.
위 이미지에서도 볼 수 있듯 “not”과 “bad”가 함께 나온다면 긍정의 뜻을 가진다~ 이렇게 rule을 만들 수 있음
Anchors는 직관적이며 이해하기 쉽고 매우 명확한 coverage를 가짐 - 오직 rule이 충족되었을 때만 적용되므로 precision이 높음
Anchors as High-Precision Explanations
주어진 블랙박스 모델 $f:X\to Y$와 instance $x \in X$에 대해 local model-agnostic 해석 가능성의 목표는 $f(x)$의 행동을 유저에게 설명하는 것임
이때 $f(x)$는 인스턴스 $x$에 대한 개별적인 예측을 의미
모델이 globally하게 너무 복잡해서 간결하게 설명하기 어려운 반면, 개별적인 예측으로의 “zooming in”은 explanation task를 실현 가능하게 만든다고 가정
대부분의 model-agnostic 방법은 “perturbation distribution” $\mathcal{D}_x$을 따라 instance $x$를 섭동함으로써 작동함
저자는 이 perturbations $\mathcal{D}$가 모델이 인풋으로 다른 표현을 사용해도 (인간에게) 해석가능한 표현이어야 한다고 강조함
A가 그런 해석가능한 표현에 대해 작동하는 rule(set of predicates)이라고 하면 $A(x)$는 모든 feature predicates가 instance $x$에 대해 모두 true일 경우 1을 반환함
예) $x='This\ \ movie\ \ is\ \ not\ \ bad',\ \ f(x) = Positive$, $A={'not','bad'}$, $A(x) = 1$

이때 A가 anchor가 되는 조건은 다음과 같음(여기서 저자는 tau를 0.95로 설정)
$\mathbb{E}_{\mathcal{D}(z|A)}[𝟙_{f(x)=f(z)}]\ge \tau,\ A(x)=1$
Figure 2b는 복잡한 모델의 두 “zoomed in” region를 보여줌
LIME explanations는 $\mathcal{D}$ 아래서 (local weighting과 함께) 모델에 가장 근사하는 선을 배움으로써 작동함
이 결과는 얼마나 그들이 충실한지 또는 그들의 “local region”이 어떤지 전혀 알지 못함
그에 반해 anchor는 같은 $\mathcal{D}$에서 충실하며 coverage를 명확히 알 수 있음(Figure 2b 네모 anchor)
각 태스크에 대한 예시
Text Classification: LSTM 모델을 사용할 경우 모델의 input은 해석가능하지 않음
대신 개별적인 토큰의 존재 여부(2진 벡터)로 사용
perturbation distribution $\mathcal{D}$는 특정 단어를 랜덤하게 교체하며 동시에 그 자리에 임베딩 공간에서의 유사도에 비례하는 확률로 같은 POS(품사) tag를 가지는 것으로 작동
Structured prediction: 만약 알고리즘의 출력이 structure이라면 anchor 접근은 출력의 어떤 함수도 설명하는데 사용할 수 있음
Anchors는 특히 구조화된 예측 모델에 적합: global 행동이 너무 복잡해서 단순 해석 모델에 의해 포착하기 어려운 반면 local 행동은 짧은 규칙을 사용해서 표현될 수 있는 경우

Table 1에서 SOTA part-of-speech tagger의 “play”에 대한 예측을 다양한 컨텍스트에서 설명
anchor는 모델이 영어 언어의 합리적인 패턴을 뽑음을 설명

Table 2에서는 multi-layer RNN encoder / attention-based decoder 번역 시스템에 대한 anchor를 계산(English-Portuguese 병렬 corpora에서 훈련됨)
이 경우 anchor는 번역 내 단어의 존재를 설명함
anchor(볼드체)는 포트투갈 핑크색 텍스트 단어의 존재와 상응하도록 계산됨
첫번째 행은 “This”,”is”,와 “question”이 영어로 나타나고 “Esta”라는 단어가 번역에 포함됨
포르투갈어에서 “this”는 단어의 성별에 의존(”esta”는 여성형, “este”는 남성형 단어)하거나 참고할 단어가 없을 때 “isso”라고 함
anchors는 모델이 “this is” 또는 “this”가 참조하는 단어인 “question”(여성형 단어) 또는 “problem”(남성형 단어)를 포착하는 모습을 보임
Tabular Classification: validation dataset으로 $\mathcal{D}$를 정의하고 A 내에서 predicates를 고정하고 나머지 행을 전체로서 샘플링함으로써 $\mathcal{D}(z|A)$로부터 샘플링
→ anchor에 들어가는 feature 기준으로 고정하고 나머지는 상관없으므로 그 전체 행들을 가져옴
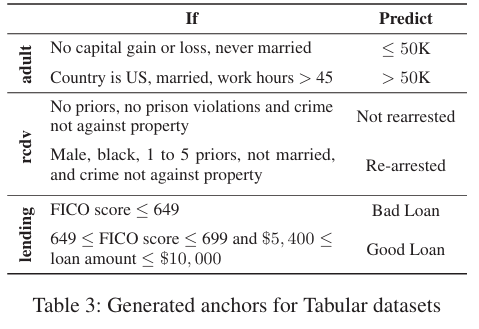
anchor는 adult 데이터 셋에서 “사람의 연소득이 5만 달러를 초과하는지를 예측할 때, 결혼 여부(Marital status)가 여러 anchor 설명들에 공통적으로 등장”한다고 설명
rcdv 데이터 셋에서는 "인종과 성별이 두드러지게 나타난다”라고 설명했는데 이는 모델을 사용할 경우 fiarness issue가 드러난다는 문제가 있음
→인종, 성별 편향이 있음을 anchor가 보여줌
lending 데이터 셋에서는 대출이 부실이 될지를 예측할 때 FICO 점수가 매우 높거나 매우 낮은 극단적인 경우에는 그 점수만으로 충분하지만, 그 외의 경우에는 대출 금액(loan amount)도 함께 고려해야 함을 설명
다만 모델은 복잡하기 때문에 anchor는 입력 공간의 일부에서의 행동을 설명할 뿐이지 모델 전체를 완전히 설명하는 것은 아님
특히나 경계 부근의 사례들에 대한 anchor는 더 길어질 수 있음(긴 anchor가 필요하기 때문임)
Image Classification: 주로 superpixel의 존재/부재를 가지고 해석가능한 표현을 만듦
저자는 superpixels를 숨기는 대신 원본 이미지에 A 내 superpixels를 고정하고 나머지 superpixels에 대해 다른 이미지를 중첩(대체)함으로써 $\mathcal{D}(z|A)$를 정의

$\mathcal{D}$가 여기서 꽤 비현실적이지만 anchor는 모델이 그 품종을 결정하기 위해 다양한 강아지의 부분에 집중함을 설명
Visual Question Answering (VQA): 마지막으로 VQA 태스크에서 저자는 질문의 어떤 부분이 예측된 대답으로 이어지는 지를 판단하고 싶어함
그러므로 Figure 2b와 동일한 표현과 분포를 사용하였고 Figure 3a의 이미지를 사용
figure 3d에서 짧은 앵커(“What”)는 이 이미지에 대해 모델이 여러 질문에 거의 항상 “dog”이라고 대답한다는 사실을 보여줌
→”What”만 들어가면 모두 “dog”라고 대답함(잘못된 학습)
그림 3e에서는 다른 질문/답변 쌍들과 그에 대응하는 앵커들을 보여주며, 그 중 처음 세 가지 예시는 모델의 동작이 우리의 직관과 일치하는 경우, 마지막 예시는 그렇지 않은 경우를 제시
Efficiently Computing Anchors
블랙 박스 모델 $f$, 인스턴스 $x$, 분포 $\mathcal{D}$, 그리고 요구되는 정밀도 수준 $\tau$에 대해 anchor A는 $prec(A)\ge\tau$ 와 $prec(A)\ge\tau$를 만족하는 $x$에 대한 feature predicates의 모든 집합임
$prec(A) = \mathbb{E}_{\mathcal{D}(z|A)}[𝟙_{f(x)=f(z)}]$
임의적인 $\mathcal{D}$과 블랙박스 모델 $f$에 대해, 이것의 정밀도를 직접적으로 계산하는 것은 다루기 힘듦
대신 확률론적 정의를 도입: 높은 확률로 정밀도 조건을 만족하는 anchors
$P(prec(A)\ge\tau)\ge1-\tau$
만약 여러 anchors가 이 평가 기준을 만족한다면, 입력 공간의 더 넓은 부분의 행동을 묘사하는 것을 선호함
→ 즉 coverage가 넓은 것
수식적으로는 anchor의 coverage를 $\mathcal{D}$로부터의 샘플들이 적용되는 확률로서 정의
즉 $cov(A)=\mathbb{E}_{\mathcal{D}(z)}[A(z)]$
→ 전체 데이터에서 샘플들이 A에 포함되는 비율
따라서 이 anchor에 대한 search를 다음과 같은 조합 최적화 문제로 정의:
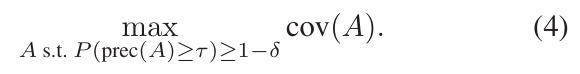
전체 가능한 anchor들의 수는 지수적이며 이는 문제를 정확히 풀기에는 힘듦
anchor에 대한 검색은 확률론적 Inductive Logic Programming (ILP)와 다른 rule-finding method와 비슷한 반면 하나의 핵심적인 차이는 저자는 dataset apriori를 가정하지 않는다는 점임
그 대신 perturbation distributions와 블랙박스 모델이 있어 $\mathcal{D}$아래서 정밀도와 coverage 경계를 구할 수 있음
dataset apriori: 데이터 셋이 미리 주어진 고정된 것
이론적으로는 아주 큰 데이터셋을 생성한 뒤 ILP(Integer Linear Programming, 정수 선형계획법) 같은 방법을 사용해서 앵커(anchors)를 찾을 수도 있음
하지만 그렇게 하려면 매우 많은 수의 변형된(perturbed) 샘플을 만들고, 그 각각에 대해 블랙박스 모델의 예측을 수행해야 하므로 계산량이 너무 커져 사실상 불가능
특히 텍스트처럼 차원이 높고 희소(sparse)한 도메인에서는 이런 접근이 더욱 비효율적임
그래서 모델의 교란(perturbation) 공간에서의 행동을 효율적으로 탐색하기 위해, 우리는 multi-armed bandit(다중 슬롯머신) 문제 설정을 활용함
Bottom-up Construction of Anchors
bottom-up constructions of anchors는 이후에 잠재적 anchors의 공간을 검색하도록 확장됨
저자는 점진적으로 anchor A를 구축하는데 이는 empty rule에서 시작됨
→ 즉 모든 instance에서 적용되는 규칙
매 반복마다 하나의 추가적인 feature rpedicate ${a_i}$를 A에 확장함으로써 수많은 후보 rules를 생성
→ 즉 각 반복의 후보 rules의 집합은 $\mathcal{A}={A \wedge a_i, A \wedge a_{i+1},A \wedge a_{i+2},...}$
여기서 예측되는 가장 높은 정밀도를 가지는 candiate rule을 찾고 A를 선택된 candidate로 교체하며 이를 반복
만약 현재의 anchor가 $P(prec(A)\ge\tau)\ge 1-\tau$를 충족한다면 이 anchor를 선택하며 종료
비록 이 접근이 직접적으로 coverage를 계산하지는 않고 shortest anchor를 찾으려고 하지만 짧은 anchor가 높은 coverage를 가질 가능성이 높고 유저가 이해하기에 가장 쉽다는 것을 저자는 말함
저자는 매 반복 내에서 최고의 candidate를 선택하기 위해서 이러한 후보들의 정밀도를 효율적으로 계산하고 싶음
true precision을 계산할 수 없기 때문에, $\mathcal{D}(\cdot|A)$로부터의 샘플들에 의존하여 A의 정밀도를 측정함
하지만 고정된 수의 샘플들은 정확한 측정에 대해서는 너무 많거나 너무 적음
대신 저자는 최소한의 집합에 관심이 있음
이는 pure-exploration multi-armed bandit 문제로 수식화 될 수 있음
→즉 각 후보 A는 arm이고 A의 true precision은 $\mathcal{D}(\cdot|A)$ 아래에서의 latent reward이며 각 arm A의 당김은 $𝟙_{f(x)=f(z)}$의 평가임
이러한 설정에서 KL-LUCB 알고리즘은 가장 높은 정밀도를 가지는 규칙을 찾을 수 있게 함
알고리즘은 KL divergence를 기반으로 confidence regions를 구축함으로써 작동함
각 단계에서, 알고리즘은 두 개의 구분되는 규칙을 선택함: best mean (A)과 highest upper bound (A’) 그리고 샘플을 $\mathcal{D}(z|A)$와 $\mathcal{D}(z'|A')$에서 가져오고 $𝟙_{f(x)=f(z)}$$𝟙_{f(x)=f(z')}$를 계산함으로써 그들의 bounds를 업데이트 함
이 샘플링 과정은 A의 lower bound가 A’의 upper bound보다 $\epsilon \in [0,1]$ 이내로 높아질 때까지 계속됨
만약 A*이 가장 높은 정밀도를 가지는 arm이라면 다음은 선택된 규칙 A의 true precision을 보장함
$P(prec(A)\ge prec(A^*)-\epsilon)\ge1-\delta$

알고리즘 1은 이 접근의 개요를 보여주는데 KL-LUCB에 의해 선택된 규칙이 anchor인지 평가할 때 이것이 우리의 정밀도 평가를 만족하는 지 확신이 들어야 함
그러므로 $prec_{lb}(A)<\tau$이지만 $prec_{ub}(A)>\tau$인 발견된 규칙 A에 대해 저자는 A가 anchor라는 것($prec_{lb}(A) > \tau$) 또는 아니라는 것($prec_{ub}(A)<\tau$)에 대해 자신이 있을 때까지 $\mathcal{D}(\sdot|A)$로부터 샘플링함
Beam-Search for Anchor Construction
greedy 접근법이 현재까지 short anchors를 찾을 수 있다고 묘사되고 그것을 보증할 수 있음에도 매 단계에서 높은 확률로 그 선택은 최선의 근처였고 이는 두가지 핵심 단점이 있음
- 접근법의 greedy한 특성으로 인해 한 번에 하나의 규칙만 유지할 수 있으며 따라서 suboptimal한 선택은 되돌릴 수 없음
- greedy 알고리즘은 anchors의 coverage와 직접적으로 연관되지 않고 발견한 shortest anchor를 반환함
이러한 문제를 해결하기 위해 greedy approach를 확장하여 beam-search를 수행하도록 함
어떻게?
search가 많은 가능한 anchors 중에서 가장 높은 coverage를 찾아내도록 가이드하는 동시에 candidate rules를 유지
알고리즘 2를 보면 이는 greedy approach와 비슷한 구조이지만 단일 후보 대신 현재 후보들의 B집합 가짐
모든 가능한 candidate들을 만든 후에 multiple arms를 가지는(Explore-m setting) KL-LUCB 접근법을 기반으로 B-best candidates를 선택
정리하자면 저자의 접근법은 beam search로 suboptimal한 anchor도 찾아서 가장 coverage가 높은 하나를 찾는 greedy approach를 사용하여 최적화를 할 수 있었음
실제 실험 파라미터
$B = 10, \epsilon=0.1, \delta=0.05$
Experiments
첫번째로 이전에 소개되었던 Tabular dataset에 대해 3개의 모델(로지스틱, 그래디언트 부스트 나무, 뉴럴네트워크)를 만들고 이를 LIME과 anchor에 대해 비교해봄
LIME과 anchor는 validation set을 통해서 구조화되고 test set에 대해서 precision(얼마나 설명되는가)과 coverage(예측 중 얼마나 맞았는가)를 평가함

Lime은 모든 feature에 대해 가중치 형태의 연속적 중요도를 주는 방식이기 때문에 Anchors와 공정한 비교가 어려움
따라서 저자는 lime이 태뷸러 데이터에서 규칙처럼 행동하도록 변형한 두 버전을 만듦
lime-n(normalized)은 normalize해서 가장 영향력 있는 몇 개 feature만 남기고 나머지는 0으로 만듦 → precision이 높고 coverage가 낮음
lime-t(thresholded)는 top-k개 또는 threshold 이상의 feature만을 선택해서 설명으로 사용 → precision이 낮지만 coverage가 높음(이때 threshold는 공정한 비교를 위해 anchor와 비슷한 precision을 가지는 threshold로 지정)
결과는 precision에서는 앞도적인 성능을 보이지만 coverage측면에서는 확실한 우위가 없었음
따라서 이는 비현실적으로(threshold를 완벽히 조정한) LIME 버전이라 해도 Anchors보다 뛰어나지 않을 수도 있음을 보임

Figure 4에서 gb에 대한 coverage를 두 개의 데이터셋에 대해서 보여줌
submodular pick(SP-LIME과 SP-Anchor)에 의해 선택되거나 랜덤하게 (RP-LIME과 RP-Anchor) 선택된 더 많은 explanations를 유저가 볼 수록 어떻게 되는 지를 실험
→SP 설명 간 중복을 최소화하면서 커버리지를 극대화하도록 선택, RP 설명을 무작위로 선택
결과는 랜덤 설명들의 평균 coverage가 낮은 반면(rcdv에서 4.8%), submodular pick의 explanations의 집합은 모델의 글로벌한 행동을 이해시킬 수 있음(10개 이상시 ~50%이상)
방법론적으로 보면 비슷한 precision임에도 불구하고 더 높은 coverage를 anchor 접근법이 보여줌
User study
유저가 explanations를 보고 unseen instances에 대한 모델의 행동을 예측할 수 있을까?
adult와 rcdv 데이터 셋에 대해서는 (1) 10개의 예측들을 explanations를 제외하고 보게 하고
(2) explanation이 있는 예측을 한개 보거나 (3) 2개의 explanations가 있는 예측을 보여주는 경우
3방법으로 진행
user들은 자신이 있으면 답을 작성하고 모르겠으면 “I don’t know”를 작성하도록 함
“I don’t know”의 선택 여부를 coverage 측정으로 활용함
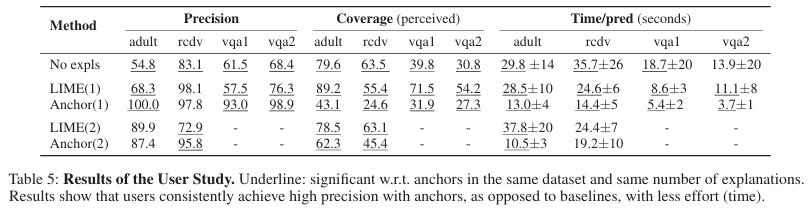
coverage는 1개에서 2개로 넘어갈 때 일관적으로 증가함을 보였음
LIME의 성능은 태스크에 따라 변동이 있었음 특히 VQA에서 설명이 없는 것보다 더 나쁜 성능을 VQA1에서 보였음
Anchor의 경우 확실하게 정답을 맞춤(precision 높고 coverage 낮음)
또한, anchor를 사용할 때 이해하는 데 훨씬 더 적은 시간이 걸림
설문 조사에서는 21/26 비율로 anchor를 더 선호했고 24/26은 anchor를 가지고 하면 더 정확해진다고 답함
LIME이 더 정확해진다고 답한 2명은 실제로는 anchor를 가지고 더 높은 정확도를 보였음
Limitations and Future Work
Overly specific anchors: 경계선 근처에서의 예측 또는 rare classes에 대한 예측은 매우 특정한 조건들이 필요로 하고 이는 anchor를 복잡하고 낮은 coverage를 가지게 함
Potentially conflicting anchors: anchor접근법을 “in the wild”하게 사용할 때, 같은 테스트 instance에 대해 2개 이상의 anchors가 다른 예측을 만들 때가 있음
이는 두가지 이유에서 비롯됨 (1) anchor가 만들어질 때 높은 확률로 precision guarantee하도록 됨 (2) 선택 과정에서 submodular objective이 anchors 집합으로 하여금 낮은 overlap을 가지도록 함
→precision의 threshold를 높이는 것을 제안함
Complex output spaces: output이 구조화되고 복잡하다면 다양한 설명들이 유용함. 저자는 연구에서 출력의 특정 함수에 대한 설명을 제공했지만 전체 output space에 대한 설명은 future work로 남겨둠
→예를 들어서 왜 “play”를 noun으로 예측했는가에 대해서는 설명하지만 왜 noun일 확률이 0.7이고 verb일 확률이 0.1이고 ~이런 전체 결과를 해석하지는 못함
Realistic perturbation distributions: explanation 모든 교란 기반 설명 기법은, 모델의 동작을 드러낼 만큼 충분히 표현력 있는 동시에, 해석 가능한 구성요소 위에서 작동하는 지역적 교란 분포(local perturbation distribution)에 의존함
→ 너무 교란이 복잡하면 해석하기 어렵고 너무 단순하면 모델의 진짜 동작을 알 수 없음
하지만 이런 적절한 분포를 찾는 일은 일부 도메인에서는 여전히 어려움
예를 들어, 이미지의 경우 교란을 통해 어떤 통찰을 얻을 수는 있었지만, 그 설명들을 이미지 간에 비교하는 것은 불가능했음
→이미지 분야에서는 superpixel을 지우거나 흐리게 하는 식으로 perturbation을 사용하는데 이는 한 장의 이미지 내에서는 의미가 있어도 다른 이미지들 간의 일관된 비교 기준을 제공하지는 못함

