[2025-2] 박제우 - GRAPH ATTENTION NETWORKS

https://arxiv.org/abs/1710.10903

Graph Attention Networks

 

 

1. Introduction

현재까지 CNN은 grid-like structure에서 높은 성능을 발휘했고, 이는 이미지 분류나 기계 번역 등에서 쓰였다. 그러나 현실세계의 문제는 단순히 grid로만 표현될 수는 없다.

 

Graph Neural Network는 이러한 맥락에서 소개되었는데, 보다 일반화된 RNN구조를 사용했다. GNN은 반복적인 과정을 포함하는데, 이 과정은 노드를 평형 상태에 이를 때까지 전파한다. 그 후 각 노드의 상태를 기반으로 출력을 생성하는 신경망이 뒤따른다.

 

그럼에도 불구하고, 이러한 그래프 도메인에 합성곱(convolutions)를 적용하려는 시도가 계속되어 왔는데, 이는 Spectral Approaches와 Non Spectral Approaches로 나뉜다.

Spectral Approaches : 그래프의 라플라시안 행렬을 만들고 이를 Eigendecomposition 한다는 연산량의 한계, 또한 라플라시안 고유벡터는 그래프 구조가 살짝만 달라져도 크게 달라진다는 한계가 있다.

Non Spectral Approaches : 그래프 위에서 직접적으로 합성곱을 정의하며, 공간적으로 가까운 이웃들로 구성된 집합에 대해 연산을 수행하는데 대표적인 방식으로는 GraphSAGE 등이 있다. 이러한 방식은 Spectral 방법에 비해 더 나은 성능을 보여줬다.

 

Attention Mechanism의 장점은 현재까지 Sequence task에서 거의 표준이 되어왔다. 또한 지난 Attention is All You Need 논문에서는 Self Attention이 SOTA를 달성할 수 있다는 것을 증명했다.

 

따라서 본 연구는 그래프 구조에서 노드 분류 작업을 위해 Self - Attention 기반의 모델을 소개한다. 이 모델이 갖는 장점은 다음과 같다.

    1) 노드-이웃 쌍 간의 연산 병렬화 가능

    2) 서로 다른 차수를 가진 노드들에도 적용이 가능

    3) 제로 샷 상황에서 효과적이다.

 

2. GAT Architecture

Single Graph Attention Layer

N이 노드의 개수, F가 feature의 차원일 때, 입력은 다음과 같이 정의되고 이는 각각 h’을 생성한다.

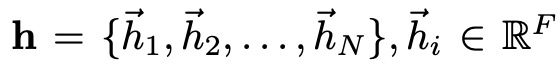
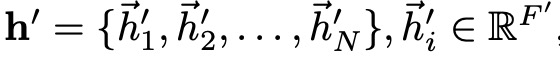
입력 피쳐를 더 표현력 있는, 즉 고차원의 표현으로 바꾸러면 최소 1개의 선형 변환이 필요하다. 이는 learnable weight를 통해서 projection 된다. 이 후 이렇게 선형변환된 각 노드들에 대해 Self Attention을 수행한다.

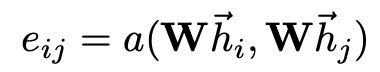
다음과 같이 Self Attention을 수행하면 노드j와 노드i의 중요도를 볼 수 있다.

 

원래 순환 신경망 구조에서는 병렬 연산을 통해 모든 노드에 대해서 Attention 계산을 수행할 수 있지만, 그래프 구조의 경우는 상호 연결된 노드 사이에서 연산해야 하기 때문에 Masked Attention을 수행한다.

 

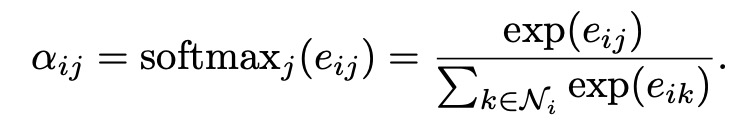
여기서 Ni는 노드 i의 이웃을 말한다.

LeakyReLU 비선형함수까지 추가한 전체 Attention 계산 수식은 다음과 같다.

 

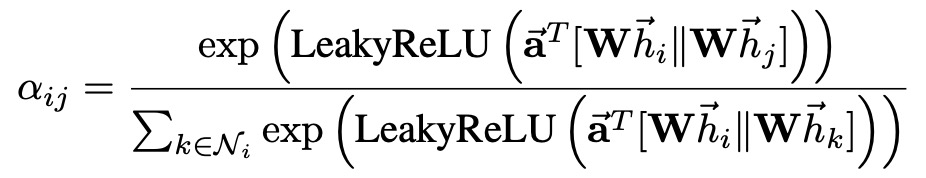
다음 그래프는 각 노드에 대해 어텐션이 계산되는 과정을 도식화한 것이다.

 

 

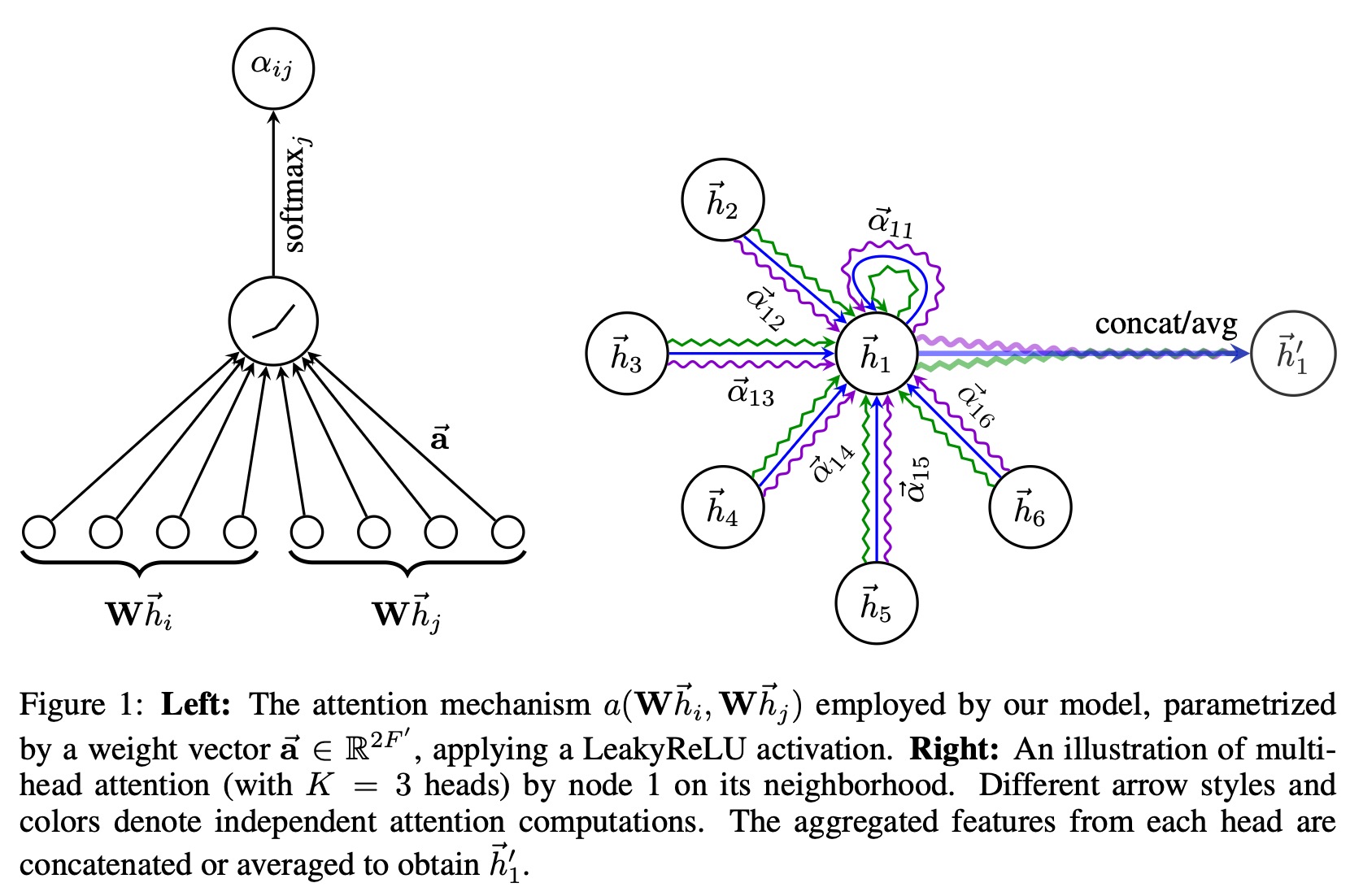
왜 Multi Head Attention이 필요한가?

이는 2017년 Transformer의 아이디어와 유사하다. 다음 수식은 GAT의 중간 히든 레이어에서 사용되는 Multi Head Attention 수식이다.

히든 레이어는 Multi Head Attention의 결과를 Concat함으로써 표현력을 더 확보하게 된다. 여기서 K는 Head의 수가 된다.

 

 

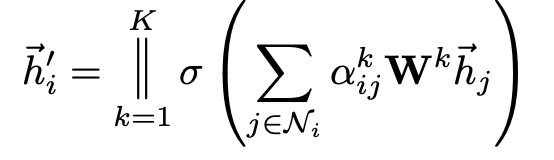
다음 수식은 마지막 레이어에서 Multi Head Attention 적용 방식을 나타낸다. 최종적으로는 Concat했던 Multi Head의 계산 결과를 평낸 뒤 비선형 함수를 적용한다.

 

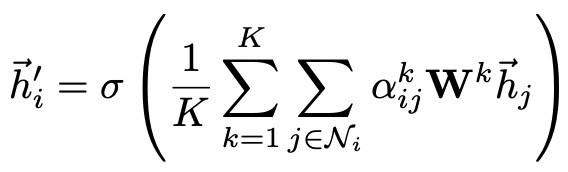
기존 연구와의 비교

계산 효율성 : Self Attention은 모든 노드-이웃 쌍에 대해 병렬 처리를 할 수 있기 때문에 시간 복잡도가 감소한다. GCN에 비해 Eigendecomposition이 불필요함에도 불구하고 GCN과 비슷한 시간 복잡도를 보인다.

가중치 차별화 : GCN은 이웃에 동일한 가중치를 부여했으나 GAT는 선형 변환 하면서 이웃 노드마다 다른 Attention Weight를 부여할 수 있음.

GraphSAGE는 샘플링을 사용하지만, GAT는 이웃 전체를 활용할 수 있다.

 

 

3. Evaluation

기존의 GNN기법들과 비교했을 때, 4개의 대표적

인 그래프 기반 벤치마크에서 평가되었다. 실험 결과 대부분 SOTA를 달성할 수 있었다.

 

각 전이 학습과 귀납 학습에 대한 실험 결과는 다음과 같고 비교 모델에서 가장 높은 성능을 보였다.

 

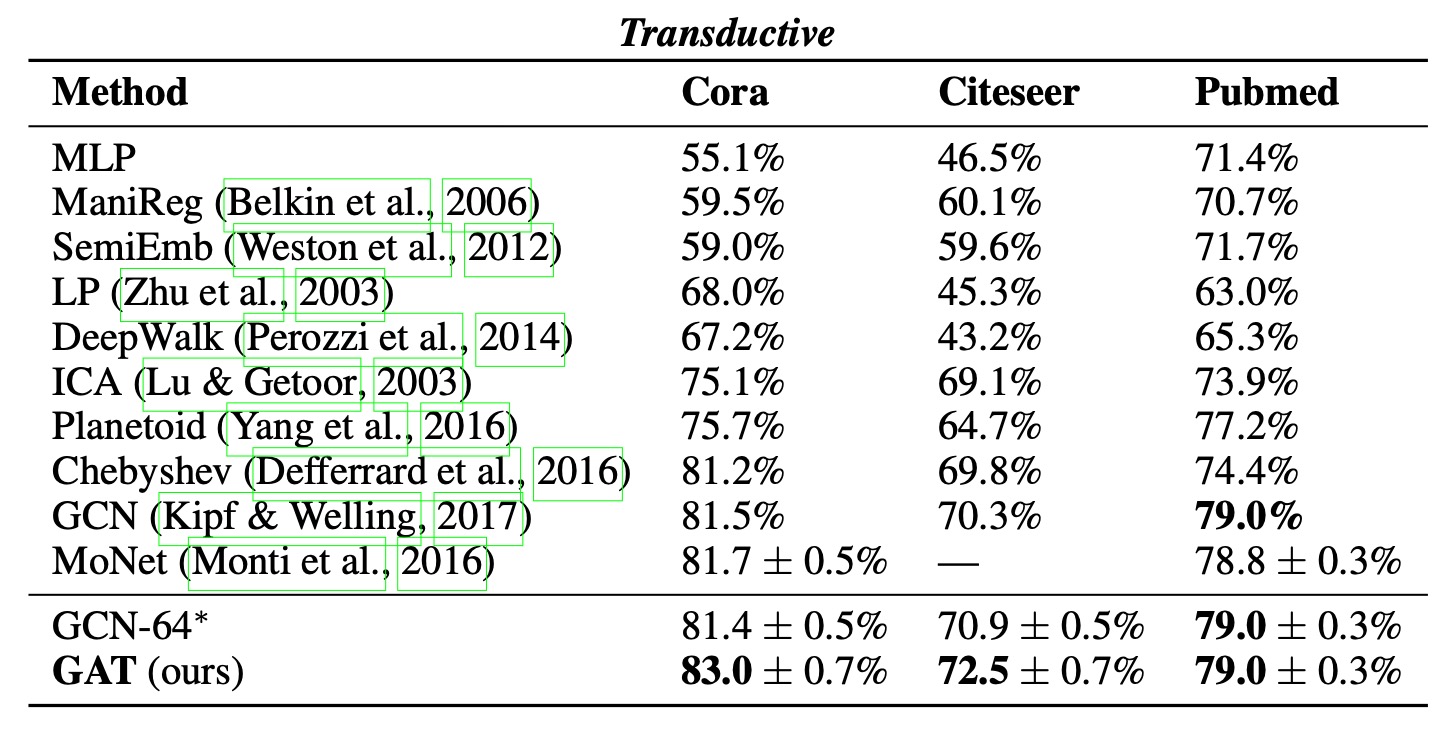
먼저 전이 학습을 위해 비교한 모델은 다음과 같다.

Label Propagation (LP)

Semi-Supervised Embedding (SemiEmb)

Manifold Regularization (ManiReg)

DeepWalk (그래프 임베딩을 위한 skip-gram 기반 방법)

Iterative Classification Algorithm (ICA)

Planetoid

GCNs (Kipf & Welling, 2017)

Chebyshev 필터 기반 그래프 컨볼루션 모델 (Defferrard et al., 2016)

MoNet (Monti et al., 2016)

 

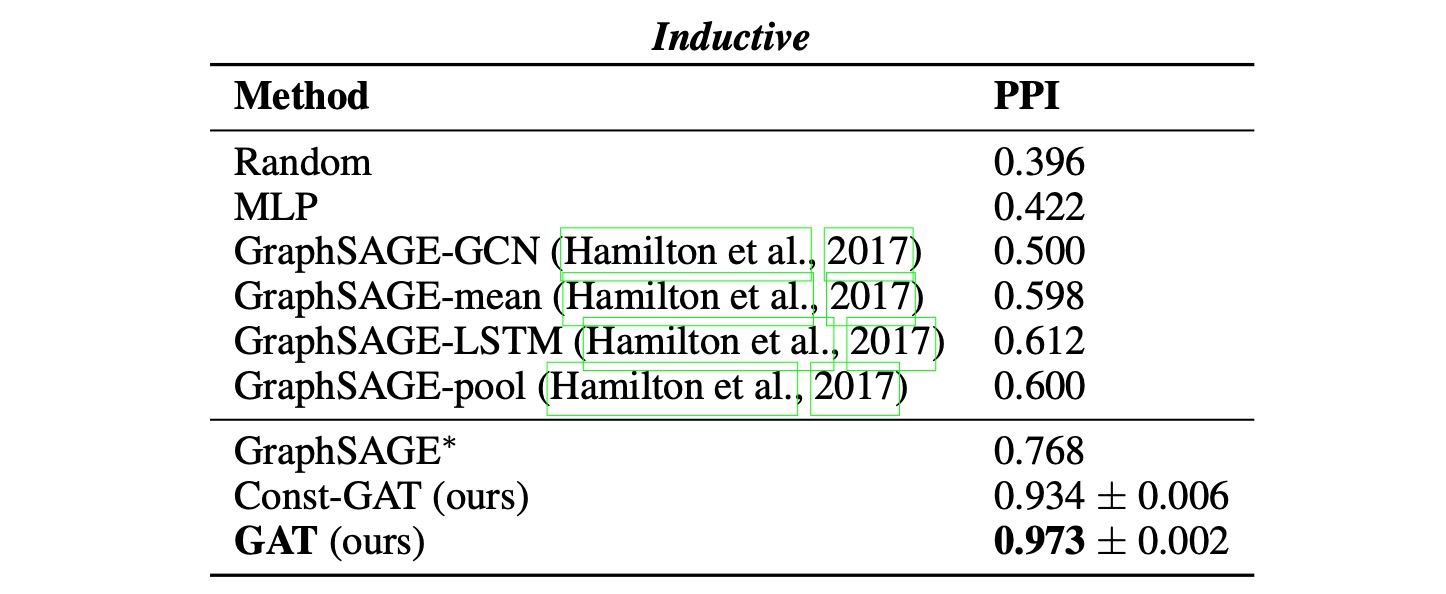
귀납 학습에서는 4가지의 GraphSAGE모델과 비교되었다.

GraphSAGE-GCN: GCN 스타일의 연산을 귀납 학습 환경에 확장한 모델

GraphSAGE-mean: 이웃 노드의 특징 벡터들의 평균값을 취함

GraphSAGE-LSTM: 이웃 노드의 특징들을 LSTM에 입력해 집계

GraphSAGE-pool: 특징 벡터에 MLP를 적용한 후 elementwise 최대값을 취함

 

Cora 데이터셋의 결과를 tSNE로 시각화한 결과는 다음과 같다.