Variable Selection via the Sparse Net
Variable Selection via the Sparse Net
Variable selection is an important problem when the model includes many noisy variables. For years, the sparse penalized approaches have been proposed for the problem. Examples are the least absolute selection and shrinkage operator (LASSO) and smoothly cl
www.kci.go.kr
0. Abstract
- 모델 내 노이즈가 많은 변수에 대해, 변수 선택은 중요하고 어려운 문제이다. 이러한 상황에서의 변수선택을 위한 방법으로, LASSO, smoothly clipped absolute deviation penalty(SCAD) 등이 존재하였음.
cf) LASSO 회귀 식을 살펴보면, 무조건 최적의 beta 값만 찾는 것이 아니라, 계수에 대한 L1 패널티를 주어, 패널티를 포함한 식을 최소화하는 계수를 이용하는 regression(회귀분석)

기존의 MSE를 최소화하는 LSE 방정식을 사용하는 regression에서 bias – variance trade off 관계를 반영하여 약간의 bias를 얻더라도, variance를 많이 낮출 수 있어서 사용. 위에서 설명에서 노이즈가 많은 경우 모델의 안정성이 떨어져 variance가 높게 나타나므로, 이를 해결하기 위한 lasso ridge 등 L1, L2 패널티를 주어, 모델의 성능을 높이려는 시도에 해당함.
1. Introduction

linear regression을 고려해보자(선형회귀 모형)
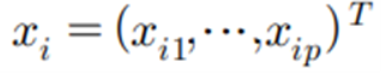

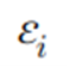
이때, noise가 많은 변수를 모델이 포함하면, 변수 선택은 굉장히 중요한 문제 중 하나이다. tradional한 변수 선택으로는, best subset selection에 기반한, forward selection과 backward elimination 방법이 전통적으로 사용되었었음. 그러나, 이러한 방법은 방대한 양의 계산과, sampling properties의 불안정성 등과 같은 치명적인 결함이 존재하였다. 이에 대한 논의로

LASSO regression이 논의 되었음. 이때 J_lambda term은 모델의 복잡도를 나타내는 tuning parameter에 해당함. 다양한 통계분야에서 패널티를 다양하게 확인 가능한데, 대표적으로 LASSO는 필요한 변수는 선택하는데, 상수의 bias가 추가된다.
ridge는 L2 패널티, lasso는 L1 패널티를 포함하고, ridge 와 lasso의 중간인 Elastic Net(ENET)방식이 존재하곤 했다.
이 논문에서는 새로운 패널티인 sparse Net (SNET) 을 제안하는 바이다. (for linear regression.)

SNET은 Elastic Net에서의 아이디어와 비슷하지만, 3가지의 다른 차별점을 두고 있다.
SNET은 불필요한 bias 추가가 나타나는 음의 ridge effect를 개선하였다.
ridge parameter의 선택에 따라 잔차 제곱 패널티의 합이 오목하거나 볼록할 수 있어서, sample size가 커짐에 따라 최소화 되는 지점이 존재하게 된다.
음의 ridge 효과에 의해 패널티가 볼록하지 않게 되고, 이때문에, 희소성(즉, 적은 수의 변수를 선택하게 됨)이 더 높게 나타난다. 희소성이 더 좋다는 것이, 이 논문에서의 수치 실험으로 나타난다.
2. Sparse Net
2.1. Definition

위의 식이 기존의 ENET에서의 식인데, 이 식을 보면 패널티가 둘다 non-zero이기 때문에, 예기치 못한 상황에서 large bias가 나타나서, lasso보다도 더 많은 변수를 선택하는 경우도 존재함. 이를 해결하기 위해 패널티 주는 방식에서 lambda 2 를 –로 바꿈. (ridge의 negative 효과를 제공)

음으로 식을 바꾼 SNET을 살펴보면, ENET보다 적은 bias를 가지게 되고, 더 희소성(적은 변수를 선택)을 가지게 됨. 위의 식은 일반적으로는 비볼록하지만, 람다2가 design matrix의 최소 eigen value보다 작은 경우에는 convex하게 나타난다. 이 논문에서는 확인하지는 않았지만, 희소성조건하에서 다른 논문아이디어를 따와 이론상 global minimizer가 될 것을 기대할 수 있음.
또한, lambda2의 값을 조정함으로써, 오목함을 제어할 수 있어서 SCAD와는 다른 특징이 나타나고, numerical 연구에 따르면, SCAD보다 더 적은 변수를 선택하는 것을 확인할 수 있음.
2.2. Orthogonal design study
람다1, 람다2의 역할을 설명하기 위해 직교하는 design matrix상황을 고려해보자.
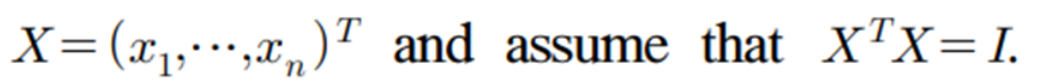
위의 가정하에서, 아래식을 직접 유도해보았다.


이 loss function을 최소화 하는 것은 각 원소들에 대해 최소화 하는 문제가 되고, design matrix에서의 1열(상수 term 혹은 절편) 을 무시하면, LSE는

이 된다. 비슷하게, 패널티를 준 LASSO는

을 최소화 하는 것과 동일하다.
이것의 해는

이와 같은데, SNET은


해는 위의 식과 동일하다. 이는 beta 추정값에서 람다1/2 값으로 shrinkage효과를 주고 있는데, SNET은 동시에 1/(1-lambda2)효과로 회귀 계수를 상승시키기도 한다.
ENET에서,

이 식에서 람다1, 람다2가 모두 베타 값을 감소시키는 패널티만 주는 것을 확인 가능 이때문에, ENET은 rescaling과정이 필요
2.3. Computational algorithm

convex, concave 두 함수로 나누어

위의 식을 최솟값으로 수렴할때 까지 computational 계산을 수행함.

최적의 beta 값 구해가는 알고리즘. closed form이 없어서 수렴할때까지 알고리즘 적인 계산 수행. 최솟값으로 수렴할때까지
3.1. Simulation studies
다변량 정규분포를 따르는 x와 다변량 정규분포 공분산이 r^|j-k| 인 경우를 가정
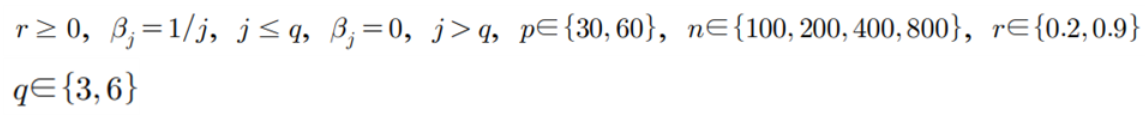
1) 1000개의 독립적 test sample prediction에 대한 MSE 계산
2) non-zero estimate값을 정확히 맞춘개수와 3)부정확한 개수
총 3가지의 measure를 사용


4. Concluding Remark
이 논문에서 새로 제안한 패널티인 SNET이 선형 회귀 모델에서 변수선택 및 파라미터 추정에서 활용될 수 있음을 보여주었고, numerical 실험을 확인해보면, 높은 예측 정확도를 보이고, 또, 희소한 모델 즉, 불필요한 변수를 덜 선택하는 모델을 생성함을 알 수 있고, 또, SNET의 계산 알고리즘은 단순히 LASSO를 해결하는 방식의 반복일 뿐이라 computational 이점이 있음을 알 수 있다.




