https://peerj.com/preprints/3190.pdf
Forecasting at Scale
Facebook의 prophet 논문 리뷰
1. Abstract
● 예측(forecasting)은 데이터 사이언스에서 중요한 업무중 하나
● 중요성에도 불구하고, 다양한 분야의 시계열 분야가 존재하고, 시계열 분석 전문가가 희귀함
● 목적 : 해석이 가능한 parameter(모수), domain지식이 있는 사람은 직관적으로 조절가능하게 하는 모형(시계열 분석에 대한 전문성이 떨어지더라도)
2. Introduction
문제점
● 완전한 자동예측 기술은 flexibility가 떨어져서, tuning하기 어렵고, 적절한 가정을 포함하기 힘듦
● 도메인 지식이 깊은 전문가가 시계열에 대한 이해가 떨어지는 경우가 많음
● 고품질 예측에 대한 수요가 높은데 반해, 예측 생산은 그에비해 느림
1) 시계열에 대한 교육 없이도, 사용가능한 적합한 모델
2) 잠재적 특성들을 시계열 모델에 반영가능
3) 모델 평가, 모델 수정 자동화

● 대규모 시계열 예측 계산등은 큰 문제가 아니고, 병렬로, 관계형 DB에 저장되어 큰 어려움은 아닌데, 다양한 예측에서의 복잡성 및 예측에 대한 신뢰를 구축하는 것이 더 어려운 일임.
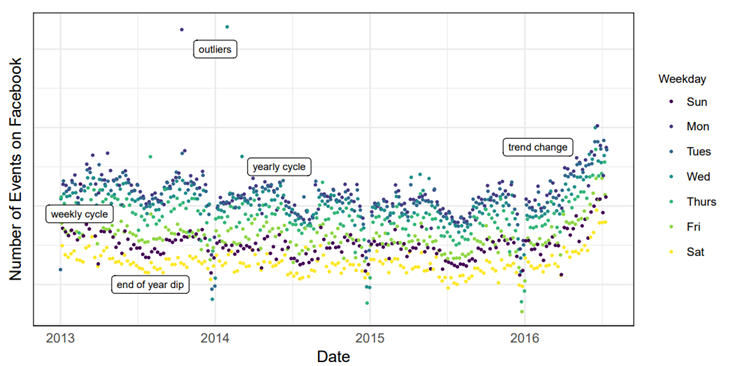
2 Features of Business Time Series
● 위의 그림에서는 페이스북에서의 이벤트 생성 수를 시각화, 몇가지 뚜렷한 계절적 효과를 확인할 수 있음. 주간, 연간 차이, 크리스마스나, 새해 주변에서의 하락성이 나타나고, (2017년 기준) 최근 6개월은 이전과는 다른 변화가 관찰됨.
자동 ARIMA 모델을 적합에서는, 경향이 변경되는 경우에 추세 오류가 크게 나타나고, 계절성 역시 반영하지 못하는 모델임.
● 자기회귀 구성요소 / 이동평균 구성요소 등 조정이 필요한데, 이는 시계열에 대한 이해가 부족한 사람은 다루기 힘든 모델이라는 단점이 존재함.

기존의 모델들로 적합했을때의 결과들임. 위에서부터, 여러 ARIMA모델 중 최적, 지수평활모델, 주간계절성, 주간 + 연간 + 계절성 반영 모델
3 The Prophet Forecasting Model

● 추세, 계절성, holiday 3가지로 decomposition 하여, 3가지요소가 더해져서 y를 예측
● g(t)는 시계열의 비주기적인 변화에 대한 모델링
● s(t)는 주기적인 변화에 대한 모델링(주간, 연간 모델링)
● h(t)는 잠재적으로 발생하는 불규칙한 변화 모델링(휴일- holiday)
● 오차항은 모델에 수용되지 않은 변화 – 정규분포를 가정
cf ) 기존의 선형 모델링(논문 외) – GLM : generalized linear model
선형회귀, 로지스틱 회귀분석 등등 predictor와 response 사이의 선형적인 관계를 이용해서 예측하는 통게적 모델링 방법
● GAM 모델링(generalized Additive model)과 비슷.
● non-linear 성향을 파악하는데 용이
● 시간만을 비선형 요소로 이용하지만, 여러 부분을 이용 가능
cf) 추가(논문 외 내용)
predictor를 그대로 사용하지 않고, predictor에 특정 함수를 씌운 상태로 더해서 모델링하는 기법 – 더하는 모델이기 때문에 decomposition이 쉽고, GLM에서는 분포가정이 강력하게 들어가고, 기본적으로 선형 모델링이 기본적으로 깔리는데, GAM은 GLM보다는 좀더 non-parametric한 방법으로, 비선형 관계에 있는 모델링도 적용가능한 모델을 말함
● 유연성이 좋고, 새로운 계절성이 발견되었을 때, 새로운 구성요소를 추가하기가 쉬움.(요소들을 더해가기때문) + 다양한 가정들을 분석가가 추가하기 편한 모델임
● 측정값이 규칙적인 간격일 필요 없음.
● 회귀분석 경험이 있으면, 누구나 쉽게 적용이 가능하고, 해석이 간편하며, 여러 가정들을 추가하기 쉬운 flexible한 모델이기에 다루기 편함
3.1.1 Nonlinear, Saturating Growth
● g(t) : 시계열의 비주기적 변화 모델링 이때, nonlinear(상한 하한등이 정해진경우)
● picewise logistic growth model 적용 + 약간의 식 변형
● g(t) = C / (1 + exp(−k(t − m)))
● C : 한계를 나타내는 carrying capicity
● K : 성장률
● m : offset – 초기값 (시작지점)
● 상한 / 하한의 값이 정해진 경우의 모델링에서의 사용되는 로지스틱 함수
1) c가 상수가 아닌경우 : 인터넷 접속 유저가 점점 늘어나게 되어, 상한 하한에 해당하는 c값이 상수가 아님을 반영해야함
ex) 페이스북 접속자 예측모형에서의 상한 : 전세계의 인터넷 접속가능 인원 수 / 시간에 따라 인터넷 접속 가능 유저의 수가 늘어남으로 상한이 상수값 c로 표현되지 못함.
2) 성장률을 나타내는 k 값이 일정하지 않음을 고려해야함
이를 반영한 모델링 식 – piecewise logistic growth model

간단히, s개의 성장률 변화시점이 있다고 하였을 때, a(t) 는 0,1 로 이루어진 binary 형태로, 특정 시점 이후에는 활성화시켜주는 역할로, a(t)가 1이면 해당시점 이전의 changepoint의 값을 반영, 0이면 반영 x
--> s개의 growth rate change point를 모델링에 포함시키고, C값이 상수가 아니므로 t에 의존하는 함수로 적용시킨 모델링 식의 결과
C(t)의 경우에는 외부데이터 가져와서 적용도 가능하고, 분야별로 적용가능
3.1.2 Linear Trend with Changepoints
● g(t) : 시계열의 비주기적 변화 모델 링 이때, linear한 경우
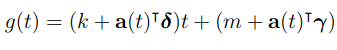
● 상한과 하한이 정해지지 않기 때문에, linear한 modeling
3.1.3 Automatic Changepoint Selection
● 변경점 모델링 sj는 이벤트 날짜등 적용하여 사용가능
● 델타(각 변화점의 변화율)에 대해 라플라스 사전분포 가정 / 타우가 0에수렴하면할수록, 표준 로지스틱/ 선형 growth modeling에 가까워짐.
● 분야별로 특별한 사건에 따른 변화율이 작을수록, 기존 로지스틱, 선형 모델링의 형태
cf) 라플라스 분포는 정규분포와 비슷한 형태를 띄지만, 가운데가 더 뾰족한 형태의 분포이다.
3.1.4 Trend Forecast Uncertainty
● 과거 데이터에서 유추된 분산으로, 타우를 추정값으로 사용하고, 미래의 변화를 예측하는데 사용함.
+ flexibility를 changepoint를 통해 제공
3.2 Seasonality
● 휴가일정이나, 주 5일 근무 등 인간 행동의 결과로 나타나는 주기성 모델링
푸리에 급수를 통해 주기적 패턴에 대한 근사

● P는 주기(P = 7이면 1주가 주기인 경우)
● N은하모닉의 수로, 클수록 패턴을 세세하게 확인함
주간 : N = 3
연간 : N = 10
에서 성능이 good으로 나타남
3.3 Holidays and Event
● 휴일은 주기적인 형태가 나타나지않으므로 부드러운 모델링은 아님
음력을 따르는 휴일이나, 특정이벤트들은 완전한 주기성은 아님. 국가별로 다양한 휴일(중요한역할)등은 매년 효과가 비슷하니, 모델링에 포함시켜야함.
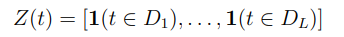

● 각 휴일을 Di라 하고, (영향주는 범위 각 휴일별로 설정가능)
● κ ∼ Normal(0, ν^2). 사전분포를 가정하여 모델링
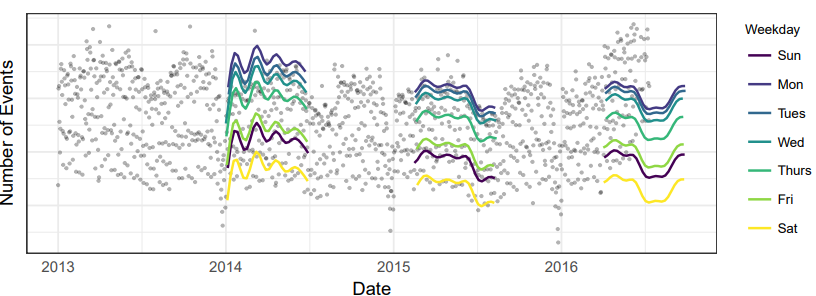

fitting
● 시간데이터만을 활용한 modeling
● 주단위, 연단위 주기성 포착 good
● 1년만 예측할때에는 overfitting 문제가 있기도 하지만, 아래의 전체데이터 피팅한 결과는 잘 맞는게 보이고, 이후의 predict(점선)값들.
3.5 Analyst-in-the-Loop Modeling
● 모델링 자체가 GAM(generalized Additive Model)
이기 때문에, (t에 대한 함수를 씌운 후 더하는 형태) 각 요소들을 분해(decomposition)하기가 쉽고, 이때문에 각 요소들에 대한 tunning 및 가정 적용하기가 쉬운 모델임. 따라서, 도메인 지식이 있는 경우에 이미 분해된 요소의 parameter 등을 수정하는 것으로 시계열 지식이 부족해도 적용이 쉽다는 장점을 가지게 됨.
나타나는 패턴에 대한 설명력 부분이 굉장한 장점 중 하나임.
● 기존의 완전 자동화 예측 / 분석가의 판단이 들어가며, 필요할때는 자동화시스템을 돌려가기 가능

4 Automating Evaluation of Forecasts
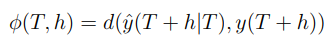
● 특정일의 큰 값은 outlier일 가능 / 때때로 제거하기도.
● 특정 끊임점의 존재 > changepoint를 추가하는 식으로 모델 수정이 가능
5 Conclusion
● 기존의 수동처리보다 많은 예측을 수행 가능.
● 분석가가 분야에 따라 구성요소 선택 / 조정이 가능
● 예측 정확도를 측정 / 추적하며, 분석가가 점진적으로 개선을 이루어감.
● 간단 / 조정이 가능한 모델 / 대규모 예측 가능




