[2023-2] 염제원 - Topology of Learning in Artificial Neural Networks

https://arxiv.org/abs/1902.08160

Topology of Learning in Artificial Neural Networks

 

Abstract

• Neural Network의 학습과정을 Topological Data Analysis의 방법을 이용해 분석함.
• MNIST 데이터셋에 간단한 Feedforward Neural Network를 학습시켜서 가중치의 발전 과정을 분석함.
• 가중치를 0으로 초기화했을 때, 결과는 반복적으로 분화하는 트리 형태로 나타남. 
• 가중치를 작은 어떤 값으로 초기화했을 때, 가중치들은 2D 평면 위에서 부드럽게 발전함.

Introduction

• DNN이 많은 곳에서 활용되고 있으며, labeled된 방대한 데이터셋에 학습 파라미터를 조정하며 학습하는 과정을 통해 이미지 분류, 음성 인식, 번역, 게임 등에 활용이 되고 있음.
• DNN의 학습에 사용되는 각 레이어는 입력 픽셀의 간단한 조합에서부터 시작하여 점차 복잡한 feature를 학습함.
• 그렇지만 DNN은 이론적으로는 많이 이해되지 못하고 있음. 가장 거대한 질문은 왜 이들이 학습을 잘하며 Scalability가 높은지에 대한 내용임. 
• 이 논문의 핵심 아이디어는 모델 학습 과정을 위상적으로 잡을 수 있다는 것에서 출발함.
• Neural Network의 각 레이어에 대해 각 학습 Step에서의 이들의 뉴런들을 가중치를 갖는 벡터로 생각하여 결과적으로 고차원 벡터공간에서의 point cloud를 구성함. 

From point clouds to graphs

• Data Science에서 Dataset은 Feature 마다 각 Observation이 있는 것으로 묘사됨.
• 각 Data는 각 Feature 마다 하나의 차원을 형성하게 됨.
• 결론적으로 Dataset은 Feature Space에서의 point cloud를 형성함.
• 목적은 Point Cloud가 가지와 같은 흥미로운 모양을 갖느냐를 확인하는 것임.

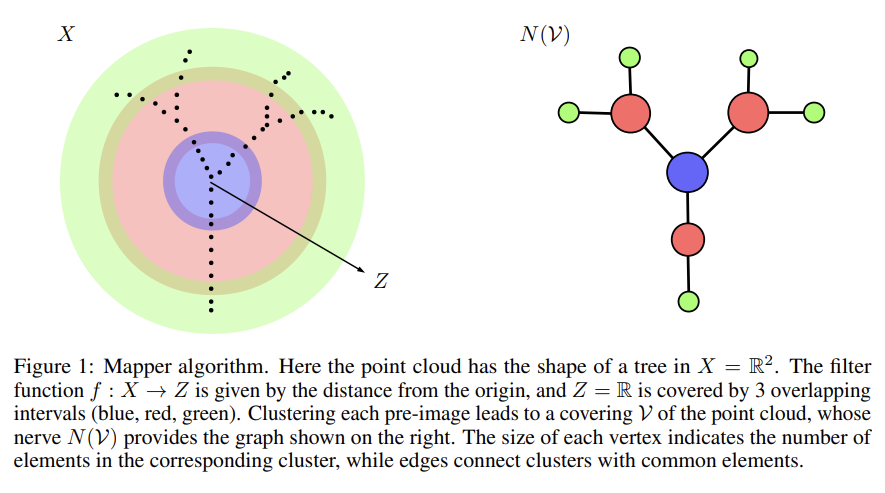
Mapper Algorithm

• 고차원 Feature Space에서의 원본 Point Cloud의 위상적 성질을 포착하는 그래프를 구성하는 알고리즘.
• Feature Space X에서의 Point Cloud에 대해 Mapper Algorithm은 가장 먼저 Space Z로의 연속인 mapping f:X->Z를 결정하는 것을 요구함. 
• 이 Map은 Filter Function으로 불리며, 예를 들어 X의 부분공간으로의 사영 사상도 Filter Function으로 볼 수 있음.
• 다음은 Z의 Finite Open Covering U={U_i}를 찾는 것임.
• 군집화 알고리즘을 활용하여 U_i의 역상 f^-1{U_i}에 대해 각각 적용이 되어, Point Cloud의 Open Covering V={V_j}를 구성할 수 있음.
• 최종적인 Mapper Graph는 V의 nerve라고 불리며, 이는 교집합이 공집합이 아닌 index set J를 갖는 J의 부분집합 K의 집합으로 볼 수 있음. N(V) = {K in J such that Intersection of k in K V_k != empty set

Learning graphs

• Fully Connected Feed Forward Neural Network의 각 Layer의 학습 과정을 보여주는 Mapper Graph를 만들었음.
• 각 i번째 layer의 N_i개의 뉴런에 대해, 각 뉴런에 들어오는 weight의 변화를 트래킹함. 즉, i-1번째 Layer와 i번째 Layer 사이에 대응하는 Weight Matrix의 Column을 고려하는 것임.
• 실험은 minibatch를 활용한 SGD를 사용했음.
• 각 Training Step마다 N_(i-1) 크기를 갖는 N_i개의 weight vector (N_(i-1) 차원 공간의 N_(i)개의 점들)을 기록함.
• Training이 끝나면, n_steps * (N_i)개의 N_(i-1)차원 벡터들의 point cloud를 얻을 수 있음.

Symmetric initialization and branching trees

• 학습 과정에서 가중치의 발전은 종종 branching하는 트리 모양을 띰. 여기에서는 L2 norm을 Filter Function으로 활용하고, DBSCAN을 군집화 알고리즘으로 활용함.
• 학습 초기에는 가중치들은 같은 경로에서 발전하는데, 이후에 서로 다른 방향의 두 경로로 나뉨. 가장 처음의 분화 과정에서 가장 급격한 정확도의 증가가 일어남. Output Neuron이 10개인 만큼 계속 분화가 발생함.
• 분화 과정에 따라서 모델의 식별 능력은 상승함.
• Hidden Layer의 뉴런들도 비슷한 과정을 띰. 각 가지마다 대부분 같은 시간에 다른 가지로 분화하는 특성을 띰. Output Layer와 달리 Hidden Layer의 Neuron에 대한 최종 발전 가지 개수는 Hidden Neuron의 개수와 같지 않음. 여기에서는 100개의 Hidden Neuron을 사용했으나 12개의 가지만 발견이 되었음. 이것은 Hidden Layer의 Neuron 개수가 몇개까지가 효과적인지를 생각해볼 수 있게 함.
• 그렇지만, 에폭 수를 늘리다 보면 더 분화를 하는 경향이 있는데, 언제 Maximal Branching이 되는지를 탐구하는 것도 좋은 연구 주제가 될 수 있다고 제안함.

 

Tiny random initialization and learning surfaces

• 각 가중치를 N(0, 10^(-6))의 random 분포에서 뽑아서 결정하고, MNIST의 학습과정을 각 Neuron에 대해 구했음.
• Output Layer의 가중치들은 zero initialization의 case와 유사한 발전 과정을 거쳤음. Branching Phase와 함께 Tree에서 총 10개의 서로 다른 숫자를 의미하는 Branch로 분화함.
• 첫번째 Hidden Layer의 학습 과정이 가장 흥미로웠음. (Figure 6) 동시에 분화가 일어나고 smooth surface에서 평행하거 발전이 진행됨. 그 이후에 특정 시점 이후에는 Chaotic Phase에 돌입함. (하지만, 이 내용은 PCA의 한계에 의한 것일 수 있으며, 실은 더 고차원의 평면에서 진행하고 있는 것일 수도 있음.)
• 대응되는 Learning Graph는 트리 구조였으며, 촘촘히 연결된 grid 모양을 이루고 있음.  
• 이러한 모양은 Random Seed에 영향을 받지 않았음. 다만, 이 surface는 뉴런의 개수, learning rate, batch size, normal initialization의 parameter에 연속적으로 영향을 받는 것으로 보였음. 2층 깊이와 3층 깊이 Neural Network를 비교했을 때, 마지막 두개 Layer의 Learning Graph 모양이 매우 유사한 것을 확인할 수 있음. (Figure 3, Figure5)
• Learning surface의 의미를 이해하는 방법은 Learning Surface 위에서 진행할 때의 가중치의 변화를 보는 것임. Training time과 분화하는 뉴런의 측면 전파량 각각에서 뉴런들을 샘플링하여 28x28 이미지로 가중치 벡터를 재가공하고 변화의 원인을 탐구할 수 있음. 각 training step 마다의 이미지를 관찰하면 white noise에서 출발하여 모습이 변화함을 알 수 있음. 그리고 training step을 고정하고 learning surface 위를 지나가면서 그리면 서로 다른 이미지들의 연속적인 변화를 관찰할 수 있음. 
• 마지막으로, 가운데 Hidden Layer에 대해서는 처음에는 직선 상에서 진행하다가 두개의 그룹으로 나뉘고, 각각 서로 다른 방향으로 진행함. 이 케이스는 tree와 learning surface의 중간이라고 볼 수 있음.
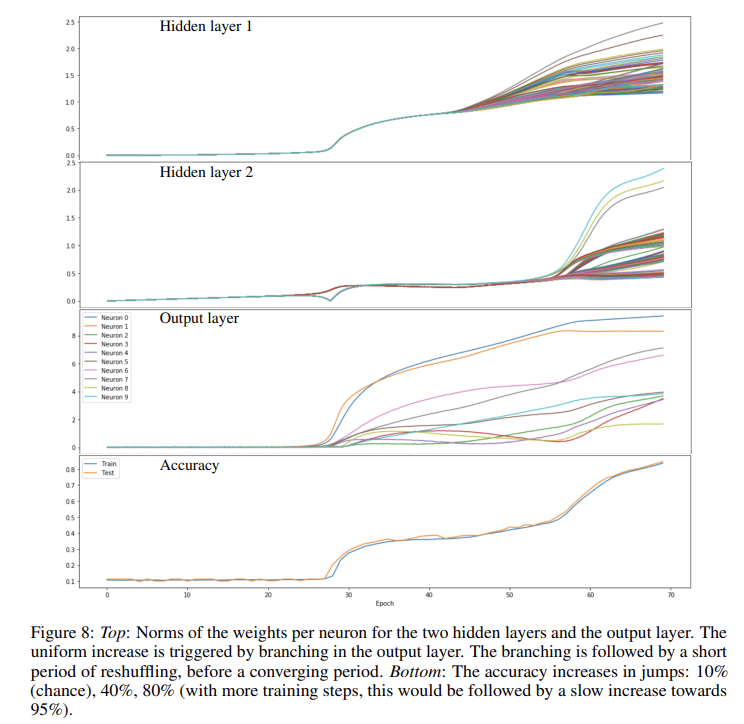
• 각기 다른 Layer의 발전 과정을 보기 위해서 가중치의 norm을 볼 수 있음. (Figure 8) Epoch이 진행됨에 따라서 2번째 은닉층의 가중치의 norm이 서서히 증가하는 것을 볼 수 있음. epoch 28 정도부터 Output Layer의 10개 뉴런으로의 분화가 진행되는데, 첫번째 은닉층의 가중치의 매우 급격한 증가와 더불어 두번째 은닉층은 두개로 분화함을 확인할 수 있음. 이 과정에서 모델 정확도가 40%까지 급증하는 것을 확인할 수 있음. epoch 45에서부터 첫번째 Hidden Layer의 가중치들이 Learning Surface 위로 분화함을 확인할 수 있고, epoch 56부터 두번째 Hidden Layer의 분화가 시작됨을 확인할 수 있음.

Discussion

• Fully Connected Feed Forward Neural Network의 학습 과정에서의 가중치들의 발전 과정을 시각화 하는 방법론을 개발함.
• 여기서 관찰한 내용에 대해서 입증할 이론적 이해가 있으면 좋을 것 같음.
• 무엇이 이러한 branching을 만드는 지에 대해서는 좀 더 연구가 필요함.
• Learning Surface의 연구도 더 필요하며, 예를 들어 Riemannian metric을 도입해 이들을 대수적인 곡선의 영역으로 옮기는 작업도 있으면 좋음.
• Initialization Schemes, Optimization Methods, Regularization, Biases, Activation Functions, 그리고 Layer의 깊이에 따른 Learning Graph들의 변화가 어떻게 되는 지 확인해야 함. 
• CNN과 RNN의 Learning Graph를 탐구하는 것도 흥미로울 것임.