Paper
- GCN : https://arxiv.org/abs/1609.02907
- GraphSAGE :https://arxiv.org/abs/1706.02216
- GAT : https://arxiv.org/pdf/1710.10903
1. 그래프 데이터 기본 개념
그래프는 노드(Vertex)와 엣지(Edge) 로 이루어지며, 이를 수학적으로 다음과 같이 표현합니다.
- 인접 행렬 (Adjacency Matrix), 노드 간 연결 관계를 나타냄.

- 노드의 특징 행렬 (Feature Matrix), 각 노드의 feature 값을 포함. (초기 Feature가 GNN을 거치면서 학습되고, 최종적으로 Embedding이 됩니다.)
2. 그래프로 표현할 수 있는 데이터 예시
- 분자 구조: 원자들이 노드, 결합이 엣지로 표현됨.
- 소셜 네트워크: 사람 간 관계를 그래프로 표현 (예: 가라테 클럽 데이터).
- 논문 인용 네트워크: 논문이 노드, 인용 관계가 엣지.
- 생물학적 네트워크: 단백질 상호작용(PPI), 유전자 네트워크.
- 추천 시스템: 사용자와 아이템의 관계를 그래프로 표현.
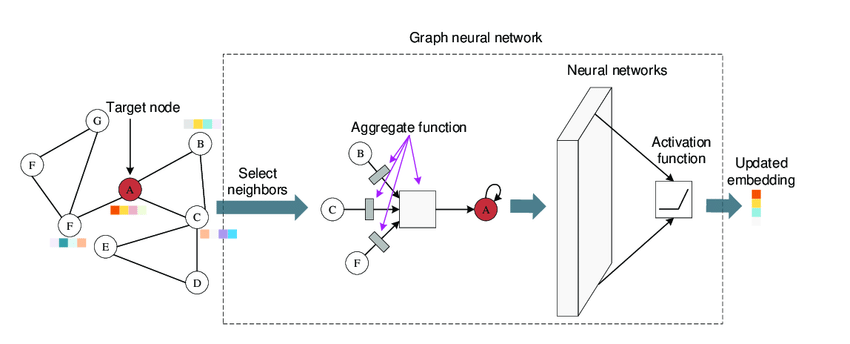
3. 일반적인 GNN의 framewor

- GNN Layer = Message + Aggregation
- GCN, GraphSAGE, GAT는 Aggregation 방식이 다름
- GCN은 평균을 사용하지만, GraphSAGE는 샘플링 후 Aggregation, GAT는 Attention 기반 Aggregation
- Activation Function을 통해 비선형성을 추가함
4. GNN의 주요 모델
- Graph Convolutional Networks (GCN, 2017)
- GraphSAGE (2017)
- Graph Attention Networks (GAT, 2018)
4-1. GCN
- GCN은 인접 행렬 A를 정규화하여 사용합니다.
- 정규화 과정: self-loop을 추가하고, 노드의 연결 개수(Degree)에 따라 정규화.
- 모든 노드가 동일한 방식으로 업데이트됨 (모든 이웃을 동일한 중요도로 반영).

4-2. GraphSAGE
- GraphSAGE는 모든 이웃을 고려하지 않고, 일부만 샘플링하여 학습.
-
- GCN은 모든 노드의 이웃을 동일한 가중치로 반영하지만, GraphSAGE는 샘플링된 이웃만 반영.
- 샘플링한 이웃끼리는 같은 W를 사용하여 독립적인 학습이 가능.즉, A의 일부 행만 샘플링하여 사용.

- Aggregation 방식을 선택할 수 있어 유연함.
- Mean Aggregation: GCN과 유사하게 이웃 노드의 평균을 계산
- LSTM Aggregation: LSTM을 이용해 이웃 정보를 순서에 따라 학습
- Pooling Aggregation: 각 이웃 노드 임베딩에 MLP를 적용 후 최대값을 선택
4-3. GAT
- GAT는 인접 행렬을 직접 사용하지 않고, Attention Score를 통해 조정된 가중치를 활용. (여기서 αij는 Softmax를 사용한 Attention 가중치)
- 즉, 단순히 인접 노드의 정보를 평균 내는 것이 아니라, 각 노드의 중요도를 학습하여 동적으로 가중치를 조정.
- 이웃 노드마다 중요도를 다르게 부여할 수 있음
- Multi-head Attention을 통해 다양한 관계를 학습 가능

5. GNN 모델 비교 요약
| GCN (Graph Convolutional Network) | 2017 | - 스펙트럴 그래프 컨볼루션을 활용 - 라플라시안 행렬을 근사하여 계산 비용 절감 |
- 전체 그래프를 필요로 하며 대규모 그래프 확장 어려움 - 이웃 노드의 중요도를 동일하게 가정 |
| GraphSAGE | 2017 | - 이웃 노드를 샘플링하여 메시지 전달 - 다양한 Aggregation 함수 (Mean, LSTM, Pooling 등) 활용 |
- 이웃 샘플링 방식에 따라 성능 차이가 존재 - 단순한 Aggregation이 구조적 정보를 충분히 반영하지 못할 수도 있음 |
| GAT (Graph Attention Network) | 2018 | - 어텐션 메커니즘을 활용하여 가중치를 학습적으로 부여 - 각 노드가 이웃 노드의 중요도를 다르게 반영 가능 |
- 그래프 크기가 커질수록 계산량 증가 - 스파스한 그래프에서의 효과적이지 않을 수도 있음 |
'Miscellaneous' 카테고리의 다른 글
| [2025-1] 박경태 - 밑바닥부터 시작하는 딥러닝 리뷰, (CH 5.2) 연쇄 법칙 (0) | 2025.03.26 |
|---|---|
| [2025-1] 임재열 - Instant Neural Graphics Primitives with a Multiresolution Hash Encoding (Instant NGP) (0) | 2025.03.22 |
| [2025-1] 박제우 - TabNet : Attentive Interpretable Tabular Learning (0) | 2025.03.15 |
| [2025-1] 임준수 - 밑바닥부터 시작하는 딥러닝 리뷰, (CH 4.2) 손실함수 (0) | 2025.03.12 |
| [2025-1] 윤선우 - 밑바닥부터 시작하는 딥러닝 리뷰, (CH 4.3) 수치 미분 (0) | 2025.03.12 |



