https://arxiv.org/abs/1511.06581
https://youtu.be/u1yYf1PCTPg?si=FfbKvYVRSnOcBJ4I
deep learning을 reinforcement learning에 접목시키려는 시도는 많았다. 여기서는 dueling network를 제안하는데, 이는 두 개의 분리된 estimator로 이루어져 있다. 하나는 state value function이고 하나는 state-dependent action advantage function이다. 이 방법은 더 나은 policy evaluation을 보여준다. 그리고 이 논문은 Atari 2600 도메인에서 SOTA를 찍었다.
기존에 RL에 쓰이는 neural network는 convolutional network, MLP, LSTM, autoencoder 등이 쓰여왔다. 이 논문에선 기존 연구들에 접목시킬 수 있는 새로운 접근 방식을 소개한다.
dueling architecture은 state value의 representation과 state-dependant action advantage를 분리한다. 이 아키텍처는 두 개의 stream으로 각각 value와 advantage function을 표현하는데, 이 두 stream은 convolutional feature learning module을 공유한다.
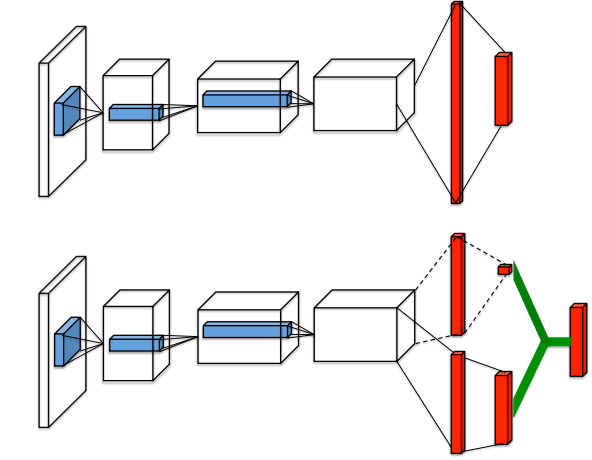
두 stream은 special aggregating layer를 거쳐 state-action value function Q를 예측한다. dueling network는 DQN, DDQN 등의 알고리즘에서 더 나은 성능을 유도한다. 또한 state value function과 advantage function을 추가적인 supervision없이 예측해낸다.
dueling architecture은 어떤 state가 가치가 있는지 좀 더 쉽게 알아낼 수 있다. 그리고 action이 별 영향을 주지 않는 state에 더 유용하다. 아래 그림은 설명을 위해 saliency map을 가져온 것으로 input video의 trained value와 advantage stream의 jacobian을 계산하여 value와 advantage saliency map을 나타낸 것이다.

그림의 위와 아래는 각각 다른 timestep에서 saliency map을 가져온 것이다. 첫번째 timestep에서, value network stream은 길에 집중하고, 점수에도 집중한다. advantage stream은 어디에도 집중하지 않는데 어떤 action을 하던 별 영향이 없기 때문이다. 그러나 두번째 timestep에선 advantage stream은 앞의 차에 집중한다. action이 중요한 상황이기 때문이다.
dueling architecture은 더 빠르게 옳은 action을 찾아감이 실험으로 확인되었다.
$s_t = (x_{t - M + 1}, \ldots, x_t) \in S$ (M개의 이미지 프레임으로 이루어진 상태 $s_t$)
$a_t \in A = \{1, \ldots, |A|\}$ : discrete action set에서 action 고르기
$r_t$: reward signal
우리는 이제 advantage function을 아래와 같이 정의한다.
$ A^\pi(s, a) = Q^\pi(s, a) - V^\pi(s) $
이 때 $ \mathbb{E}_{a \sim \pi(s)}\big[A^\pi(s, a)\big] = 0 $ 이 성립한다.
단순히 state와 action을 받아서 Q함수를 예측하는 것보다, state가 얼마나 좋은지 예측하는 V와 action의 상대적인 중요성(state에 따라) A를 이용하면 더 좋은 결과를 얻을 수 있다.
dueling network에서 윗쪽 stream의 FC layer의 output을 scalar $ V(s; \theta, \beta) $라 하고 아래 stream의 output을 $|A|$차원 벡터 $ A(s, a; \theta, \alpha) $라 하자. 여기서 $ \theta $는 convolution layer의 파라미터들, $ \alpha , \beta $는 두 stream의 FC layer의 파라미터들이다.
aggregating module을 아래와 같이 쓸 수 있다.
$ Q(s, a; \theta, \alpha, \beta) = V(s; \theta, \beta) + A(s, a; \theta, \alpha) $
하지만 이렇게 하면 $ V(s; \theta, \beta) $가 state-value function의 좋은 estimator인지,
$ A(s, a; \theta, \alpha) $ 가 좋은 advantace function estimator인지 알 수 없다.
이를 해결하기 위해 먼저 deterministic policy의 경우를 생각하면
$a^* = \arg\max_{a' \in A} Q(s, a')$
$Q(s, a^*) = V(s)$
$A(s, a^*) = 0$에서
$ Q(s, a; \theta, \alpha, \beta) = V(s; \theta, \beta) + A(s, a; \theta, \alpha) - \max_{a' \in |\mathcal{A}|} A(s, a'; \theta, \alpha) $가 된다.
여기서 $ a^* = \arg\max_{a' \in A} Q(s, a'; \theta, \alpha, \beta) = \arg\max_{a' \in A} A(s, a'; \theta, \alpha) $이고
$ Q(s, a^*; \theta, \alpha, \beta) = V(s; \theta, \beta) $
이렇게하면 state value function와 advantage function을 예측할 수 있다.
다른 방법은 아래와 같다.
$ Q(s, a; \theta, \alpha, \beta) = V(s; \theta, \beta) + A(s, a; \theta, \alpha) - \frac{1}{|A|} \sum_{a'} A(s, a'; \theta, \alpha) $
이 논문의 실험에선 이 마지막 방법을 썼다.
이 논문의 실험에선 dueling network를 DQN, DDQN, prioritized replay 등등에 적용시켜 성능이 향상됨을 보였다.
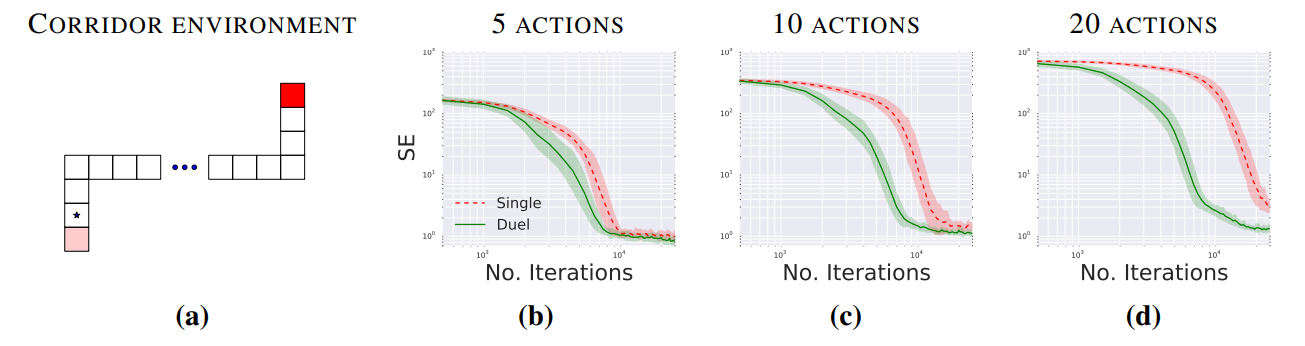
위 그림에선 dueling network가 single보다 더 학습이 빠르고, 특히 action이 다양할 수록 효과는 커짐을 보여준다.

위 표에선 duel network를 쓸 때의 성능 향상을 보여준다.
이 논문에선 state value에 더 많은 resource를 할당해 예측함으로서, 더 정확한 temporal difference-based 방법론의 적용을 할 수 있었다고 설명한다.
'Miscellaneous' 카테고리의 다른 글
| [2025-1] 김지원 - Efficiently Modeling Long Sequences with Structured State Spaces (0) | 2025.01.25 |
|---|---|
| [2025-1] 계진혁 - Policy-based objectives (0) | 2025.01.24 |
| [2025-1] 김학선 - Policy Gradient (0) | 2025.01.20 |
| [2025-1] 노하림 - PER: Prioritized Experience Replay (0) | 2025.01.19 |
| [2025-1] 정지우 - Q-learning (심화편) [혁펜하임 강화학습 4-2강 정리] (0) | 2025.01.12 |



