[2025-2] 최민서 - Direct Preference Optimization:Your Language Model is Secretly a Reward Model

[논문링크] https://arxiv.org/abs/2305.18290

Direct Preference Optimization: Your Language Model is Secretly a Reward Model

 

1. Introduction

 

Large unspervised language model(LM)은 굉장히 광범위하게 사용되는 언어 모델이다. 현실에서는 LM이 특정한 기능을 하도록 따로 파인튜닝을 해 주어야 하는데, 이 때 주로 사용되는 방법이 강화학습(Reinforcement Learning, RL)이다. 특히 LM이 생성한 두 텍스트 중 연구자(혹은 사용자)가 더 선호하는 것을 골라 이러한 경향성을 다시 학습시키는 preference learning의 분야에서 강화학습을 이용하는 방법론(Reinforcement Learning from Human Feedback, RLHF)은 가장 좋은 성과를 보이고 있다. 현재까지 연구된 RLHF 방식은 아래의 두 단계로 구성된다.

 

1)선호 경향성을 reward model에게 학습시킨다.

2) 학습된 reward model을 바탕으로 RL을 수행하여 LM을 파인튜닝한다.

 

하지만 이러한 RLHF 파이프라인은 컴퓨팅 자원을 굉장히 많이 필요로 한다. 전체 파인튜닝 과정이 reward model의 학습과 LM 파인튜닝의 두 부분으로 나누어져 있어 비효율적이다. 또한 RL 알고리즘 수행 과정에서 LM이 텍스트를 생성하고, 이것의 reward를 계산 및 backpropagation을 여러번 진행하는 과정에서 컴퓨팅 자원이 많이 소모된다. 

 

본 논문에서는 Direct Preference Optimization(DPO) 알고리즘을 제시하여 이러한 문제를 해결한다. DPO는 reward model의 학습 및 LM의 파인튜닝을, 단일 목적함수에 대한 최적화 문제로 바꾼다. 해당 목적함수는 명시적으로 reward model에 대한 정보를 담고 있지 않고, 다만 정책(LM)의 모델링에 대해서만 표현된다. 즉 DPO에서는 정책으로 표현되는 단일 목적함수를 최적화함으로써, reward model의 학습 및 LM의 파인튜닝을 동시에 수행한다.

 

2. Preliminaries

 

선행연구에서 RLHF 파이프라인은 아래의 세 단계로 구성된다.

 

1)Supervised Fine-tuning (SFT) : LM을 사용자가 원하는 방식으로 파인튜닝

2) Preference Sampling and Reward Learning : 선호 데이터 쌍 추출 후 reward model 학습

3) RL optimization : 학습된 reward model 이용하여 강화학습 수행

SFT

RLHF 파이프라인은 비지도학습 방식으로 학습된 LM을 사용자가 원하는 방식으로 파인튜닝하면서 시작된다. 파인튜닝된 모델을 $\pi^{\matrhm{SFT}$라 한다.

 

Reward Modelling Phase

학습된 SFT 모델을 이용하여 프롬프트 $x$에 대응되는 출력 쌍 $(y_1,y_2)$를 준비한다. 이후 인간(사용자나 전문가 등)이 직접 라벨을 평가해 $y_w > y_l \, | \, x$를 라벨링한다. 이러한 인간의 선호도를 완벽하게 reward로 반영하는 가상의 reward model을 $r^*(x,y)$라 한다. 선호도를 모델링하는 방법에는 여러가지가 있는데 그 중 Bradley-Terry(BT) 모델은 아래와 같이 모델링한다.

 

$$p^{*} (y_1 > y_2  \, | \, x) = \frac{\exp (r^*(x,y_1)) }{\exp(r^*(x,y_1)) + \exp(r^*(x,y_2))} $$

 

$p^*$는 인간 선호도의 확률분포를 나타낸다. $p^*$로부터 샘플링한 데이터셋 $\mathcal{D} = \{ x^{(i)}, y_w^{(i)}, y_l^{(i)} \}$이 있을 때, reward model을 $r_\phi(x,y)$로 모델링하여 maximum likelihood를 통해 학습시킬 수 있다. 이 때 negative log-likelhood 손실함수는 아래와 같이 나타난다.

 

$$ \mathcal{L}_R (r_\phi, \mathcal{D}) = - \mathbb{E}_{(x,y_w,y_l)\sim\mathcal{D}} \left[ \log \sigma(r_\phi(x,y_w) - r_\phi(x,y_l)) \right]$$

 

위 수식에서 $\sigma$는 로지스틱 함수를 나타낸다. 선행 연구에서는 reward function이 낮은 분산을 갖도록 reward를 정규화해주었다. 즉 모든 $x$에 대하여 $\mathbb{E}_{x,y\sim\mathcal{D}}[r_\phi(x,y)]=0$가 되도록 설정해주었다.

 

RL Fine-Tuning Phase

RL  파인튜닝 단계에서는 학습된 reward model을 통해 LM을 파인튜닝한다. 최적화 목적함수는 아래와 같이 나타난다.

 

$$ \max_{\pi_\theta} \mathbb{E}_{x\sim\mathcal{D},y\sim\pi_\theta(y|x)} [r_\phi(x,y)] -\beta D_{KL}\left[ \pi_\theta(y|x) || \pi_{ref}(y|x) \right] $$

 

즉 주어진 데이터셋에 대하여 reward를 최대화하는 정책 $pi_\theta$를 찾되, 기존 정책인 $\pi_{\mathrm{ref}}$로부터 정책이 너무 멀어지지 않도록 해야한다. $\beta$는 $\pi_{\mathrm{ref}}$로부터 허용되는 변화의 정도를 나타내는 하이퍼파라미터이다. 목적함수의 KL항은 학습 중 정책 모델이 베이스 모델로부터 너무 멀어지지 않도록 유지하고, 동시에 생성되는 결과물의 다양성을 유지하고 모드 붕괴를 막아준다.

 

LM의 경우, 위 목적함수는 일반적으로 미분이 불가능하기 때문에, 강화학습을 통해 학습을 진행한다. 표준적인 접근법은 reward function $r(x,y) = r_\phi(x,y) - \beta(\log\pi_\theta(y|x) - \log \pi_{ref}(y|x))$을 사용하고 PPO 알고리즘을 이용하여 목적함수를 최대화한다.

 

3. Direct Preference Optimization

 

기존의 RLHF 방법론은 앞서 설명한 절차를 따른다. 본 논문에서는 적절한 reward model parameterization을 특정하여 단순한 목적함수를 통하여 동일한 최적화 결과를 얻을 수 있도록 한다. 이를 위해 reward function을 optimal policy로 변환하여 reward model의 최적화 없이 policy의 최적화만으로 원하는 결과를 얻을 수 있도록 한다. 이러한 논문의 방법론을 Direct Preference Optimization(DPO)라 명명한다.

 

Deriving the DPO objective

Section 2에서 보았던 KL-constrained 목적함수의 최적해는 아래와 같이 나타난다.

 

$$\pi_r(y|x) = \frac{1}{Z(x)} \pi_{ref}(y|x) \exp (\frac{1}{\beta}r(x,y))  $$

 

이에 대한 증명은 논문의 Appendix A.1에 나와있다.

위 수식에서 $Z(x)=\sum_y \pi_{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))$는 정규화 함수이며, 최적해 $\pi_r(y|x)$는 사용한 reward function $r$의 종류에 따라 달라진다.

만약 기존의 RLHF에서 그랬듯이, 따로 학습한 reward function $r_\phi$를 갖고 있더라도, 위 수식에 따라 최적 정책 $\pi_r(y|x)$를 계산하는 것은 불가능하다. 정규화항 $Z(x)$를 계산할 수 없기 때문이다.

 

위 수식을 reward function $r(x,y)$에 대하여 정리하면 아래와 같이 나온다.

 

$$ r(x,y) = \beta \log \frac{\pi_r(y|x)}{\pi_{ref}(y|x)} + \beta \log Z(x) $$

 

이와 같은 reparameterization을 ground-truth reward $r^*$와 이에 대응되는 최적 정책 모델 $\pi^*$에 적용할 수 있다. 이를 section2에서 보았던 BT 프레임워크의 preference model에 대입하면 아래와 같이 나온다.

 

$$ p^* (y_1>y_2\,|\,x) = \frac{1}{1+\exp \left(  \beta \log \frac{\pi^*(y_2|x)}{\pi_{ref}(y_2|x)} - \beta \log \frac{\pi^*(y_1|x)}{\pi_{ref}(y_1|x)}    \right)} $$

 

이에 대한 증명은 논문의 Appendix A.2에 나와있다. BT 모델 대신 Placket-Luce 모델을 사용해도 유사한 결과를 얻을 수 있고 이는 논문의 Appendix A.3에 나와있다.

 

이제 section2에서 봤던 목적함수를 reward model 대신 policy model 만을 이용해서 표현할 수 있다. NLL을 최소화하도록 손실함수를 아래와 같이 설정할 수 있다.

 

$$ \mathcal{L}_{\mathrm{DPO}} (\pi_\theta ; \pi_{ref}) = - \mathbb{E}_{(x,y_w,y_l)\sim \mathcal{D}} \left[ \log \sigma \left(  \beta \log \frac{\pi_\theta(y_w|x)}{\pi_{ref}(y_w|x)} - \beta \log \frac{\pi_\theta(y_l|x)}{\pi_{ref}(y_l|x)}    \right) \right] $$

 

이를 통해 reward model의 명시적 최적화 없이도 $\pi_\theta$에 대응되는 reward model을 최적화할 수 있다.

 

What does the DPO update do?

DPO의 작동원리를 이용하기 위해 $ \nabla_\theta \mathcal{L}_{\mathrm{DPO}} $를 분석할 수 있다.

 

$$ \nabla_\theta \mathcal{L}_{\mathrm{DPO}}(\pi_\theta ; \pi_{ref}) = -\beta \mathbb{E}_{(x,y_w,y_l)\sim \mathcal{D}} \left[  \sigma(\hat{r}_\theta(x,y_l) - \hat{r}_\theta(x,y_w)) \left[ \nabla_\theta \log \pi(y_w|x) - \nabla_\theta \log \pi(y_l|x)   \right] \right] $$

 

위 수식에서 $\hat{r}_\theta(x,y)=\beta\log\frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)}$는 $\pi_\theta$에 대응되는 implicit reward function이다. $ \sigma(\hat{r}_\theta(x,y_l) - \hat{r}_\theta(x,y_w)) $는 reward 예측값이 잘못됐을 때 큰 값을 가지는 스칼라 값이다. 즉 implicit reward model의 예측값이 크게 잘못됐을 때 gradient update의 크기가 커진다. $ \nabla_\theta \log \pi(y_w|x)$는 $y_w$의 likelihood의 증가를 나타내는 벡터이고 $\nabla_\theta \log \pi(y_l|x) $은 $y_l$의 증가를 나타내는 벡터이다. 

 

즉 $\mathcal{L}_{\mathrm{DPO}} $는 $ \pi(y_w|x) $의 확률이 증가하고 $\pi(y_l|x)$의 확률이 감소하는 방향으로 업데이트되고,  implicit reward model의 예측값이 잘못될수록 크게 업데이트된다.

 

DPO outline

표준적인 DPO 파이프라인은 아래와 같이 구성된다.

 

1) $\pi_{ref}(\dot | x)$로부터 $y_1,y_2$를 샘플링한 후 선호하는 데이터를 골라 라벨링하여 데이터셋 $\mathcal{D}=\{ x^{(i)}, y_w^{(i)},y_l^{(i)} \}_{i=1}^N$을 구성한다.

2) 적절한 $\beta$ 값을 설정한 후, $\mathcal{L}_{\mathrm{DPO}}$를 최소화하여 LM $\pi_\theta$를 최적화한다. $\pi_{ref}$는 $\pi^{\mathrm{SFT}}$로 최적화한다.

 

참고(논문의 내용이 아닌 이해를 돕기 위해 추가된 내용)

 

DPO와 기존의 RLHF 방식을 비교했을 때, 아래와 같이 정리할 수 있다.

 

- RLHF

1) $p^{*} (y_1 > y_2  \, | \, x) $가 최대화되도록 $r_\phi$ 학습

2) 학습된 reward model 이용하여 $\mathbb{E}_{x\sim\mathcal{D},y\sim\pi_\theta(y|x)} [r_\phi(x,y)] -\beta D_{KL}\left[ \pi_\theta(y|x) || \pi_{ref}(y|x) \right] $가 최대화되도록 $pi_\theta$ 학습

 

- DPO

1) $\pi_\theta(y|x) = \frac{1}{Z(x)} \pi_{ref}(y|x) \exp (\frac{1}{\beta}r_\phi(x,y))  $가 $ \max_{\pi_\theta} \mathbb{E}_{x\sim\mathcal{D},y\sim\pi_\theta(y|x)} [r_\phi(x,y)] -\beta D_{KL}\left[ \pi_\theta(y|x) || \pi_{ref}(y|x) \right] $의 최적해임을 이용해서 모델링한 $\pi_\theta$에 대응되는 implicit reward function $r_\phi(x,y)$ 정의

2) $p^{*} (y_1 > y_2  \, | \, x)$가 최대화되도록 $\pi_\theta$ 학습

 

DPO는 RLHF와 다른 목적함수를 최대화하고 이 때문에 두 알고리즘은 다른 최적해를 갖는 것처럼 보인다. 하지만 DPO 알고리즘을 자세히 보면, 2번 과정에서 $\pi_\theta$를 학습시키면, 동시에 대응되는 $r_\phi$가 학습되는 것과 같은 효과를 같고 (reparameterization에 의해), 학습된 $\pi_\theta$는 RLHF 2번의 목적함수의 해석적 최적해이기 때문에 두 알고리즘의 최적해는 같다고 할 수 있다.

 

4. Theoretical Analysis of DPO

 

4.1 Your Language Model is Secretely a Reward Model

 

본 섹션에서는 DPO 알고리즘에서 수행한 reparameterization과 관련된 수학적 분석을 진행한다. 먼저 아래와 같이 reward function의 equivalence를 정의한다.

 

 

위의 정의는 equivalence relation의 수학적 정의를 만족함을 쉽게 확인할 수 있으므로, reward function들을 equivalence class로 나눌 수 있다. 또한 reward function의 equivalence class에 관한 아래의 lemma들을 주장할 수 있다.

 

 

이에 대한 증명은 논문의 Appendix A.5에 나와있다.

 

즉 위의 lemma들에 따르면, 같은 equivalence class에 속하는 reward function들은 같은 preference distribution 및 optimal policy를 갖고, DPO 알고리즘의 관점에서 이들을 구별할 수 없다. 이를 이용하여 아래의 theorem을 증명할 수 있다.

 

 

이에 대한 증명은 논문의 Appendix A.6에 나와있다.

 

DPO 목적함수 유도 과정에서 볼 수 있듯이, reward model로부터 대응되는 policy model이 계산되는 구조이기 때문에, 어떤 policy model이 주어졌을 때, 이에 대응되는 reward model이 존재하느냐? 라는 의문이 생길 수 있다. 하지만 위 theorem에 따르면 각 reward class마다 대응되는 policy model이 존재한다. 즉 DPO의 최적해와 RLHF의 최적해가 같다는 것을 보다 엄밀하게 논증할 수 있다.

 

또한 위 theorem에 의해, 우리는 policy model에 대응되는 reward classd의 reward function들 중 하나를 아래와 같이 특정할 수 있다.

 

$$  r(x,y) = \beta\log\frac{\pi(y|x)}{\pi_{ref}(y|x)} $$

 

앞서 section 3에서 봤던 reparameterization 수식과 비교할 때, 위 reward function은 정규화항 $\beta \log Z(x)$가 $0$이므로 아래와 같은 제약조건을 만족한다고 볼 수 있다.

 

$$ \sum_y \pi_{ref}(y|x) \exp(\frac{1}{\beta}r(x,y)) = 1 $$

 

정리하면, 기존의 RLHF 방법에서는 reward model을 LL을 최대화하는 방식으로 학습시키는데, 이 때 같은 class의 reward function은 같은 preference distribution을 가지므로 최적화의 관점에서 구분할 수 없다. 즉 최적의 reward model에 대해 해석적으로 접근하기 위해서는 특정한 제약조건을 걸어 reward class의 함수들 중 하나의 reward function을 특정해 주어야 한다. DPO에서는 이러한 제약이 위 수식을 통해서 진행되며, 위 수식에 따라 최적의 reward function은 $  r(x,y) = \beta\log\frac{\pi(y|x)}{\pi_{ref}(y|x)} $로 자연스럽게 정의된다.

 

4.2 Instability of Actor-Critic Algorithms

 

DPO 프레임워크를 통해, RLHF를 위한 표준적인 actor-critic 알고리즘의 불안정성을 설명할 수 있다. $\pi^*$를 최적 정책이라 하고, $D_{\mathrm{KL}}[\pi_\theta(y|x) || \pi^*(y|x)]$를 최소화한다고 할 때, 목적함수는 아래와 같이 나타난다.

 

$$ \max_{\pi_\theta} \mathbb{E}_{\pi_\theta(y|x)} \left[ r_\phi(x,y) - \beta\log \sum_y \pi_{ref}(y|x)\exp(\frac{1}{\beta} r_\phi(x,y) ) - \beta\log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)} \right] $$

 

이 때 $r_\phi(x,y)$는 DPO 수식에 따라 정의된 $\pi^*$에 대응되는 reward model이다. $ \beta\log \sum_y \pi_{ref}(y|x)\exp(\frac{1}{\beta} r_\phi(x,y) )  $는 정규화항으로 gradient의 분산을 줄이는 역할을 하며 최적해에는 영향을 주지 않는다. 정규화항을 계산하는 것은 쉽지 않은데, actor-critic 알고리즘 관련 선행연구에서는 인간이 직접 만든 최적 베이스라인을 사용하므로, 정규화항에 대한 단일 샘플 Monte-Carlo estimate이라 볼 수 있다. 따라서 추정이 불안정할 수밖에 없다. DPO에서는 베이스라인과 관련된 연산을 하지 않기 때문에, 이런 일이 일어나지 않는다.

 

5. Experiments

 

논문의 본 섹션에서는 앞에서 이론적으로 확인했던 내용을 실험으로 검증한다. DPO를 이용하여 SFT를 파인튜닝 했을 때, 기존의 RLHF 방법론보다 높은 reward를 갖는 데이터를 생성하면서, 베이스 모델로부터 거리가 멀지 않음을 확인한다.

 

Tasks

세 개의 text generation task를 수행한다. 모든 실험에서 알고리즘은 preference dataset $\mathcal{D}=\{x^{(i)},y_w^{(i)},y_l^{(i)}\}_{i=1}^N$에서 정책을 학습시킨다.

 

Task1) Controlled Sentiment Generation

$x$는 IMDB 데이터셋의 영화리뷰의 서문이고 정책 모델은 positive sentiment의 리뷰 $y$를 생성해야 한다. SFT는 GPT-2-large를 IMDB 데이터셋으로 파인튜닝하여 만든다. 그 후 SFT로 텍스트들을 생성한 후 pre-trained sentiment classifier를 optimal reward model로 사용하여 $p(\mathrm{positive}|x,y_w)>p(\mathrm{positive}|s,y_l)$이 되도록 데이터를 라벨링하여 preference dataset $\mathcal{D}$를 만든다.

 

Task2) Summarization

$x$는 Reddit의 forum post이고 정책 모델은 post의 main point를 반영하여 이를 요약한 summary $y$를 생성해야 한다. Reddit TL;DR summarization dataset을 사용한다. SFT는 GPT-J-6B를 summarization dataset으로 파인튜닝하여 만든다. 그 후 Stiennon et al.에서 모은 human preferences를 이용하여 preference dataset $\mathcal{D}$를 준비한다.

 

Task3) Single-turn Dialogue

$x$는 인간이 하는 다양한 분야의 질문이고 정책 모델은 이에 대한 적절한 답변 $y$를 생성해야 한다. Anthropic Helpful and harmless dialgoue dataset을 이용하는데 데이터셋에는 LLM이 생성한 답변 쌍과 인간이 선호하는 답변이 라벨링되어 있다. 해당 데이터셋을 preference dataset $\mathcal{D}$로 구성한다. 또한 해당 태스크에는 사용할만한 SFT 모델이 없기 때문에 데이터셋에서 인간이 선호하는 답변들만 골라 Pythia-2.8B를 파인튜닝한다.

 

Evaluation

각 태스크별로 다른 평가 방식을 적용한다.

 

Task1에서는 ground truth reward function(pre-trained sentiment classifier)에 접근 가능하므로, 알고리즘으로 학습한 모델이 생성한 텍스트의 reward와 모델과 베이스 모델의 KL divergence를 frontier를 비교하는 방식으로 평가한다.

 

Task2,3에서는 ground truth reward function에 접근 불가능하므로 frontier를 비교하는 방법은 불가능하다. 대신 GPT-4를 ground truth의 proxy라 상정하고 baseline policy와 비교하여 각 알고리즘의 win rate을 평가한다. Task2의 경우, test set의 reference summary를 베이스라인으로 보고, Task3의 경우, test set의 선호되는 응답을 베이스라인으로 보았다.

 

Methods

실험에서는 DPO와 다른 모델 및 알고리즘들을 비교한다. 아래는 비교대상이 되는 모델들이다.

1) zero-shot prompting with GPT-J => Task2

2) 2-shot prompting with Pythia-2.8B => Task3

3) SFT model => Task1,2,3

4) Prefered-FT(Finetunes SFT(or LM) with $\{y_l\}$ => Task1,2,3

5) Unlikelihood(Optimizes policy to maximize $p(y_w)$ and minimize $p(y_l)$ => Task 1

6) PPO => Task1,2,3

7) PPO-GT(Uses ground truth reward) => Task1

8) Best of N(Sample N from SFT and chooses one with highest reward) => Task1,2,3

 

5.1 How well can DPO optimize the RLHF objective?

 

RLHF 알고리즘의 성능을 비교할 때는 모델의 성능(높은 reward)뿐만 아니라 베이스라인 정책 모델로부터 얼마나 멀어졌는지도 봐야한다. 위에서 제시한 세 개의 task에 대해서 각 모델의 성능을 아래에서 비교하였다.

 

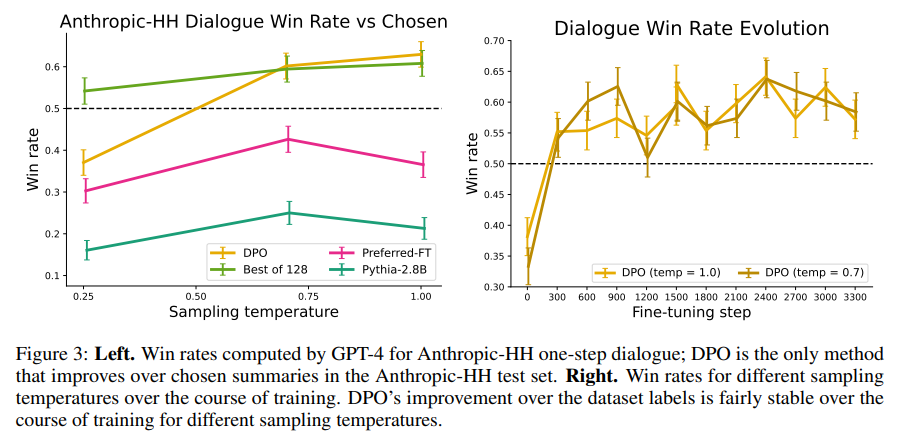
Figure2의 left에서 확인할 수 있듯이, task1에서 DPO는 다른 알고리즘 및 모델과 비교했을 때 월등한 성능을 보였다. 특히 PPO와 비교했을 때 더 좋은 성능을 보였으며, 이를 통해 아래의 사실들을 확인할 수 있었다.

 

• DPO와 PPO는 같은 목적함수를 최적화하지만 DPO가 더 효율적이다.
• Task1의 경우(ground truth reward에 접근 가능한 경우)에도 DPO가 PPO보다 효율적이다.

 

5.2 Can DPO scale to real preference datasets?

 

Task1에서 DPO가 더 잘 작동하는건 확인했으니, 이제 실제 human preference dataset을 사용한 경우에도 DPO 알고리즘이 이를 잘 반영하여 학습했는지 task2,3의 결과를 통해 확인한다.

 

Task2의 경우, 각 모델이 생성한 summarization과 test dataset의 summarization reference 중 GPT-4가 판단하기에 더 인간이 선호할만한 답변을 고르고 이에 대한 win rate를 기록하였다. 결과는 Figure2의 right에서 확인할 수 있다. 모든 sampling temperature에서 DPO가 다른 알고리즘 대비 월등한 성능을 보임을 확인할 수 있었다. 이는 DPO의 하이퍼파라미터 $\beta$를 주의깊게 파인튜닝하지는 않은 결과로, 더 좋은 성능을 기대할 수 있다. 또한 DPO가 PPO보다 temperature 변화에 견고함을 확인할 수 있었다.

 

Task3의 경우, 결과는 Figure3에서 확인할 수 있다. 마찬가지로 GPT-4를 이용하여 win rate를 기록하였으며 대부분의 temperature에서 DPO가 좋은 성능을 보였다. 또한 task3의 well-known source의 방식으로 PPO 파인튜닝을 해보았지만 모든 경우에 Pythia-2.8B보다 열등한 성능을 보였다. 반면 DPO는  Best-of-128과 비교했을 때도 크게 밀리지 않았는데, 이는 계산량이 128배 더 작다는걸 고려하면 꽤나 고무적인 결과이다. Figure3의 right에서 DPO는 비교적 빨리 수렴하는 것도 확인할 수 있었다. 

 

5.3 Generalization to a new input distribution

 

PPO와 DPO 알고리즘이 distribution shift 하에서 얼마나 좋은 성능을 내는지 비교하기 위해 task2에서 학습한 Reddit summarization 모델이 CNN/DailyMail dataset의 news article에 대해서도 잘 동작하는지 비교한다. 결과는 아래와 같고 DPO가 PPO보다 좋은 성능을 가짐을 확인할 수 있다.

 

 

5.4 Validating GPT-4 judgments with human judgments

 

Task2,3에서 ground truth reward model에 대한 proxy로 GPT-4를 이용하였다. 해당 태스크에서 GPT-4가 타당함은 이미 선행 연구에서 증명되었지만, 본 논문의 실험 환경에서 GPT-4를 이용한 선호도 평가가 인간의 선호도 평가와 얼마나 유사한지 실험적으로 확인한다.

 

GPT-4(S)는 simple prompt를 이용한 평가이고 GPT-4(C)는 concise prompt를 이용한 평가이다. Task2의 세팅에서 실험했고 각 모델을 test dataset summarization baseline과 비교했다. 실험결과는 아래와 같다. 표에서 확인할 수 있듯이, 사람들끼리 의견이 일치된 정도보다 사람과 GPT-4가 일치한 정도가 비슷하거나 더 많다는 것을 확인할 수 있었다. 

 

6. Discussion

 

DPO는 LM의 RLHF 태스크에서 기존의 연구와 같은 목적함수를 최적화하면서, 강화학습보다 훨씬 간단한 방법으로 human preference를 단일 목적함수로 직접 학습하는 알고리즘이다. 단순히 구현이 쉽고 간단할뿐만 아니라 여러 태스크에서 기존의 모델보다 성능이 뛰어남이 검증되었다.

 

논문에서는 아래와 같은 한계 및 연구과제를 제시한다.

 

• Out of distribution 상황에서도 DPO가 좋은 성능을 보임을 간단한 테스트를 통해 확인했지만, 일반적인 결론을 말하려면 더 연구가 필요하다.
• PPO의 unlabled prompt 활용을 DPO에도 적용할 수 있는가?
• Reward over-optimization(reward model을 너무 최대로 최적화하면 인간이 보기에 오히려 이상해지는 현상)이 DPO에서도 나타날 수 있는가?
• 논문에서는 최대 6B 파라미터 수준에서만 실험을 했는데 훨씬 규모가 큰 LLM에서도 잘 적용되는가?
• GPT-4를 이용한 평가에서 프롬프트를 어떻게 쓰느냐에 따라 평가가 꽤 달라지기 때문에 이와 관련된 일반적인 연구가 필요하다.
• 논문에서는 텍스트 LM에서만 DPO를 적용했지만, 이미지, 오디오, RL 환경 등 다른 generative 모델로의 확장