https://arxiv.org/abs/1609.02907
Semi-Supervised Classification with Graph Convolutional Networks
We present a scalable approach for semi-supervised learning on graph-structured data that is based on an efficient variant of convolutional neural networks which operate directly on graphs. We motivate the choice of our convolutional architecture via a loc
arxiv.org
1. Introduction
- 본 연구에서 핵심이 되는 주제는 Label이 일부에만 적용되어 있는 상황에서 그래프 구조의 데이터를 다루는 문제를 논의한다. 여기서는 이 task를 graph based semi supervised learning이라고 한다.
- 기존 그래프 기반의 정규화 목적 함수는 다음과 같다

- 여기서 L0은 레이블링이 되어있는 부분에서 지도학습 손실을 나타내고 Xi는 노드 특성 벡터로 구성된 행렬이다. 델타는 Unnormalized graph Laplacian을 나타내는데, 이 그래프는 G = (V, E)에 의해 정의된다.
- 이 식은 그래프에서 서로 연결된 노드들은 같은 레이블을 가질 가능성이 높다는 가정에서 출발한다.
- 그러나 이 가정은 모델링 용량을 제한할 수 있는데, 엣지가 반드시 노드 간의 유사성을 나타내는것은 아니고 추가적인 정보를 담고 있을 수 있기 때문이다.
- 따라서 본 연구는 이러한 복잡한 정규화 없이도 그래프 구조를 활용할 수 있도록 하는 방식인 GCN을 제안한다.
- 그래프 구조 A와 노드 특징 X를 직접 신경망의 입력으로 넣고 학습한다 : f(X, A)
- 이를 통해 그래디언트가 그래프를 따라 흘러가도록 만들어, Unlabeled Data를 학습할 수 있게 함.
2. Fast Approximate Convolutions on Graphs
- 다음은 이어지는 GCN 모델에서 따르는 layer wise propagation rule이다
- 즉, 한 노드가 있을 때, 자기 자신과 연결된 이웃들을 본 후, 그 이웃들이 가지고 있는 정보를 평균내서 가중치를 곱하고 비선형 변환을 통해 다음 단계의 노드 표현을 만드는 것이다.


- 이를 위해 Chebyshev 다항식 근사를 고려할 수 있다. 이 공식은 Hammond의 2011년 연구에서 자세히 서술되어 있다.
- 간단히 요약하자면 고유값 분해 없이 필터를 L이라는 행렬에 대해 근사한다는 뜻이다.
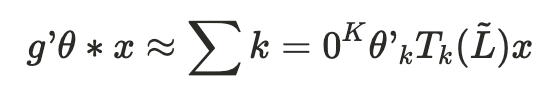
💡
푸리에 변환
: 신호를 주파수 성분으로 바꿔주는것, 여기서 그래프 푸리에 변환이란 라플라시안 고유벡터를 기저로 사용해서 변환
라플라시안 행렬
: 그래프 연결 구조를 표현하는 행렬
2.1 Spectral Graph Convolutions
- Convolution을 진행하려면 grid 형태가 필요한데, 그래프 구조는 그렇지 않기 때문에 직접 필터링이 어렵다.
- 이러한 문제를 위해 라플라시안 행렬을 이용한 그래프 푸리에 변환을 시도할 수 있으나 이는 계산복잡도가 $O(N^2)$으로 비효율적이라는 점이 한계로 지적되었다.

- x : 그래프 위의 신호 (각 노드 값)
- U^t x : 신호를 그래프 푸리에 변환
- g_theta : 필터
- UgU^tx : 다시 신호 도메인으로 복원
- 이를 위해 Chebyshev 다항식 근사를 고려할 수 있다. 이 공식은 Hammond의 2011년 연구에서 자세히 서술되어 있다.
- 간단히 요약하자면 고유값 분해 없이 필터를 L이라는 행렬에 대해 근사한다는 뜻이다.

2.2 Layer Wise Linear Model
- 이 신경망 모델은 위와 같은 수식과 point wise 비선형 함수를 중첩해서 쌓는다.
- 여기서 K=1로 제한한다. 즉 Chebyshev 다항식을 1차까지만 쓴다는 뜻인데, 그렇게 되면 단순한 선형 필터가 된다. (Kipf&Welling의 단순화)
- 비록 한 층에는 이렇게 쓰더라도 여러 층을 쌓으면 복잡하고 표현력 있는 Convolutional Filter를 사용할 수 있는데, 이를 통해 오버피팅을 피하거나 더 깊은 모델을 만들 수 있는 장점을 갖는다. 노드 차수가 매우 복잡한 경우에 적절히 쓰일 수 있다.
- 그래프 라플라시안의 최대 고유값은 원래 계산이 복잡하지만 본 연구에서는 람다의 최대를 2로 가정한다.
- 여기서 세타0과 세타1은 Learnable Parameter이다. 이 필터 파라미터는 그래프 전체에 걸쳐서 공유된다.

- 이러한 필터를 연속적으로 적용하게 되면 결과적으로 노드의 k차 이웃에 대해 합성곱을 수행하는 효과가 있다. 또한 오버피팅 방지 및 연산 효율을 위해 파라미터 수를 제한하는 것이 더 유리하다.
- 이 연구에서는 따라서 2개의 학습 가능한 파라미터 0과 1을 합쳤다.
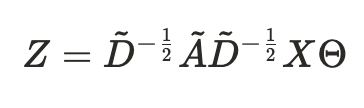

⇒ 즉 이 수식은 이웃 노드들의 특성 정보를 평균 내서 정리하고(그래프 연산), 그걸 선형 변환으로 표현한다.
⇒ 여기서 계산 복잡도는 O(|E|*C*F)
요약하자면,
GCN은 이웃 노드로부터 정보를 받아오되, 그 정보를 정규화된 방식으로 평균내고, 선형 변환 + 비선형 함수를 통해 새로운 노드 표현을 만드는 구조다.
3. Semi-Supervised Node Classification
- 다시 본론으로 돌아와서, 본 연구의 목표는 Semi-Supervised node classification이었다. 앞선 2장에서 $f(X, A)$를 정의했다. 여기서 X는 입력 피쳐, A는 그래프 구조(인접 행렬)이다.
- ⇒ 즉 GCN의 가장 큰 아이디어는 인접행렬과 노드 피쳐를 Concat한다는 것이다
- 이러한 방식으로 기존의 가정을 효율적으로 반론할 수 있다. 모델이 노드 피쳐 뿐만 아니라 그래프 구조까지 사용함으로써 정보 이득을 얻을 수 있다.
3.1 Example
- 우선 대칭적인 인접 행렬 A를 갖는 그래프에서 Semi-Supervised node classification을 위한 2층 GCN을 구현한다.
- 우선 전처리 단계에서 논문에서 제시한 정규화를 시킨다 :

- 순전파 수식은 다음과 같이 정의된다.

- W0은 입력에서 hidden layer로 가는 가중치 행렬, hidden layer층은 H개의 feature map을 지니게 된다.
- W1은 은닉층에서 출력층으로 가는 가중치 행렬이다.
- Semi Supervised Learning을 위해서 Label이 된 데이터에 대해서만 cross entropy 손실함수를 적용해준다. Y_L은 라벨이 존재하는 노드들의 인덱스 집합이다.
- 학습 가능한 파라미터는 SGD를 통해 학습된다.


3.2 Implementation
- 실험은 앞서 정의한 2-layer GCN의 forward propagation 식으로 진행이 된다.
- 시간 복잡도는 O(|E|CHF) 가 되는데, |E|는 엣지 수, C는 입력 수, H는 히든 레이어 유닛 수, F는 출력 채널 수가 된다.
4. Related Works
4.1 Graph-Based Semi Supervised Learning
- 명시적 그래프 라플라시안 정규화 방식
- Label Propagation
- Manifold Regularization
- Deep Semi Supervised Embedding
- Graph Embedding based approaches
- Deep Walk
- LINE, Node2vec
4.2 Neural Networks on Graphs
- 그래프에서 작동하는 신경망은 2005년 Gori의 연구와 2009년 Scarselli의 연구에 의해서 RNN 형태로 처음 제시되었다. 이후 Li 등이 RNN 기반의 GNN을 개선했다.
- 2015년 Duvenaud 등이 그래프에서 합성곱 유사 전파 규칙과 그래프 수준의 분류 방법을 제안했으나, 노드 차수 확장에 한계가 있었다.
- 그 외에도 Atwood의 연구는 $O(N^2)$의 시간 복잡도를 가진다는 한계가 있었고, Niepert는 그래프를 1D CNN에 입력하는 방식을 제안했다.
- 본 연구는 2014년 Bruna의 연구에 기반해서 스펙트럴 그래프 합성곱 신경망을 활용해 확장했다.
5. Experiments
5.1 Datasets
- 사용된 데이터셋은 다음과 같다.

5.2 Experimental Set Up
- 기본적으로 3.1에서 소개된 2-layer GCN을 사용한다.
- 데이터셋 분할은 2016년 Yang의 연구와 동일하게 적용하였다. 라벨링된 노드는 500개로 하이퍼파라미터 튜닝에만 사용되고 모델 학습에는 사용되지 않는다.
- 하이퍼파라미터는 모든 레이어의 드롭아웃 비율, 첫 번째 레이어의 L2, 히든 레이어의 수로 조정한다.
- Cora 데이터셋에서 하이퍼파라미터 튜닝을 실시하고 여기서의 파라미터를 그 외의 데이터셋에서도 적용한다.
- 200 에포크, Adam 옵티마이저를 사용하고 learning rate는 0.01로 설정했다.
- 기타 선행연구들을 Baseline으로 실험을 진행했다.
6. Results

괄호 안은 수렴시간까지 걸린 시간이다. 실험 결과 기존의 Baseline 모델보다 본 논문에서 제시한 GCN 방식이 가장 정확도가 높음을 볼 수 있다.

Propagation 모델에서도 본 논문이 제시한 재 정규화된 방식이 가장 높은 정확도를 보였다.



