[2025-2] 박제우 - FLAT REWARD IN POLICY PARAMETER SPACE IMPLIES ROBUST REINFORCEMENT LEARNING

https://openreview.net/forum?id=4OaO3GjP7k

Flat Reward in Policy Parameter Space Implies Robust Reinforcement...

 

강화학습은 지도학습, 비지도학습과 함께 대표적인 인공지능 모델의 학습 방법 중 하나이다. 

 

Data Point와 Label로 학습하는 기존의 방식과는 다르게 어떠한 행동을 취하는 Agent와 그 행동에 따른 Reward로 구성된다. 

 

즉 의도한 행동을 할수록 더 큰 Reward를 부여하고, 그렇지 않을 때는 Penalty를 부여함으로써, Agent를 학습시킨다. 

 

강화학습의 핵심이 되는 Markov Decision Process의 구성 요소로는 환경(State), 행동(Action), 전이 확률(Transition Probability), 보상 함수(Reward Function), 할인율(Discount Factor)가 있다. 

 

이러한 강화학습은 주로 게임 인공지능, 로봇 제어, 자율 주행, 추천 시스템 등에서 활용되고 있다. 

 

1. Introduction

강화학습의 핵심 한계로는 환경 변화에 취약하다는 문제가 항상 지적되어 왔다. 즉 환경이 조금만 변하더라도 모델 성능에 영향이 커진다. 따라서 이러한 한계를 극복하기 위해 강건 강화학습(Robust Reinforcement Learning)이 등장했다. 

 

또한 지도학습 분야에서는 강건성을 위해서 손실함수의 Flat Minima를 찾는 최적화를 진행한다. 이 인사이트를 강화학습에도 적용하여, 보상 함수 공간이 Flat해지면 모델이 더욱 강건해질 수 있음을 예측할 수 있다. 

 

기존의 선행 연구는 지도학습에서의 이러한 방식을 실험적으로 보이기는 했으나, 이론적으로 Flat Reward Function이 Robustness와 어떤 관계를 갖는지는 증명하지 못하였다. 

 

따라서 본 연구는 이러한 Flat Reward Space와 모델의 성능 간의 관계를 증명하고자 한다. 

 

예비 실험

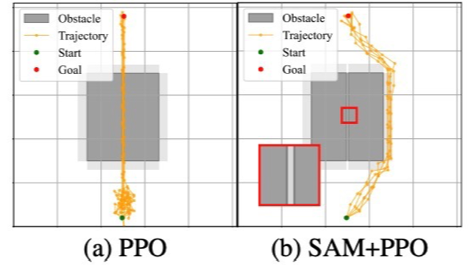
다음은 가운에 장애물을 피해서 목적지까지 최단경로를 찾는 Task이다. 

 

기존의 PPO 최적화 방식과 Flat Reward를 적용한 방식을 비교한 결과 훨씬 안전한 선택을 보였다. 

 

2. Related Works

PLASTIC: Improving Input and Label Plasticity for Sample Efficient Reinforcement Learning

 

다음 연구에서는 입력이나 보상이 달라지더라도 변화에 적응할 수 있는 능력을 Plasticity라고 정의했다. 

 

이 Plasticity를 증가시키기 위해서 SAM, Layer Normalization , CReLU, Reset 방식을 적용한 새로운 최적화 프레임워크를 제안했다. 

 

실험 결과 SAM 알고리즘에서 Plasticity가 증가함을 확인했다. 그러나 이러한 평평한 보상 지형이 성능에 왜 긍정적인 영향을 미쳤는지에 대한 증명이 부족했다. 

 

SHARPNESS-AWARE MINIMIZATION FOR EFFICIENTLY IMPROVING GENERALIZATION

 

계속해서 나오는 SAM 최적화 방식인데, 이는 모델 파라미터 세타에 대해서 약간의 perturbation 입실론을 가한 뒤, 그 손실의 최대를 최소화시키는 min man 최적화를 목적함수로 둔다.

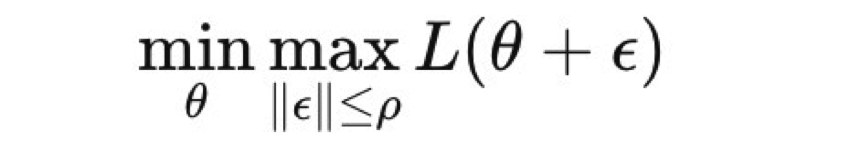
다음 수식을 보면 파라미터 세타에 대한 손실함수 L에다가 perturbation 입실론을 부여하는데, 이 입실론의 norm은 p로 제한된다. 

 

따라서 일정 주변 구간 내에서 손실함수를 극대화시키는 지점을 찾아서 그 지점을 최소화시키는 방식으로 손실함수 공간을 Flat하게 만든다. 

 

3. Preliminaries

MDP(Markov Decision Process)란 강화학습 모델의 기반이 되는 개념으로 <S, A, P, R, r> 같은 튜플로 표현된다. 

다음 수식은 보상 함수를 구성하는 벨만 방정식으로, State S에서 정책 파이에 따라 행동 A를 취했을 때의 누적 보상합을 나타낸다. 

 

할인률 감마는 미래 보상의 중요도를 반영하는 계수이다. 

 

또한 전이 확률은 정책에 따라 특정 행동을 취했을 때 그 행동을 실행하게 되는 확률이다. 

 

이러한 전이확률로 인한 강건성을 향상시키기 위해 등장한 개념이 Robust MDP이다. 아래 수식을 참조하면, 하나의 전이확률을 사용하는 대신 전이확률 집합을 가정하고, 그 중 최악의 성능을 보여주는 상황을 가정하고, 그 상황에서 보상을 최대화시키는 방식이다. 

 

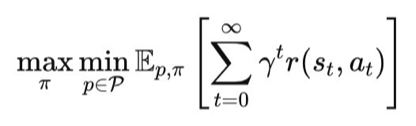
4. Linking Flat Reward to Action Robustness 

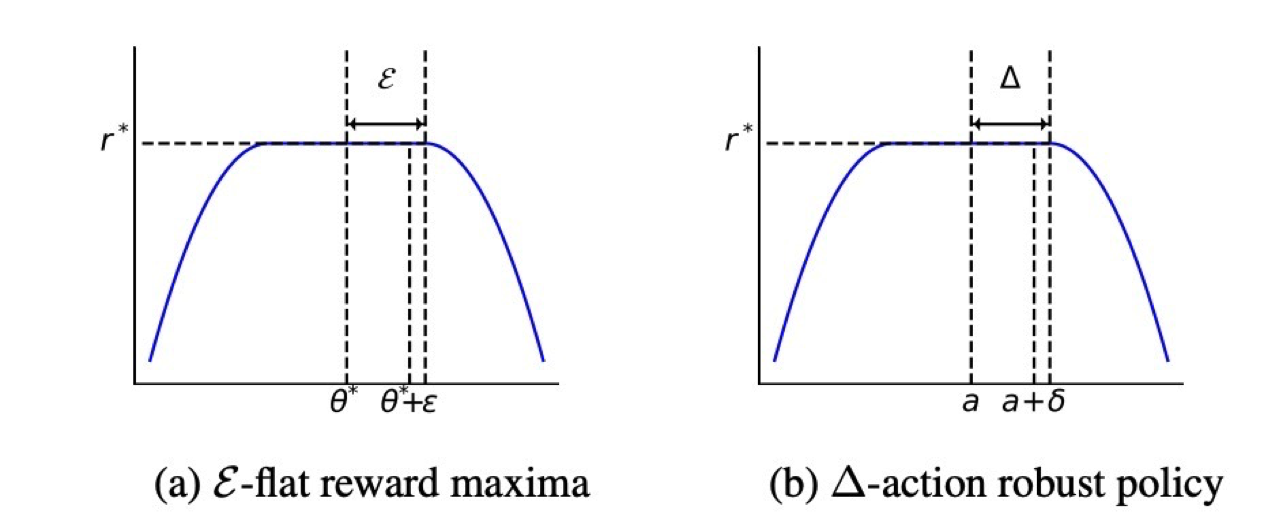
Definition 1

임의의 파라미터 교란 입실론에 대해 그 크기가 일정 수준 이하일 경우, 교란된 정책을 따라 행동하더라도 기대 누적 보상은 여전히 r* 이지만 그 수준을 벗어날 경우 교란은 보상을 떨어뜨리게 된다. 

 

Definition 2

perturbation으로 인해 생긴 행동 교란의 크기가 델타 이하일 경우 그 교란이 더해지더라도 보상이 r*로 유지된다. 즉 작은 오차에 대해서는 성능이 떨어지지 않는다. 

 

여기서 Proposition을 수식으로 표현하자면

다음과 같다. 즉 perturbation으로 인한 행동 변화 델타가 파라미터 세타에 대한 야코비안 행렬과 perturbation의 곱 이하일 때, Reward가 유지된다는 뜻이다. 

 

Proof

먼저 정책은 다음과 같이 가우시안 분포로 가정한다. 

다음 증명에서 등장하는 세타*는 max min 최적화를 통해 도출한 Flat Reward를 갖는 정책 파라미터이다. 

 

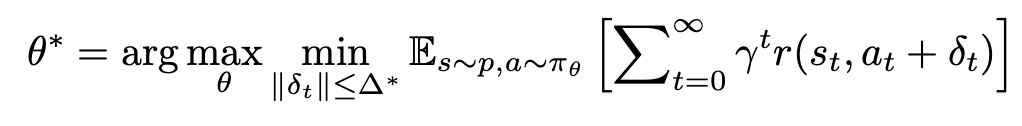
이 후 파라미터 세타*에 대한 평균 행동을 뮤라고 할 때, 교란 입실론에 대한 1차 테일러 전개를 통해 다음과 같이 행동 교란 및 범위를 정의할 수 있다. 

또한 가우시안 분포의 특성상 다음을 만족한다. 

즉 정책에 대한 교란을 행동에 대한 변화로 이동시켜서 해석할 수 있다는 뜻이다. 

 

이를 Definition 1과 연관지어서 생각하면 그 보상 함수에 대한 수식을 정책 파이에 대한 perturabtion 입실론을 행동에 대한 변화량 델타로 다시 쓸 수 있다. 

입실론에 대한 변화량을 다음과 같이 델타로 나타내면 이는 Definition 2와 이어진다. 

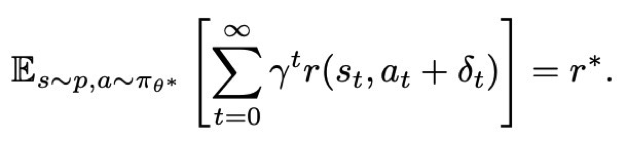
따라서 이 과정을 통해 Definition 1과 2의 연관성에 대해 설명할 수 있다. 

5. Experimental Results

본 연구는 이러한 Flat Reward와 성능간의 연관성을 실험적으로 입증하기 위해 MuJoCo task Experiment를 진행했다. 

 

• HalfCheetah-v3, Hopper-v3, Walker2d-v3를 통한 실험

• PPO, RNAC, RARL 알고리즘과 SAM+PPO를 비교

• 각 모델은 3층 MLP구조 사용, PPO와 SAM+PPO는 동일한 하이퍼 파라미터, RNAC와 RARL은 논문 구조를 따름

 

MuJoCo 환경이란 강화학습에서 로봇 제어 실험 환경으로 사용하는데, 다관절 로봇의 동역학을 정밀하게 시뮬레이션 할 수 있는 프레임워크이다. 이는 정책의 강건성 성능 평가에 적합하다고 알려져 있다. 특히 질량, 마찰, 노이즈 등을 반영하고 이러한 perturbation이 결과에 유발하는 차이를 쉽게 확인할 수 있다. 

 

본 논문에서 사용한 Flat Reward를 사용하는 모델은 SAM+PPO방식이다. 노이즈가 증가할수록 네 알고리즘이 모드 성능이 감소하나, SAM+PPO 방식이 그 와중에서 가장 높은 성능을 보이고, 경사 또한 완만했다. 

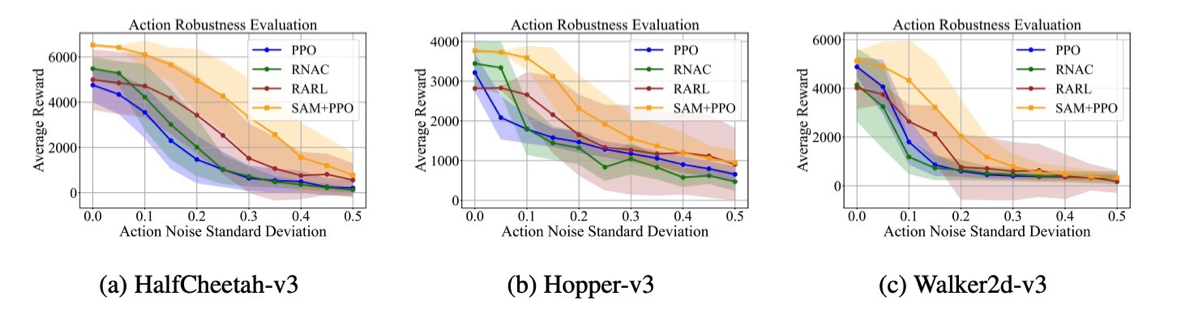
마찰, 질량 등에 대해서 노이즈를 가했을 때도 SAM+PPO 방식이 거의 가장 높은 성능과 강건성을 보였다. 

수치적으로 확인했을 때도 대부분의 환경에서 노이즈가 가해졌을 때 SAM + PPO 방식이 성능 저하가 가장 낮은 것을 볼 수 있다. 

 

보상 함수 지형과 그 평탄한 정도를 시각화했을 때도 마찬가지로 확인이 가능하다. 

 

다만