5.1 계산 그래프
계산 그래프는 계산 과정을 그래프로 나타낸 것이다. 여기에서의 그래프는 그래프 자료구조로, 복수의 노드와 에지로 표현된다.
이번 절에서는 계산 그래프에 친숙해지기 위한 간단한 문제를 풀어볼 것이다.
간단한 문제를 풀어본 이후 오차역전파법까지 도달할 것이다.
5.1.1 계산 그래프로 풀다
그럼 간단한 문제를 계산 그래프를 사용해서 풀어보자.
곧 보게 될 문제는 암산으로도 풀 정도로 간단하지만 지금의 목적은 계산 그래프에 익숙해지는 것이다.
문제 1: 현빈 군은 슈퍼에서 1개에 100원인 사과를 2개 샀습니다.
이 때 지불 금액을 구하세요. 단, 소비세가 10% 부과됩니다.
계산 그래프는 계산 과정을 노드와 화살표로 표현한다. 노드는 원(O)으로 표기하고, 원 안에 연산 내용을 적는다.
또, 계산 결과를 화살표 위에 적어 각 노드의 계산 결과가 왼쪽에서 오른쪽으로 전해지게 한다.
문제 1을 계산 그래프로 풀면 [그림 5-1]처럼 된다.
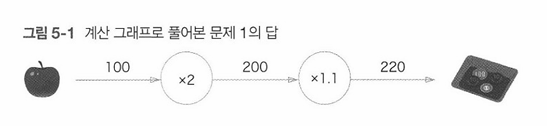
-[그림 5-1]과 같이 처음에 사과의 100원이 'x2' 노드로 흐르고, 200원이 되어 다음 노드로 전달된다.
이제 200원이 'x1.1'노드를 거쳐 220원이 된다. 따라서 이 계산 그래프에 따르면 최종 답은 220원이 된다.
다음 문제를 보게되면
문제 2: 현빈 군은 슈퍼에서 사과를 2개, 귤을 3개 샀습니다.
사과는 1개에 100원, 귤은 1개 150원입니다.
소비세가 10%일 때, 지불 금액을 구하세요
이 때의 계산 그래프는 [그림 5-3]처럼 된다.

지금까지 살펴본 것처럼 계산 그래프를 이용한 문제풀이는 다음 흐름으로 진행한다.
1. 계산 그래프를 구성한다.
2. 그래프에서 계산을 왼쪽에서 오른쪽으로 진행한다.
여기서 2번째 '계산을 왼쪽에서 오른쪽으로 진행'하는 단계를 순전파라고 한다.
순전파는 계산 그래프의 출발점부터 종착점으로의 전파이다.
순전파라는 이름이 있다면 반대 방향의 전파도 가능할까?
그렇다. 그것을 역전파라고 한다. 역전파는 이후에 미분을 계산할 때 중요한 역할을 한다.
5.1.2 국소적 계산
계산 그래프의 특징은 '국소적 계산'을 전파함으로써 최종 결과를 얻는다는 점에 있다.
국소적 계산은 결국 전체에서 어떤 일이 벌어지든 상관없이 자신과 관계된 정보만으로
결과를 출력할 수 있다는 것이다.
가령 슈퍼마켓에서 사과 2개를 포함한 여러 식품을 구입하는 경우를 생각해보자.
이를 [그림 5-2]와 같은 계산 그래프로 나타낼 수 있을 것이다.

[그림 5-4]에서는 여러 식품을 구입하여 (복잡한 계산을 거쳐) 총금액이 4000원이 되었다.
여기에서 핵심은 각 노드에서의 계산은 국소적 계산이라는 점이다.
가령 사과와 그 외의 물품 값을 더하는 계산(4000+200 -> 4200)은 4000이라는 숫자가 어떻게 계산되었느냐와는
상관없이, 단지 두 숫자를 더하면 된다는 뜻이다.
각 노드는 자신과 관련한 계산(이 예에서는 입력된 두 숫자의 덧셈) 외에는 아무것도 신경 쓸게 없다.
- 국소적인 계산은 단순하지만, 그 결과를 전달함으로써 전체를 구성하는
복잡한 계산을 해낼 수 있다.
5.1.3 왜 계산 그래프로 푸는가?
계산 그래프를 사용하는 가장 큰 이유는 역전파를 통해 '미분'을
효율적으로 계산할 수 있는 점에 있다.
- 계산 그래프의 역전파를 설명하기 위해 문제 1을 다시 꺼내보자.
문제 1은 사과를 2개 사서 소비세를 포함한 최종 금액을 구하는 것이었다.
여기서 가령 사과 가격이 오르면 최종 금액에 어떤 영향을 끼치는지를 알고 싶다고 하자.
이는 '사과 가격에 대한 지불 금액의 미분'을 구하는 문제에 해당한다.
기호로 나타낸다면 사과 값을 x, 지불 금액을 L이라 했을 때, oL/ox 을 구하는 것이다.
이 미분 값은 사과 값이 '아주 조금' 올랐을 때, 지불 금액이 얼마나 증가하느냐를 표시한 것이다.
- 앞에서 말했듯이 '사과 가격에 대한 지불 금액의 미분' 같은 값은 계산 그래프에서 역전파를 하면 구할 수 있다.
먼저 결과만을 나타내면 [그림 5-5]처럼 계산 그래프 상의 역전파에 의해서 미분을 구할 수 있다.
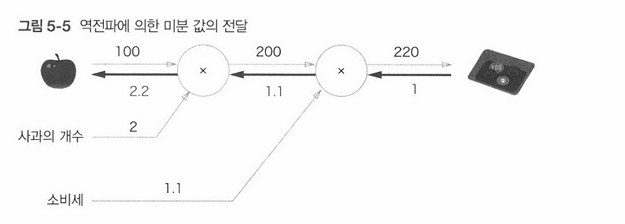
[그림 5-5]와 같이 역전파는 순전파와는 반대 방향의 화살표(굵은 선)로 그린다.
이 전파는 '국소적 미분'을 전달하고 그 미분 값은 화살표의 아래에 적는다.
이 예에서 역전파는 오른쪽에서 왼쪽으로 '1 -> 1.1 -> 2.2' 순으로 미분 값을 전달한다.
이 결과로부터 '사과 가격에 대한 지불 금액의 미분'값은 2.2라 할 수 있다.
사과가 1원 오르면 최종 금액은 2.2원 오른다는 뜻이다.
이처럼 계산 그래프의 이점은 순전파와 역전파를 활용해서 각 변수의 미분을 효율적으로 구할 수 있다는 것이다.
퀴즈
1. 계산 그래프에서 각 노드는 자신과 관련된 계산만 수행하고 결과를 전달한다는 개념은?
5.6.1 Affine/Softmax 계층 구현하기
신경망의 순전파에서는 가중치 신호의 총합을 계산하기 때문에 행렬의 곱(넘파이에서는 np.dot())을 사용한다.
import numpy as np
X = np.random.rand(2) # 입력
W = np.random.rand(2, 3) # 가중치
B = np.random.rand(3) # 편향
X.shape
W.shape
B.shape
Y = np.dot(X, W) + B
print(X.shape,W.shape, B.shape,Y.shape)
# (2,) (2, 3) (3,) (3,)
신경망의 순전파 때, 수행하는 행렬의 곱은 기하학에서 어파인변환(어파인 계층) 이라고 한다.
행렬의 곱 계산은 대응하는 차원의 원소 수를 일치시키는 게 핵심이다.
예를 들어 X와 W의 곱은 아래 그림처럼 대응하는 차원의 원소 수를 일치시켜야 한다.

앞에서 수행한 계산(행렬의 곱과 편향의 합)을 계산 그래프로 그려보고 곱을 계산하는 노드를 'dot' 이라고 하면 아래 그림과 같다. 또한, 각 변수의 이름 위에 그 변수의 형상도 표기한다.

X,W,B는 행렬(다차원 배열)이다. 지금까지의 계산 그래프는 노드 사이에 '스칼라값' 이 흘렀는 데 반해, 이 예에서는 '행렬'이 흐르고 있는 것이다.
이제 위 5-24그림의 역전파에 대해 생각해본다면 행렬을 사용한 역전파도 행렬의 원소마다 전개해보면 스칼라값을 사용한 지금까지의 계산 그래프와 같은 순서로 생각할 수 있고 전개하면 다음 식이 도출된다.
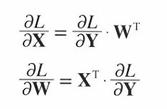
위 식에서 T는 전치행렬을 뜻한다. 전치행렬은 (i,j) 의 원소를 (j, i)의 위치로 바꾸는 것을 말한다.
W의 형상이 (2,3)이었다면 (3,2)가 된다.
위 역전파 전개 식을 바탕으로 계산 그래프의 역전파를 구해본다면 결과는 아래와 같다.
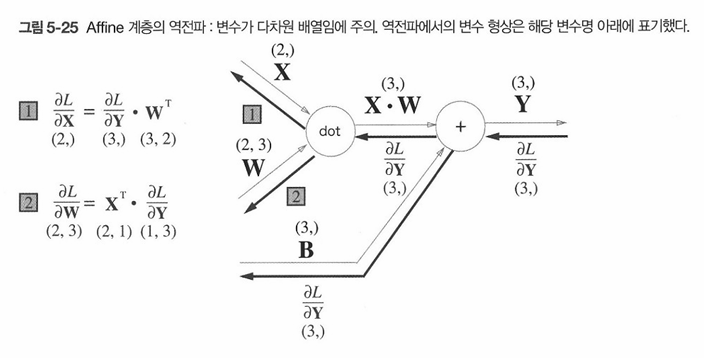
X, W와 계산 그래프의 식들은 같은 형상으로 대치된다.
행렬의 곱에서는 대응하는 차원의 원소 수를 일치시켜야 하기 때문에 행렬의 형상에 주의해야 한다.
5.6.2 배치용 Affine 계층
지금까지 설명한 Affine 계층은 입력 데이터로 X하나만을 고려한 것이었다. 이번 절에서는 데이터 N개를 묶어 순전파하는 경우, 즉 배치용 Affine 계층을 생각해보기로 한다. (배치란 묶은 데이터를 의미한다)
배치용 Affine 계층을 계산 그래프로 그리면 아래 5-27그림과 같다.
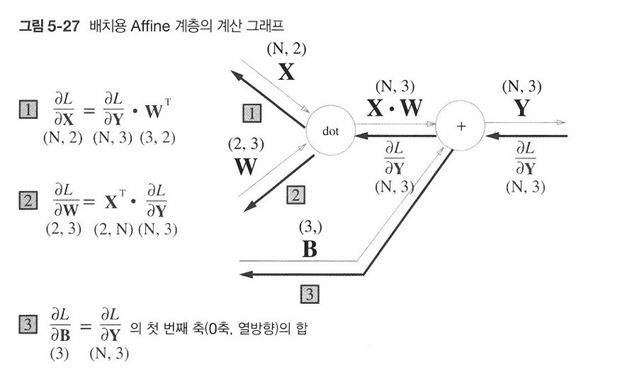
기존과 다른 부분은 입력인 X의 형상이 (N,2) 가 된 것뿐이다. 그 뒤로는 지금까지와 같이 계산 그래프의 순서를 따라 순순히 행렬 계산을 하게 된다.
편향을 더할 때 주의해야 한다. 순전파 때의 편향 덧셈은 X W에 대한 편향이 각 데이터에 더해진다.
예를 들어 N=2(데이터가 2개)로 한 경우, 편향은 그 두 데이터 각각에 더해진다.
X_dot_W = np.array([[0, 0, 0], [10, 10, 10]])
B = np.array([1, 2, 3])
print(X_dot_W)
print(X_dot_W + B)
[[ 0 0 0]
[10 10 10]]
[[ 1 2 3]
[11 12 13]]
순전파의 편향 덧셈은 각각의 데이터에 더해진다. 그래서 역전파 때는 각 데이터의 역전파 값이 편향의 원소에 모여야하고 코드는 다음과 같다.
dY = np.array([[1, 2, 3], [4, 5, 6]])
print(dY)
dB = np.sum(dY, axis=0) # 행 방향 연산
print(dB)
[[1 2 3]
[4 5 6]]
[5 7 9]
이 예에서는 데이터가 2개라고 가정한다. 편향의 역전파는 그 두 데이터에 대한 미분을 데이터마다 더해서 구한다.
그래서 np.sum()에서 0번째 축(데이터를 단위로 한 축)에 대해서 (axis = 0)의 총합을 구하는 것이다.
이상의 Affine 구현은 다음과 같다.
import numpy as np
class Affine:
def __init__(self, W, b):
self.W = W # 가중치
self.b = b # 편향
self.x = None # 입력
self.dW = None # 가중치에 대한 기울기
self.db = None # 편향에 대한 기울기
def forward(self, x):
self.x = x # 입력값을 저장
out = np.dot(x, self.W) + self.b # 선형 변환
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T) # 입력에 대한 기울기
self.dW = np.dot(self.x.T, dout) # 가중치에 대한 기울기
self.db = np.sum(dout, axis=0) # 편향에 대한 기울기
return dx
5.6.3 Softmax-with-loss계층
마지막으로 출력층에서 사용하는 소프트맥스 함수에 관해 알아본다. 소프트맥스 함수는 입력 값을 정규화해서 출력한다.
예를 들어 손글씨 숫자 인식에서의 Softmax 계층의 출력은 아래 그림 5-28처럼 된다.

위와 같이 Softmax 계층은 입력 값을 정규화(출력의 합이 1이 되도록 변형) 하여 출력한다.
Softmax는 지수 함수를 사용하고 입력 값이 커질수록 기하급수적으로 증가한다.
즉, Softmax는 가장 큰 점수에 대해 매우 높은 확률을 부여하고, 나머지는 거의 0에 가깝게 만든다.
또한, 손글씨 숫자는 가짓수가 10개(10클래스 분류)이므로 Softmax 계층의 분류는 10개가 된다.
이제 소프트맥스 계층을 구현할 텐데, 손실 함수인 교차 엔트로피 오차도 포함하여 구현한다.
계산 그래프를 살펴보면 다음 5-29 그림과 같다.
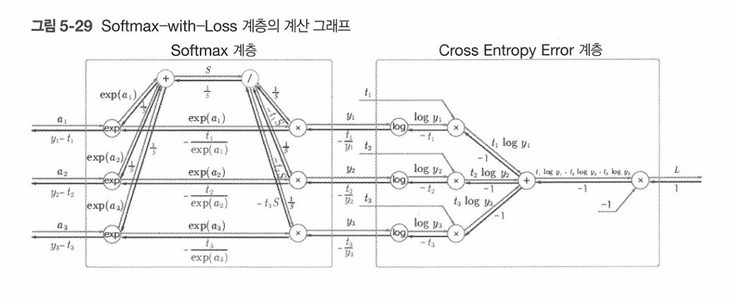
그림 5-29의 그래프는 5-30으로 간소화할 수 있다.

그림 5-30에서 주목할 것은 역전파의 결과이다. Softmax 계층의 역전파는 (y1 - t1, y2-t3, y3 - t3)라는 말끔한 결과를 내놓고있다.
y는 Softmax 계층의 출력이고, t는 정답 레이블이기에 (y1 - t1, y2-t3, y3 - t3) 결과는 Softmax 계층의 출력과 정답 레이블의 차분이라고 할 수 있다. 신경망의 역전파에서는 이 차이인 오차가 앞 계층에 전해진다.
그런데 신경망 학습의 목적은 신경망의 출력(Softmax의 출력)이 정답 레이블과 가까워지도록 가중치 매개변수의 값을 조정하는 것이었다. 그래서 신경망의 출력과 정답 레이블의 오차를 효율적으로 앞 계층에 전달해야 한다.
(y1 - t1, y2-t3, y3 - t3) 결과는 바로 Softmax 계층의 출력과 정답 레이블의 차이로, 신경망의 현재 출력과 정답 레이블의 오차를 있는 그대로 드러내는 것이다.
구체적인 예를 보도록 하자.
가령 정답 레이블이 (0,1,0)일 때 Softmax계층이 (0.3,0.2,0.5)를 출력했다고 해보고 정답 레이블의 정답 인덱스는 1이다.
그런데 출력에서는 이때의 확률이 겨우 20%라서 이 시점의 신경망은 제대로 인식하지 못한다.
이 경우 Softmax 계층의 역전파는 (0.3,-0.8,0.5)라는 커다란 오차를 전파한다.
결과적으로 Softmax 계층의 앞 계층들은 그 큰 오차로부터 큰 깨달음을 얻게 된다.
또다른 예를 살펴보면 정답 레이블이 똑같이 (0,1,0)일 때 Softmax 계층이 (0.01,0.99,0)을 출력한 경우이다.
이 경우 Softmax 계층의 역전파가 보내는 오차는 비교적 작은 (0.01, -0.01, 0)이다. 이번에는 앞 계층으로 전달된 오차가 작으므로 학습하는 정도도 작아진다.
아래는 Softmax-with-Loss 계층을 구현한 코드이다.
class SoftmaxwithLoss:
def __init__(self):
self.loss = None # 손실
self.y = None # softmax의 출력
self.t = None # 정답 레이블(원-핫 벡터)
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_loss(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
return dx
Affine과 마찬가지로 softmax()와 cross_entropy_error()을 이용했다. 또 역전파 때는 전파하는 값을 배치의 수(batch_size)로 나눠서 데이터 1개당 오차를 앞 계층으로 전파하는 점에 주의하자.
SoftmaxwithLoss로 MNIST 예측하기
import numpy as np
import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical
# MNIST 데이터셋 불러오기
(x_train, t_train), (x_test, t_test) = mnist.load_data()
# 이미지 데이터 전처리: 28x28 이미지를 1D 벡터로 변환하고, 정규화
x_train = x_train.reshape(-1, 28*28).astype(np.float32) / 255.0
x_test = x_test.reshape(-1, 28*28).astype(np.float32) / 255.0
# 레이블을 one-hot 인코딩
t_train = to_categorical(t_train, 10)
t_test = to_categorical(t_test, 10)# 임의의 가중치 초기화
W = np.random.randn(784, 10) * 0.01 # 784는 28x28, 10은 클래스 개수
b = np.zeros(10)
# 학습을 위한 하이퍼파라미터
learning_rate = 0.1
epochs = 10
batch_size = 128
# Softmax with Loss 객체 생성
loss_layer = SoftmaxwithLoss()
# 학습 시작
for epoch in range(epochs):
for i in range(0, x_train.shape[0], batch_size):
# 미니배치 생성
x_batch = x_train[i:i+batch_size]
t_batch = t_train[i:i+batch_size]
# Forward pass (선형 변환 후 softmax)
out = np.dot(x_batch, W) + b # 선형 변환 (W * x + b)
loss = loss_layer.forward(out, t_batch)
# Backward pass
dout = 1 # 일반적으로 loss에 대한 기울기를 1로 설정
dx = loss_layer.backward(dout)
# 경사 하강법을 이용한 가중치 업데이트
W -= learning_rate * np.dot(x_batch.T, dx)
b -= learning_rate * np.sum(dx, axis=0)
print(f'Epoch {epoch + 1}, Loss: {loss}')
# 테스트 데이터로 평가
y_test = softmax(np.dot(x_test, W) + b) # 테스트 데이터에 대해서도 선형 변환 후 softmax 적용
predictions = np.argmax(y_test, axis=1) # 예측된 레이블
accuracy = np.sum(predictions == np.argmax(t_test, axis=1)) / x_test.shape[0]
print(f'Test Accuracy: {accuracy * 100:.2f}%')
Epoch 1, Loss: 0.4477563898044917
Epoch 2, Loss: 0.3887865931271004
Epoch 3, Loss: 0.3650096536200962
Epoch 4, Loss: 0.3512761033822637
Epoch 5, Loss: 0.34185674814394157
Epoch 6, Loss: 0.3347217947295818
Epoch 7, Loss: 0.32896941840316846
Epoch 8, Loss: 0.32413671616683304
Epoch 9, Loss: 0.3199599898196626
Epoch 10, Loss: 0.3162763699521937
Test Accuracy: 92.11%

퀴즈
1. X.shape = (5, 10), W.shape = (10, 20), B.shape = (20,)인 경우, Y = np.dot(X, W) + B의 Y.shape의 결과는?
'Miscellaneous' 카테고리의 다른 글
| [2025-1] 박제우 - Deep Anomaly Detection with Deviation Networks (0) | 2025.04.06 |
|---|---|
| [2025-1] 정성윤 - Visualizing the Loss Landscape of Neural Nets (1) | 2025.03.30 |
| [2025-1] 윤선우 - 밑바닥부터 시작하는 딥러닝 리뷰, (CH 5.3, 4) 역전파, 단순한 계층 구현하기 (1) | 2025.03.26 |
| [2025-1] 박경태 - 밑바닥부터 시작하는 딥러닝 리뷰, (CH 5.5) 활성화 함수 계층 구현하기 (0) | 2025.03.26 |
| [2025-1] 박경태 - 밑바닥부터 시작하는 딥러닝 리뷰, (CH 5.2) 연쇄 법칙 (0) | 2025.03.26 |



