[2025-1] 최민서 - Maximum Likelihood Training of Score-Based Diffusion Models

[논문링크] https://arxiv.org/abs/2101.09258

Maximum Likelihood Training of Score-Based Diffusion Models

 

[Score-based diffusion models 논문리뷰] https://blog.outta.ai/270

[2025-1] 최민서 - Score-based Generative Modeling through Stochastic Differential Equations

해당 논문에서 제안된 모델을 score-based diffusion model이라 명명한다. 위 논문을 읽어보지 않았다면 밑의 내용을 이해하기 힘들 수 있다.

 

1. Introduction

 

Score-based diffusion model은 forward SDE를 통해 데이터를 perturb한 후, reverse SDE를 통해 tractable한 분포로부터 원본 데이터를 샘플링한다. 신경망 모델은 score, 즉 $\nabla_{\mathbf{x}}\mathrm{log}p_t(\mathbf{x})$을 근사하도록 학습시킨다. 

 

이러한 학습 방식은 직접 negative log-likelihood(NLL)을 구해 최소화하는 학습 방식보다 학습이 용이하다. 하지만 이러한 학습 방식은 모델의 NLL을 직접적으로 낮추는 학습방식은 아니기 때문에 NLL을 최소화했다고 말하기는 힘들다.

 

낮은 NLL 값을 갖는 모델은 많은 이점을 갖는다. 따라서 본 논문에서는 NLL을 upper bound하는 training objective을 제시하여 모델의 학습이 NLL을 감소에 직접적으로 영향을 줌을 증명한다. 이는 기존의 training objective의 시간 계수 $\lambda(t)$를 특정한 값으로 설정하여 얻는다.

 

2. Score-Based Diffusion Models

 

Score-based diffusion model은 forward SDE, reverse SDE로 구성된다.

 

2.1 Diffusing Data to Noise with an SDE

 

Forward SDE는 아래와 같이 나타난다.

 

$$d\mathbf{x} = \mathbf{f}(\mathbf{x},t)dt + g(t)d\mathbf{w}$$

 

$d\mathbf{w}$는 infinitesimal Gaussian noise라 생각하면 된다.

 

Score-based diffusion model에서는 $f$와 $g$에 어떤 함수를 주느냐에 따라 VE SDE, VP SDE, Sub-VP SDE로 나뉜다.

 

앞으로 확률분포를 아래와 같이 명명한다.

$p_t(\mathbf{x})$ : Marginal distribution of $\mathbf{x}(t)$

$p_{0t}(\mathbf{x}\prime | \mathbf{x})$ : Transition distribution from $\mathbf{x}(0)$ to $\mathbf{x}(t)$

$\pi(\mathbf{x})$ : Some analytically tractable prior distribution (Gaussian distribution) 

 

2.2 Generating Samples with the Reverse SDE

 

Reverse SDE는 아래와 같이 나타난다.

 

$$ d\mathbf{x} = [\mathbf{f}(\mathbf{x},t) - g(t)^2 \nabla_\mathbf{x} \mathrm{log}\,p_t(\mathbf{x})]dt + g(t)d\bar{\mathbf{w}} $$

 

Reverse SDE에서 $dt$는 negative time step으로 $t=T$부터 $t=0$까지 방정식이 진행된다. 위 SDE를 따라 $\mathbf{x}(T) \sim p_T(\mathbf{x})$에서 시작하여 $t$에서의 확률분포 $p_t(\mathbf{x})$를 구해보면, forward SDE에서 구한 분포와 동일하게 나온다.

 

학습은 아래의 training objective을 최소화하는 방향으로 진행된다.

 

$$ \mathcal{J}_{SM}(\theta;\lambda(\cdot)) := \frac{1}{2} \int_{0}^{T} \mathbb{E}_{p_{t}(x)}\bigl[\lambda(t) \Vert \nabla_x \log p_{t}(x), s_{\theta}(x,t)\Vert_2^2\bigr]\,dt$$

 

Denoising score matching(DSM) 기법을 사용하여 아래와 같은 training objective을 구할 수 있다.

 

$$J_{\mathrm{DSM}}(\theta;\lambda)=\frac12\int_0^T\mathbb{E}_{p_t(\mathbf{x})\,p_{0t}(\mathbf{x}'\mid \mathbf{x})}\bigl[\|\lambda(t)\nabla_{\mathbf{x}'}\log p_{0t}(\mathbf{x}'\mid \mathbf{x})-s_{\theta}(\mathbf{x}',t)\|^2\bigr]\,dt$$

 

$\mathbf{f}$가 linear인 경우, $p_{0t}(\mathbf{x}'|\mathbf{x})$가 정규분포로 나오기 때문에 계산이 용이하다.

 

이렇게 학습시킨 $s_\theta(\mathbf{x},t)$를 reverse SDE에 넣어 샘플을 생성할 수 있다.

 

3. Likelihood of Score-Based Diffusion Models

 

학습시킨 모델 $s_\theta(\mathbf{x},t)$을 이용하여 Reverse SDE를 통해 생성되는 최종 확률분포를 $p_\theta^{SDE}(\mathbf{x})$라 하자. $p_\theta^{SDE}(\mathbf{x})$는 tractable한 분포 $\pi$로부터 reverse SDE에 따라 생성되는 샘플들을 이용하여 그 분포를 추정할 수 있다.

 

$p_\theta^{ODE}$는 아래의 probability flow ODE를 통해 구해지는 최종 확률분포이다.

 

$$\frac{d\mathbf{x}}{dt}\;\bigl[f(\mathbf{x},t)-\tfrac12\,g(t)^2\,\nabla_\mathbf{x}\log p_t(\mathbf{x})\bigr].$$

 

$p_\theta^{ODE}$는 $p_\theta^{SDE}$와 달리 ODE solver를 이용하여 정확한 확률 분포를 구할 수 있다. 하지만 $p_\theta^{ODE}$의 NLL을 직접적으로 낮추는 방식으로 학습을 할 경우, 매 batch마다 ODE solver를 이용해 $p_\theta^{ODE}$ 값을 직접 계산해야 하므로 계산량이 매우 많아진다.

 

$p_\theta^{SDE}$는 임의의 data point에 대해 값을 예측할 수조차 없기 때문에, $p_\theta^{SDE}$의 값을 직접 낮추는 방식으로 학습하는 것 자체가 불가능하다.

 

즉, 본 논문에서는 NLL의 값을 낮추는 training objective를 찾고 싶은 것인데, 위와 같이 $p_\theta^{ODE}$나 $p_\theta^{SDE}$의 값을 training objective로 잡아 이를 직접 낮춰 최적화 시키는 것은 불가능하다고 설명하고 있다.

 

4. Bounding the Likelihood of Score-Based Diffusion Models

 

높은 log likelihood를 가지는 모델은 굉장히 좋은 성질을 많이 가진다. 하지만 기존의 score-based diffusion model은 직접 NLL을 낮추는 방식(ELBO 등)을 사용하지 않아 학습이 잘 되었다고 NLL이 낮아졌다고 할 수 없다. 또한 section 3에서 본 것 같이, 직접 NLL을 training objective으로 사용하는 것 또한 불가능하다.

 

따라서 본 논문에서는 section 3에서 정의한 p_SDE와 p_ODE의 NLL을 upper bound하는 training objective 제시한다. 이는 기존 $\mathcal{J}_{SM}$, $\mathcal{J}_{DSM}$의 시간 계수 $\lambda(t)$를 특정 값으로 설정함으로써 달성 가능하다.

 

단순히 기존 학습 방식에서 계수만 바꾸어 준 것이기 때문에, 기존 학습의 편이성 그대로 유지할 수 있다. 또한 이후 Theorem을 통해 NLL을 낮춘다는 수학적 근거 또한 갖춘다.

 

4.1 Bounding the KL Divergence with likelihood weighting

 

NLL은 KL divergence와 같기 때문에, 아래에서는 KL divergence의 upper bound를 제시한다. 이때 계수는 $\lambda(t)=g(t)^2$로 설정한다.

$ NLL(\theta)=-\mathbb{E}[\mathrm{log}p_\theta(x)] = D_{KL}(p_{data}||p_\theta) + H(p_{data}) $이기 때문에 NLL은 KL divergence와 같다고 볼 수 있다.

 

아래 Theroem은 $\lambda(t)=g(t)^2$로 계수를 설정했을 때, $\mathcal{J}_{SM}$이 NLL을 upper bound함을 보여준다.

 

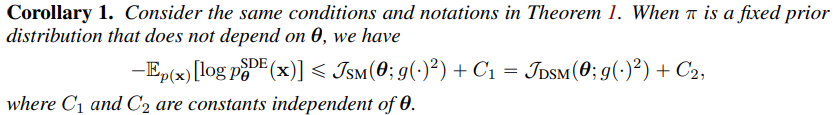
엄밀한 증명은 논문의 Appendix A에 나와있다.

 

$\lambda(t)=g(t)^2$을 likelihood weighting이라 명명한다. 기존의 score-based diffusion model에서 $\lambda(t)$는 실험적으로 설정되어, NLL과의 관계성을 증명할 수 없었다. 하지만 likelihood weighting을 통해 training objective과 NLL의 관계성을 증명했다.

 

VE, VP, Sub-VP SDE의 경우 아래와 같이 구체적으로 아래와 같이 $\lambda(t)$를 설정한다.

 

 

또한 theorem 2에서 위에서 증명한 boundness가 얼마나 tight한지 설명한다.

 

엄밀한 증명은 논문의 Appendix A에 나와있다.

 

즉 이상적인 조건 하에서, 우리의 training objective가 NLL과 같고, 심지어 p_ODE랑 p_SDE의 확률분포도 같아진다. 하지만 이는 우리의 모델이 score를 완벽하게 학습하다는 비현실적인 조건을 가지고 있어, 현실적으로는 실현 불가능하다. 즉 실제로는 $\mathcal{J}_{DSM}$을 최소화하는 학습 방식이, $p_\theta^{SDE}$의 NLL의 상한을 낮춰주기는 하지만, $p_\theta^{ODE}$의 NLL까지 낮춰준다고 할 수는 없다.

 

하지만 score model 학습이 정교할수록, $p_\theta^{ODE}$의 값은 $p_\theta^{SDE}$ 와 비슷해질 것이고 이는 실험적으로도 확인되었다.

 

4.2 Bounding the Log-Likelihood on Individual Data Points

 

4.1에서 증명한 boundness는 개별 데이터의 bound가 아니라 전체 데이터의 평균의 bound를 제시했기 때문에 학습에는 도움이 되지만, 그 외의 상황(모델의 NLL을 평가하는 상황 등)에선 도움이 되지 않는다.

 

아래의 theroem에서 데이터 별 bound를 제시한다.

 

 

엄밀한 증명은 Appendix A에 나와있다.

 

$\mathcal{L}_\theta^{SM}$과 $\mathcal{L}_\theta^{DSM}$의 각 항들은 쉽게 계산 가능하고, Monte Carlo 기법을 통해 평균과 적분값도 근사하여 구할 수 있다.

 

Theroem1과 마찬가지로 $\mathcal{L}_\theta^{SM}$과 $\mathcal{L}_\theta^{DSM}$이 $-\mathrm{log}p_\theta^{SDE}$까지 upper bound한다 보장할 수는 없다. 하지만 이론적으로 $s_\theta(\mathbf{x},t)$가 $\nabla_\mathbf{x}\mathrm{log}p_t(\mathbf{x})$를 충분히 근사하도록 학습되면, boundness도 충분히 보장될 수 있고, 이 또한 실험 과정에서 모든 데이터들에 대해 실험적으로 확인 가능했다.

 

4.3 Numerical Stability

 

지금까지 논문에서 다룬 모든 SDE는 구간 $[0,T]$에서 시간 $t$를 가졌지만, 실제로 계산을 할 때, $t$가 $0$으로 가면서 문제가 생길 수 있다. 따라서 $[0,T]$ 대신 $[\epsilon,T]$에서 값들을 구한다. 이러한 방식은 학습에는 문제가 없지만, 모델의 NLL을 구할 때 편향된 값이 나와 다른 논문의 모델들과 성능을 비교하기 어렵다. 따라서 Jensen's inequality를 이용해 값을 보정한다.

자세한 보정 과정은 Appendix B에 나와있다.

 

5. Improving the Likelihood of Score-Based Diffusion Models

 

본 섹션에서는 지금까지 논문에서 이론적으로 증명한 likelihood를 줄이는 방법들을 실험적으로 검증한다. 실험과정에서 likelihood weighting을 사용했을 때 training objective의 분산이 커짐을 확인했고, 이를 importance sampling으로 대응했는데, 자세한 과정은 section 5.1에 나와있다. 또한 5.2에서 variational dequantization을 도입하여 연속적인 모델과 이산적인 모델의 차이를 줄인다. 이러한 방법들을 적용하여 이전의 score-based diffusion model에 비해 likelihood weighting을 적용한 방식이 더 좋은 NLL 값을 가짐을 실험적으로 증명하였다.

 

5.1 Variance Reduction via Importance Sampling

 

모델을 training 시킬 때 $\mathcal{J}_{DSM}(\theta;g(t)^2)$을 최소화한다. 이 때 적분값을 계산하기 위해 Monte Carlo 기법을 사용하는데 이로 인해 직접 적분을 계산하는 것보다 빠르게 계산할 수 있지만, 값의 분산이 커지는 단점이 있다. 특히 이러한 문제점은 기존의 $\lambda(t)$를 사용할 때보다, likelihood weighting을 적용할 때 더 두드러졌다.

 

Importance sampling을 이용한 새로운 Monte Carlo 샘플링을 적용하여 아래와 같이 분산을 크게 줄일 수 있었다.

 

 

Importance sampling의 상세한 과정은 다음과 같다.

 

Score-based diffusion model의 원래 계수를 $\lambda(t)=\alpha(t)^2$이라 하자. Likelihood weighting에서는 $\lambda(t)=g(t)^2$이라 설정한다. $\alpha(t)^2$를 계수로 사용했을 때 분산이 더 낮게 나왔던 점을 이용한다. 시간 $t$에 대한 새로운 확률분포 $p(t):=\frac{g(t)^2}{\alpha(t)^2Z}$를 정의한다. 이 때 $Z$는 정규화 상수이다. $p(t)$를 이용하면 아래와 같이importance sampling을 할 수 있다.

 

$$\int_{0}^{T}g(t)^{2}h(t)\,dt = Z\int_{0}^{T}p(t)\,\alpha(t)^{2}h(t)\,dt \approx TZ\,\alpha(\tilde t)^{2}h(\tilde t)
$$

 

이 때 $\tilde{t}$는 $p(t)$에서 샘플링한 시간 $t$이다. $h(t)$에는 $\mathcal{J}_{DSM}$에서 모델과 score의 차이 값이 들어가게 된다.

 

기존에는 적분값을 평가하기 위해 $[0,T]$의 균등분포에서 $t$를 샘플링한 후, 적분값을 계산하여 $g(t)^2$에 비례하게 분산이 커졌었다. 하지만 importance sampling을 적용하여 $p(t)$에서 시간 $\tilde{t}$를 샘플링한 후 $\alpha(t)^2$을 계수로 한 loss 값을 더 적은 분산으로 구할 수 있다.

 

5.2 Variational Dequantization

 

Score-based diffusion model등의 모델은 연속적인 데이터를 가정한다. 하지만 실제로 이미지 데이터는 $[0,255]$의 이산적인 픽셀 값을 가진다. 따라서 이러한 이산적인 데이터를 변형하여 오차를 줄이는 과정이 필요하다. 가장 일반적인 방법은 각 픽셀에 $U(0,1)$의 균등분포를 더해주는 것이다. 하지만 이렇게 만들어진 이산 확률 분포 $P_\theta(\mathbf{x})$는 우리가 구하는 연속 확률 분포 $p_\theta(\mathbf{x})$를 upper bound하게 되는데, 이로 인해 직접적으로 $P_\theta(\mathbf{x})$를 최대화하는 다른 모델보다 수치에 있어서 불리할 수밖에 없다.

 

본 논문에서는 이러한 방법 대신 variational dequantization을 활용한다. $q_\phi(\mathbf{u}|\mathbf{x})$라는 새로운 학습 가능한 분포를 도입하여 아래의 training objective을 최대화한다.

 

$$\max_{\phi}\mathbb{E}_{x\sim p(x)}\mathbb{E}_{u\sim q_{\phi}(u\mid x)}\bigl[\log p_{\theta}(x+u)-\log q_{\phi}(u\mid x)\bigr]$$

 

위에서 제시한 training objective은 $\mathrm{log}P_\theta(\mathbf{x})$의 ELBO이다. 이 ELBO를 최대화하도록 $\phi$를 학습시켜 ELBO가 최대한 이산확률분포의 log likelihood인 $\mathrm{log}P_\theta(\mathbf{x})$을 근사하도록 한다.

즉, 학습 시 $\theta$의 학습과 $\phi$의 학습이 동시에 진행된다. 논문에는 나와 있지 않지만, 학습은 아래와 같이 이루어질 것이다.

1. 이산 이미지 데이터 $\mathbf{x}$를 샘플링한다.

2. $q_\phi(\mathbf{u}|\mathbf{x})$에서 $\mathbf{u}$를 샘플링하여 $\mathbf{x}$에 더해준다.

3. Dequantized data $\tilde{\mathbf{x}}$ 값과, importance sampling한 $\tilde{t}$를 이용해 $\mathcal{J}_{DSM}$을 최적화한다.

4. Variational deqauntization에 쓰이는 ELBO를 최적화한다.

 

5.3 Experiments

 

논문에서는 여러가지 데이터, 여러가지 모델을 이용하여 likelihood weighting(LW), importance sampling(IS), Variational dequantization(Var. deq.)의 효과를 교차검증하였다. 실험결과는 아래와 같다.

 

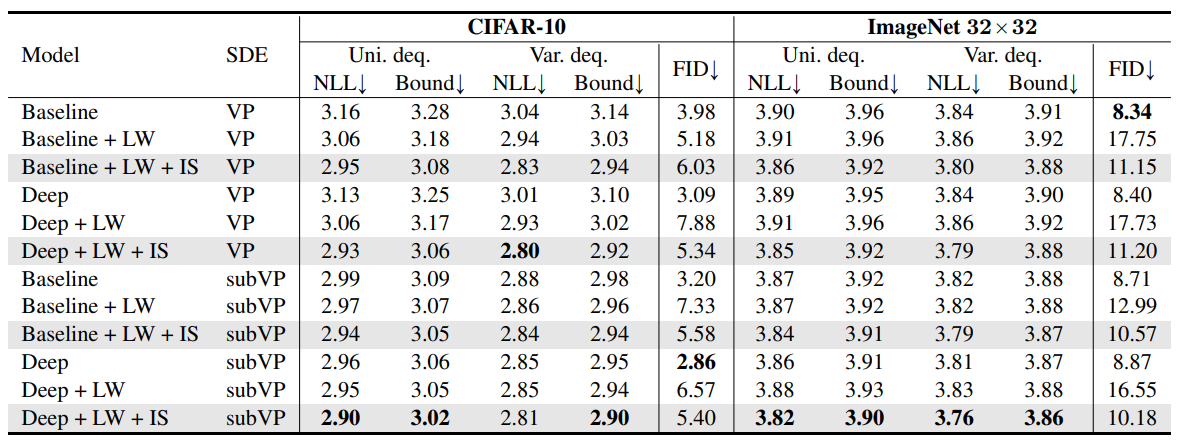
표의 NLL은 $-\mathbb{E}[\mathrm{log}p_\theta^{SDE}(\mathbf{x})]$의 값이고, Bound는 $\mathbb{E}[\mathcal{L}_\theta^{DSM}(\mathbf{x})]$의 값이다. 모델은 DDPM++, DDPM++(deep)을 사용했다.

 

주요 결과는 아래와 같다.

- Theroem 3에서는 $\mathbb{E}[\mathcal{L}_\theta^{DSM}(\mathbf{x})] \geq -\mathbb{E}[\mathrm{log}p_\theta^{SDE}(\mathbf{x})] $만을 보장했지만, 실험적으로  $\mathbb{E}[\mathcal{L}_\theta^{DSM}(\mathbf{x})] \geq -\mathbb{E}[\mathrm{log}p_\theta^{ODE}(\mathbf{x})] $도 성립함을 확인할 수 있었다.

- 대체적으로 bound가 낮아지면 NLL도 낮아졌다.

- CIFAR10에서는 LW만 추가해도 성능이 개선되었고, Imagenet32에서는 LW만 추가한 것으로는 부족했다.

- LW와 IS를 같이 사용함으로써 전반적인 모델, 데이터셋에서 NLL이 향상되었고, 약간의 FID 증가만 있었다.

- Variational dequnatization은 LW와 상관없이 전반적으로 NLL을 향상시켰다.

 

6. Conclusion

 

본 논문에서는 score-based diffusion model의 계수를 적절히 설정하여 NLL을 upper bound 할 수 있음을 이론적으로, 실험적으로 증명하였다. 또한 loss의 분산이 커지는 문제를 해결하기 위해 importance sampling을 도입했고, 이산 확률 분포의 NLL을 최대한 근사하기 위해 variational dequantization을 도입하여 모델의 NLL 성능을 향상시켰다.