[2025-1] 황징아이 - LoRA : Low Rank Adaptation of Large Language Models

논문

https://arxiv.org/pdf/2106.09685

Background

LoRA는 PEFT (Parameter-Efficient Fine Tuning)기술 중 하나입니다.

사전 학습된 LLM의 대부분의 파라미터를 Freezing하고 일부의 파라미터만을 특정 작업에 맞게 효율적으로 Fine-tuning하는 방법
적은 수의 파라미터를 학습하는 것만으로 모델 전체를 파인튜닝하는 것과 유사한 효과를 누릴 수 있도록 함

Introduction

LLM 같은 모델은 파라미터수가 매우 많아 Pre-training후, Fine-tuning 시 많은 파라미터를 학습 시켜야 하기 때문에 매우 비효율적임
이를 위해 일부 파라미터를 조정하거나 새로운 task를 위한 외부 모듈을 학습해 운영 효율성을 크게 향상시켰음
하지만 모델의 depth를 늘리거나, 모델의 사용 가능한 sequence 길이를 줄임으로써, inference latency (추론 시, 오래 걸리는 경우를 의미함)를 발생시킴
모델의 속도나 자원소모를 줄이는 대신 모델의 정확성이나 성능을 포기해야 한다는 문제 발생
저자들은 저차원의 intrinsic rank를 이용해 파인튜닝하는 방법론인 Low-Rank Adaptation (LoRA)를 제시
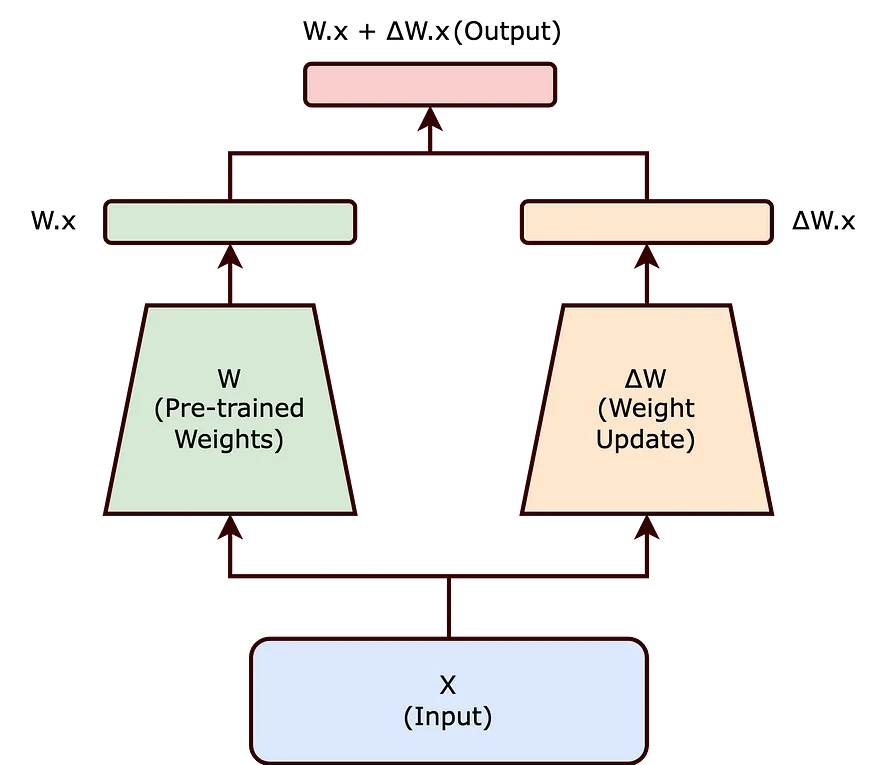
Fine-Tuning 시, 사전 학습된 모델의 weight들은 업데이트 하지 않고, LoRA의 rank decomposition matrices의 weight들만 업데이트.

Problem Statement

Fully-Fine Tuning

전체 fine-tuning 중에 모델은 사전 학습된 가중치 Φ0로 초기화되고, 조건부 언어 모델링 목적 함수를 최대화하기 위해 반복적으로 기울기를 따라 Φ0+ΔΦ(=전체 파라미터 Φ를 모두 업데이트)로 업데이트
문제는 이 업데이트가 사전 학습에도 적용되고, fine-tuning 시에도 전체 파라미터 Φ를 모두 업데이트 하는 것이 문제 = 논문에서는 각 downstream task에 대해 차원 |ΔΦ| 과 |Φ0|가 같다고 표현하였음

The Need for Parameter-Efficient Methods

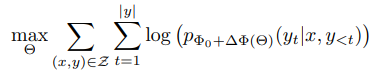
기존의 model 파라미터인 Φ를 이용해 forward를 진행한 뒤 얻어지는 ΔΦ(Φ의 gradient)를 이용해 backpropagation을 진행할 때, LoRA의 파라미터 $\Theta$를 이용. ( $|\Theta| \ll\left|\Phi_0\right|$ )
모델이 GPT-3 175B인경우 학습 가능한 파라미터의 수 $|\Theta|$ 는 $\left|\Phi_0\right|$의 0.01%정도라고 함. (활씬 효율적으로 파라미터를 업데이트할 수 있고, task specific)

Existing Solution

현재 본 연구에서 해결하고자 하는 fine-tuning 시의 문제를 해결하기위한 다양한 시도들이 있었음

Add adapter layers : Adapter라는 layer를 transformer block에 추가해주어 이 부분만 학습하는 것으로 기존 fine-tuning을 대체
Optimizing some forms of the input layer activations : Language model의 입력으로 들어갈 input vocab embedding에 prompt embedding을 추가하고, prompt embedding을 다양한 학습 방법으로 학습시키는 것으로 기존 fine-tuning을 대체

→ 대규모 및 지연에 민감한 생산 모델에는 한계

Adapter를 적용하면 비용/시간 증가
Prompt를 최적화하는 것 자체가 어렵고 sequence length의 길이가 줄어든다는 문제를 발생

Method

Low-Rank-Parametrized Update Matrices

신경망의 많은 레이어들은 행렬곱으로 이루어져 있는데, 대부분의 가중치 레이어들은 full-rank로 구성
특정 task에 적용할 때(=fine-tuning), 사전 학습된 언어 모델은 더 작은 subspace로의 랜덤 projection에도 불구하고 여전히 효율적으로 학습할 수 있으며, 낮은 내재적 차원 (intrisic dimension)을 가진다고 함
이에 영감을 받아 가중치에 대한 업데이트도 adaptation 중에 낮은 intrisic rank를 갖는다고 가정
기존 모델의 가중치 매트릭스가 dk 크기를 가질 때, 이를 dr 매트릭스 B와 r*k 매트릭스 A로 나타낼 수 있음 =>r은 d,k보다 작은 차원

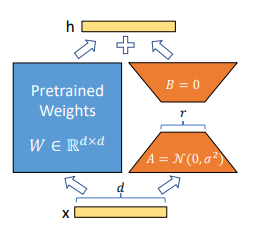
자세히 :

$x$ : $R^{1\times d}$ 의 Input ($R$ : 집합기소 실수체, 여기서는 1행 d열의 Matrix라고 이해)

$h$ : output

$W$ (blue color) : pretrained weight (사전 학습된 가중치 행렬)

$W \in R^{d\times d}$ : $W$는 $d \times d$인 실수체 $R$에 속함 (여기서는 d행d열의 Matrix라고 이해)

$A, B$ (주황색) : LoRA Adaptor (Fine Tuning 학습되는 파라미터, LoRA의 핵심!)

$A = N(0, \sigma^2)$ : A의 초기값은 정규분포 (Gaussian Noise)

$B = 0$ : B의 초기값은 0

학습하는 동안 $W_0$는 고정이 되고, 기울기 업데이트를 받지 않는 반면 $A$와 $B$는 학습 가능한 파라미터를 포함

가중치 초기화 시,

$A$는 가우시안 분포를 따르는 랜덤변수로 초기화
$B$는 0으로 초기화

차원수는 감소 (Full-Rank → R-Rank)

특정 task를 위해 LoRA 방법론으로 BA 가중치 매트릭스를 이용해 Fine-tuning 후에 다른 downstream task에 적용하고 싶은 경우, 단순히 BA 매트릭스를 B'A' 매트릭스로 바꾸는 식으로 효율적인 학습이 가능 ※ 다른 downstream task를 진행할 때마다 다른 AB 매트릭스를 사용해야 하는 한계점을 언급하였음

Experiment

Baseline
- FT: Fine-Tuning
- FTTop2: 마지막 두 레이어만 튜닝
- BitFit
- AdapH: 오리지널 adapter tuning
- AdapL: MLP 모듈 뒤와 LayerNorm 뒤에만 adapter layer
- AdapP: AdapL과 유사
- AdapD: 몇몇 adapter layer를 drop
실험 방식
- LoRA 방법론을 RoBERTa, De-BERTa, GPT-2에 적용해보고, 크기를 키워 GPT-3 175B에도 적용
- natural language understanding(NLU), natural language generation(NLG), GLUE benchmark, NL to SQL queries, SAMSum 등 다양한 downstream task에서 성능을 평가
- 모든 실험은 NVIDIA Tesla V100을 이용

Empirical Experiment

RoBERTabase, RoBERTalarge, DeBERTaXXL에 대한 GLUE 밴치마크

E2E NLG Challenge에서 다양한 adaptation 방법을 적용한 GPT-2 medium (M)과 GPT-2 Large (L) 에 대한 결과 비교

다양한 adaptation 방법을 적용한 GPT-3 175B의 성능 비교 결과

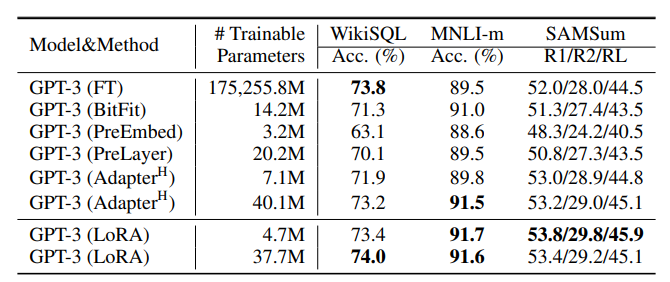
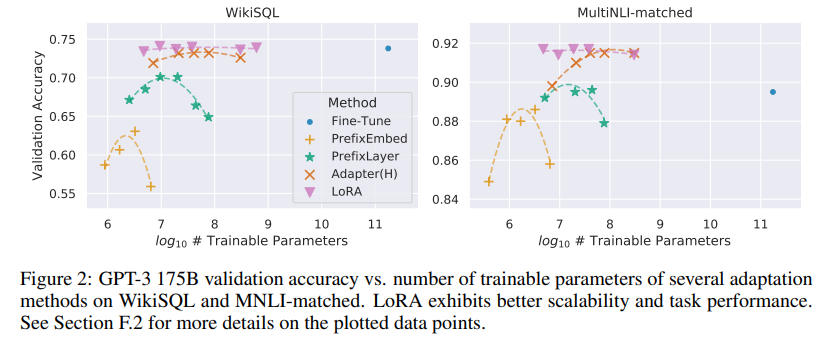
다양한 adaptation 방법을 적용한 GPT-3 175B의 정확도와 파라미터 개수에 대한 그레프

Conclusion

LoRA의 장점
- 하드웨어 및 저장 비용 절감
- 추론 속도 저하 없이 높은 모델 성능 유지
- 모델 매개변수를 공유하여 빠른 작업 가능
적용 가능성
- 주로 Transformer 기반 언어 모델에 적용.
- 밀집 레이어를 포함한 다양한 신경망에 일반적으로 적용 가능.
향후 연구 방향
1. 다른 Adaptation Technique과의 결합 가능성 탐색.
2. LoRA의 내부 메커니즘 분석 필요
3. Adaptation Weight Metrices의 체계적인 접근법 개발 필요
4. Weight Matrices의 Rank Deficiency 문제 해결 필요Background