https://youtu.be/cn7IAfgPasE?si=DA7LiUsUHAFvcvCj
Recap. optimal policy란?
state value function을 maximize하는 policy
- expected return을 최대화(과거의 action과 무관하게 앞으로 기대되는 reward를 maximize)
Recap. Bellman Equation에서 state value function을 action value function으로 나타내면


optimal policy를 구하기 위해 $V(S_t)$를 maximize할 것.
- $V(S_t)$를 maximize하는 policy $p(a_t|S_t)$를 찾으면 됨.
- $p(a_t|S_t)$는 probability distribution
그런데 $V(S_t)$를 maximize하는 과정에서 $Q(S_t,a_t)$를 보면 $p(a_{t+1}| S_{t+1}), p(a_{t+2}|S_{t+2}), ... $의 policy들이 포함되어 있다.
=>여기서 미래의 action에 대한 optimal policy들은 다 구했다고 치자.($p^{*}(a_{t+1}| S_{t+1}), p^{*}(a_{t+2}|S_{t+2}), ... $)
그리고 그렇게 $Q^{*}(S_t,a_t)$까지 maximize했다고 하자.
좀 더 자세히 설명하면,

위 식에서

이 성립하고(두번째 등호는 Markov Decision Process이기에 성립한다.)
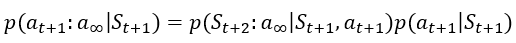
이 성립하며, 마찬가지로 Markov Decision Process이기에
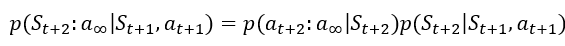
이 된다.
이를 반복하면 $p(S_{t+1}:a_{\infty}|S_t,a_t)=p(S_{t+1}|S_{t},a_{t})p(a_{t+1}|S_{t+1})p(S_{t+2}|S_{t+1},a_{t+1})p(a_{t+2}|S_{t+2})...$이 되게 되는데,
여기서 $p(S_{t+1}|S_{t},a_{t})$, $p(S_{t+2}|S_{t+1},a_{t+1})$ 등의 항은 transition probability로 환경에서 주어지는 고정된 값이고,
$p(a_{t+1}|S_{t+1})$, $p(a_{t+2}|S_{t+2})$ 등의 항은 policy에 해당하여 해당 distribution의 optimal policy를 다 찾았다고 가정하면 $Q^{*}(S_t,a_t)$가 나온다.
이 때 $V(S_t)$를 maximize하기 위해 optimal policy $p(a_{t}|S_{t})$를 찾자.
$V(S_t)$에서 $S_t$는 주어진 값이고, $a_t$는 환경에 따라 discrete할 수도, continuous한 값을 가질 수도 있다.(아래에선 continuous라고 가정)
이 때 가능한 $a_t$들 중 $Q^{*}(S_t,a_t)$가 가장 큰 $a_t$를 $a^{*}_t$라고 하면,
policy가 $a^{*}_t$를 계속 뽑아주면 된다.

즉 optimal policy $p^{*}(a_{t}|S_{t})$는 ${\delta}(a_t-a^{*}_t)$가 된다.
여기서 dirac delta function은 아래와 같은 성질을 만족하는 함수이다.
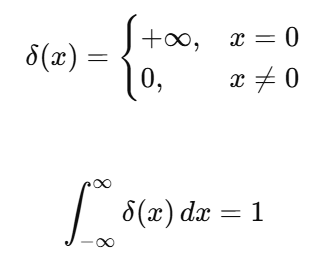
위와 같은 함수를 ${\delta}(x)$로 정의하며, 이 함수를 x축으로 a만큼 오른쪽으로 평행 이동하면 아래와 같이 된다.

즉 ${\delta}(a_t-a^{*}_t)$는 $a^{*}_t$에서만 무한대의 값을 가지는 function이라고 할 수 있다.
optimal policy $p^{*}(a_{t}|S_{t})$가 ${\delta}(a_t-a^{*}_t)$라는 것은, 정책이 $a^{*}_t$를 따르라고 유도하는 것이다.
정리하면, 현재 기대되는 return을 maximize하기 위해서는 $Q^{*}$가 주어져 있을 때 $Q^{*}$를 maximize하는 $a^{*}_t$를 고르면 된다.
이 내용은 Q-learning의 간단한 기초이다.
정리하면 Q-learning은 ${\epsilon}-greedy$를 하는데, greedy action 하는 이유는 $Q^{*}$를 maximize하는 것이 가장 좋은 policy이기 때문이다.
'Miscellaneous' 카테고리의 다른 글
| [2025-1] 김은서 - Markov Decision Process (MDP) (1) | 2025.01.05 |
|---|---|
| [2025-1] 전진우 - Monte carlo method (0) | 2025.01.04 |
| [2024-2] 문지영 - deeplearning: Deep Feedforward Networks (1) (1) | 2025.01.04 |
| [2024-2] 문지영 - deeplearning: Introduction (1) | 2025.01.04 |
| [2024-2] 박경태 - deeplearning: Probability and Information Theory (1) | 2025.01.03 |




