[2024-2] 최민서 - Deep Unsupervised Learning using Nonequilibrium Thermodynamics

https://arxiv.org/abs/1503.03585

Deep Unsupervised Learning using Nonequilibrium Thermodynamics

 

생성형 모델이 이미지를 생성하는 방식은 다양하고 그 중 하나가 diffusion(확산)을 이용하는 방법이다. 초기의 복잡한 데이터셋의 각 데이터 포인트들을 확산시켜 다루기 쉬운 데이터 분포로 변환하는 방식은 본 논문에서 처음 제시된 방식으로 비평형 열역학의 이론에서 영감을 받았다고 한다. diffusion model은 이미지를 생성하는 것 외에도 이미지의 노이즈를 제거하거나 이미지의 빈 부분을 자연스럽게 채우는 등 다양한 기능과 결합될 수 있다.

 

0. Abstract

 

본 논문은 데이터셋의 확률분포를 추정하는 flexible하고 tractable한 확률 모델을 만들어냈다. 논문에서 제시한 diffusion model은 반복적인 diffusion process를 통해 데이터 구조를 천천히 붕괴시키고 이후 reverse process를 학습하여 데이터 구조를 복원한다.

 

1. Introduction

 

확률 모델에서 tractability와 flexibility는 상충관계이다.

Tractable Model : 모델을 이용한 계산이 어렵지 않다(해석적으로 해를 구할 수 있거나 쉽게 근사하여 구할 수 있다).

Flexible Model : 모델이 유연하여 데이터가 복잡하더라도 잘 부합할 수 있다.

 

# Example

$p(\mathbf{x})=\frac{\phi(\mathbf{x})}{Z}$

$\phi(\mathbf{x})$ : Any non-negative function

$Z$ : Normalization constant

 

위의 예시에서 확률 분포 $p(\mathbf{x})$는 flexible하지만 정규화 상수 $Z$를 계산하는 과정이 intractable하다.

 

diffusion model의 forward process(diffusion process)는 복잡한 데이터셋의 분포를 단순하고 다루기 쉬운 분포(정규분포)로 변환한다. 이 때 데이터 분포는 여러 단계에 걸쳐서 조금씩 변형된다. 각각의 단계에서는 Markov chain을 이용한다. 

 

어떠한 형태의 데이터셋에 대해서도 충분히 많은 diffusion process를 통해 단순한 분포의 데이터셋으로 변환할 수 있다. 따라서 diffusion model은 flexible하다.

 

reverse process에서는 단순하게 변환된 데이터 분포를 다시 여러 단계에 걸쳐 복원한다. 각각의 단계는 Markov chain으로 구성되며 forward process의 각 단계와 대응되어 이의 역과정을 학습한다.

 

reverse process의 각 단계는 forward process에서 진행된 '약간의' 변화만 학습하면 되므로 tractable하다. 따라서 전체 reverse process도 tractable하다.

 

이와 같은 forward, reverse process를 통해 tractable하고 flexible한 diffusion model을 구현할 수 있다.

 

2. Algorithm

2.1 Forward Trajectory

아래의 수식은 임의의 데이터 분포를 단순하고 tractable한 분포로 변환하는 forward process를 설명한다.

 

$q(\mathbf{x}^{(0)})$ : Data distribution

$\pi(\mathbf{y})$ : Well behaved (analytically tractable) distribution

$T_{\pi}\,({ \mathbf{y} | \mathbf{y} ^ {\prime} ; \beta })$ : Markov diffusion kernel

$\beta$ : Diffusion rate

 

$ \pi(\mathbf{y}) = \int{ d\mathbf{y}^{\prime}\, T_{\pi}\,({ \mathbf{y} |\mathbf{y} ^ {\prime} ; \beta }) \,\pi(\mathbf{y}^{\prime}) } $

 

$ q(\mathbf{x}^{(t)} |  \mathbf{x}^{(t-1)})  = T_{\pi}\, (\mathbf{x}^{(t)} |\mathbf{x}^{(t-1)} ; \beta_t) $

 

$ q(\mathbf{x} ^ {(0...T)} ) = q(\mathbf{x} ^ {(0)} ) \prod\limits_{t=1}^{T} q(\mathbf{x}^{(t)} |  \mathbf{x}^{(t-1)}) $ 

 

초기 데이터 분포 $ q(\mathbf{x} ^ {(0)}) $에 Markov diffusion kernel $q(\mathbf{x}^{(t)} |  \mathbf{x}^{(t-1)})$을 반복적으로 적용하여 tractable한 $\pi(\mathbf{x}^{(T)})$로 변환한다.

 

$ q(\mathbf{x}^{(t)} |  \mathbf{x}^{(t-1)})  = \mathcal{N} ( \mathbf{x} ^ {(t)} ; \mathbf{x} ^ {(t-1)} \sqrt{1-\beta_t} , \mathbf{I}\beta_t) $

 

본 논문에서 Markov diffusion kernel은 위와 같이 정규분포(혹은 이항분포)로 나타난다.

 

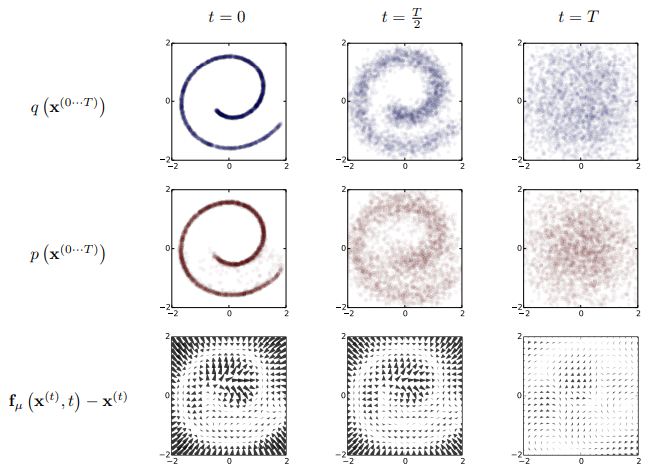
2.2 Reverse Trajectory

 

$ p(\mathbf{x}^{(T)}) = \pi(\mathbf{x}^{(T)}) $

 

$ p(\mathbf{x} ^ {(0...T)} ) = p(\mathbf{x} ^ {(0)} ) \prod\limits_{t=1}^{T} p(\mathbf{x}^{(t-1)} |  \mathbf{x}^{(t)}) $ 

 

충분히 작은 $\beta$에 대하여 정규분포 diffusion kernel의 reverse process는 forward process와 동일한 형태를 가진다는 것이 증명되어 있으므로 (Feller, 1949) $ q(\mathbf{x}^{(t)} |  \mathbf{x}^{(t-1)}) $의 역과정인 $ q(\mathbf{x}^{(t-1)} |  \mathbf{x}^{(t)}) $도 정규분포이다.

 

따라서 $ p(\mathbf{x}^{(t-1)} |  \mathbf{x}^{(t)})  $는 $ q(\mathbf{x}^{(t-1)} |  \mathbf{x}^{(t)})  $에 근사하도록 학습되며 학습 단계에서는 각 시점(t)별로 reverse kernel의 평균과 분산을 학습한다.

 

평균과 분산을 학습하기 위한 MLP 모델을 각각 만들어 모델이 해당 시점의 평균이나 분산을 추정하도록 학습시킨다.

 

위 그림은 t에 따른 데이터 분포 변화를 나타낸다. $f_\mu (\mathbf{x}^{(t)},t)$는 정규분포 $ q(\mathbf{x}^{(t-1)} ❘  \mathbf{x}^{(t)}) $의 평균을 추정하는 함수(MLP)이다.

 

2.3 Model Probability

 

모델이 생성하는 확률분포 $p(\mathbf{x}^{(0)})$는 아래와 같이 표현 가능하다.

 

$ p(\mathbf{x}^{(0)}) = \int{ d\mathbf{x}^{(1...T)} p(\mathbf{x}^{(0...T)}) } $

 

위의 intractable한 수식을 계산하기 위해 식을 변형한다.

 

$ p(\mathbf{x}^{(0)}) = \int{ d\mathbf{x}^{(1...T)} p(\mathbf{x}^{(0...T)}) \frac{q( \mathbf{x}^{(1...T)} | \mathbf{x}^{(0)})}{ q(\mathbf{x}^{(1...T)} |\mathbf{x}^{(0)}) } } $

 

$ = \int{ d\mathbf{x}^{(1...T)} q(\mathbf{x}^{(1...T)} |\mathbf{x}^{(0)}) \frac{ p(\mathbf{x}^{(0...T)}) }{ q(\mathbf{x}^{(1...T)} |\mathbf{x}^{(0)}) } } $

 

$ = \int{ d\mathbf{x}^{(1...T)}q(\mathbf{x}^{(1...T)} |\mathbf{x}^{(0)}) p(\mathbf{x}^{(T)}) \prod\limits_{t=1}^{T} \frac{p( \mathbf{x}^{(t-1)} | \mathbf{x}^{(t)} )} { q(\mathbf{x}^{(t)} |\mathbf{x}^{(t-1)} ) }  } $

 

마지막 수식은 forward trajectory $ q(\mathbf{x}^{1...T} | \mathbf{x}^{(0)}) $에서 샘플링한 값들을 평균하여 쉽게 구할 수 있다.

 

2.4 Training

 

Model의 log likelihood를 높이는 방향으로 train 시킨다. 이 때 $p(\mathbf{x}^{(0)})$가 $q(\mathbf{x}^{(0)})$

에 근접하도록 cross entropy를 계산한다.

 

$ L = \int{ d\mathbf{x}^{(0)} q(\mathbf{x}^{(0)}) \, log \,  p(\mathbf{x}^{(0)})  } $

 

$ = \int{ d\mathbf{x}^{(0)} q(\mathbf{x}^{(0)}) \, log \, \left[ \int{ d\mathbf{x}^{(1...T)}q(\mathbf{x}^{(1...T)} |\mathbf{x}^{(0)}) p(\mathbf{x}^{(T)}) \prod\limits_{t=1}^{T} \frac{p( \mathbf{x}^{(t-1)} | \mathbf{x}^{(t)} )} { q(\mathbf{x}^{(t)} |\mathbf{x}^{(t-1)} ) } } \right]  }  $

 

Jensen's inequality를 활용하면 아래와 같이 표현 가능하다. 자세한 유도 과정은 논문의 Appendix B에 설명되어 있다.

 

$L \geq K$

 

$ K = - \sum\limits_{t=2}^{T} \int{ d\mathbf{x}^{(0)} d\mathbf{x}^{(t)} q(\mathbf{x}^{(0)}, \mathbf{x}^{(t)}) D_{KL}( q( \mathbf{x}^{(t-1)} | \mathbf{x}^{(t)} , \mathbf{x}^{(0)} )  || p( \mathbf{x}^{(t-1)} | \mathbf{x}^{(t)} ) ) } + H_{q}(\mathbf{X}^{(T)}| (\mathbf{X}^{(0)} ) - H_{q}(\mathbf{X}^{(1)}|(\mathbf{X}^{(0)} ) - H_{p}(\mathbf{X}^{(T)}) $

 

이 때 Entropy와 KL divergence는 계산가능하므로 training은 L의 lower bound인 K를 최대화하는 방향으로 진행되며 이를 아래와 같이 표현할 수 있다.

 

$ \hat{p} (\mathbf{x}^{(t-1)} | \mathbf{x}^{(t)} ) = \underset{ p (\mathbf{x}^{(t-1)} |\mathbf{x}^{(t)} ) } {argmax}  K$

 

2.4.1 Setting the diffusion rate $\beta_t$

 

올바른 $\beta_t$의 설정은 모델의 성능 향상에 큰 도움이 된다. 본 논문에서는 과적합 방지를 위해 $\beta_1$을 직접 설정하고 $\beta_{2...T}$는 $K$에 대한 gradient ascent를 통해 값을 정한다. 하지만 후속 연구에서 $\beta_{t}$의 값을 사용하는 것이 효율적임이 확인되었다.

 

2.5 Multiplying Distributions, and Computing Posteriors

 

앞의 과정들을 통해 MLP가 $ q( \mathbf{x}^{(t-1)} | \mathbf{x}^{(t)} , \mathbf{x}^{(0)} ) $의 $\mu$와 $\sigma$를 추정하도록 만들고 이 값을 이용해 reverse process를 진행하면 초기 데이터 분포를 추정하는 확률 분포 $p(\mathbf{x} ^{(0)})$를 구할 수 있다. 학습이 잘 되었다면, 확률 분포 $p(\mathbf{x}^{(0)})$를 통해 초기 데이터와 유사한 형태를 갖는 데이터들을 생성할 수 있다.

 

만약 diffusion model이 signal denoising, inference of missing values 등의 추가적인 기능을 수행하도록 하기 위해서는 확률 분포 $p(\mathbf{x}^{(0)})$에 확률 분포 $r(\mathbf{x}^{(0)})$를 곱해서 구현할 수 있다. 이 때 확률 분포 $r(\mathbf{x}^{(0)})$는 특정 기능을 하는 bounded positive function이며 아래와 같이 나타난다.

 

$\tilde{p}(\mathbf{x}^{(0)}) \propto p(\mathbf{x}^{(0)}) \, r(\mathbf{x}^{(0)}) $

 

2.5.1 Modified Marginal Distributions

 

reverse process의 각 시점의 marginal distribution $p(\mathbf{x}^{(t)})$에 대해 이에 대응하는 함수 $r(\mathbf{x}^{(t)})$를 곱해준다.

 

$\tilde{p}(\mathbf{x}^{(t)}) =  \frac{1}{\tilde{Z}_t} p(\mathbf{x}^{(t)}) \, r(\mathbf{x}^{(t)}) $

 

$\tilde{Z}_t$ : Normalizing constant for the $t$th intermediate distirbution

 

2.5.2 Modified Diffusion Steps

 

Markov kernel $p(\mathbf{x}^{(t)} | \mathbf{x}^{t+1} )$은 아래의 평형 조건을 만족한다.

 

$ p(\mathbf{x}^{(t)}) = \int d\mathbf{x}^{(t+1)} p( \mathbf{x}^{(t)} | \mathbf{x}^{(t+1)}) p(\mathbf{x}^{(t+1)}) $

 

perturbed Markov kernel $ \tilde{p}(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)}) $도 위의 등식을 만족시켜야 한다.

 

$ \tilde{p}(\mathbf{x}^{(t)}) = \int d\mathbf{x}^{(t+1)} \tilde{p}( \mathbf{x}^{(t)} | \mathbf{x}^{(t+1)}) \tilde{p}(\mathbf{x}^{(t+1)}) $

 

$ \frac{p(\mathbf{x}^{(t)}) r(\mathbf{x}^{(t)})}{\tilde{Z}_t} = \int d\mathbf{x}^{(t+1)} \tilde{p}(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)}) \frac{p(\mathbf{x}^{(t+1)})r(\mathbf{x}^{(t+1)})}{\tilde{Z}_{t+1}} $

 

$ p(\mathbf{x}^{(t)}) = \int d\mathbf{x}^{(t+1)} \tilde{p}(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)}) \frac{\tilde{Z}_t r(\mathbf{x}^{(t+1)})}{\tilde{Z}_{t+1} r(\mathbf{x}^{(t)})} p(\mathbf{x}^{(t+1)}) $

 

아래의 등식이 성립한다면, 위의 등식도 성립한다.

 

$ \tilde{p}(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)}) = p(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)}) \frac{\tilde{Z}_{t+1}r(\mathbf{x}^{(t)})}{\tilde{Z}_{t}r(\mathbf{x}^{(t+1)})} $

 

$ \tilde{p}(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)}) $이 정규분포를 따르도록 식을 변형한다.

 

$ \tilde{p}(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)}) = \frac{1}{\tilde{Z}_{t}(\mathbf{x}^{(t+1)})} p(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)}) r(\mathbf{x}^{(t)}) $

$\tilde{Z}_{t}(\mathbf{x}^{(t+1)})$ : Normalization constant

 

이와 같은 식변형이 가능한 이유는 확률 분포 $p(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)})$가 작은 분산으로 인해 평균 주변에서 급격한 변화를 보이며 이로 인해 $ \frac{r(\mathbf{x}^{(t)})}{\mathbf{x}^{(t+1)}} $가 상대적으로 작은 perturbation으로 취급될 수 있기 때문이다.

 

2.5.3 Applying $r(\mathbf{x}^{(t)})$

 

2.5.2에서 설명한 바와 같이 $r(\mathbf{x}^{(t)})$는 정규분포 $p(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)})$과 비교했을 때 상대적으로 작은 perturbation으로 취급된다. 따라서 확률분포 $r(\mathbf{x}^{(t)})$는 정규분포의 평균에는 작은 영향을 끼치지만 분산에는 영향을 끼치지 못한다. 따라서 확률분포(정규분포) $\tilde{p}(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)})$은 $p(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)})$와 동일한 분포를 가지며, 약간 변화된 평균을 가진다. 이에 대한 자세한 설명은 논문의 Appendix C에 나와있다.

 

(a)는 원본 나무껍질 이미지이다. (b)는 (a)의 중앙 100 $\times$ 100 크기의 pixel들이 isotrophic Gaussian noise로 대체되었다. 이는 $\tilde{p}(\mathbf{x}^{(T)})$와 같다. (c)는 나무껍질 이미지들을 학습한 diffusion model을 이용해 중앙의 빈 구역을 채운 이미지이다.

 

위의 예시에서 확률 분포 $r(\mathbf{x}^{(0)})$는 중앙 100 $\times$ 100 pixel에서는 상수값을 갖고, 그 외의 구역에서는 delta function의 함수값을 가져 픽셀의 값을 유지하는 역할을 한다.

 

이와 같이 $r(\mathbf{x}^{(t)})$가 정규분포와 쉽게 곱해질 수 있는 형태의 확률 분포라면, $r(\mathbf{x}^{(t)})$는 reverse diffusion kernel $p(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)})$와 곱해져 inpainting, denosing 등의 다양한 기능을 수행할 수 있다.

 

2.5.4 Choosing $r(\mathbf{x}^{(t)})$

 

$r(\mathbf{x}^{(t)})$는 trajectory에 따라 천천히 변화하도록 설계하는 것이 일반적이다. 본 논문에서는 실험결과를 바탕으로 $r(\mathbf{x}^{(t)})$를 일정하게 유지한다.

 

$r(\mathbf{x}^{(t)}) = r(\mathbf{x}^{(0)})$

 

2.6 Entropy of Reverse Process

 

reverse trajectory 각 단계의 엔트로피 $H_{q}(\mathbf{X}^{(t-1)} | \mathbf{X}^{(t)})$의 상한과 하한을 아래와 같이 구할 수 있다.

 

$ H_{q}(\mathbf{X}^{(t)} | \mathbf{X}^{(t-1)}) + H_{q}(\mathbf{X}^{(t-1)} | \mathbf{X}^{(0)}) - H_{q}(\mathbf{X}^{(t)} | \mathbf{X}^{(0)}) \leq H_{q}(\mathbf{X}^{(t-1)} | \mathbf{X}^{(t)}) \leq H_{q}(\mathbf{X}^{(t)} | \mathbf{X}^{(t-1)}) $

 

유도과정은 논문의 Appendix A에 자세하게 설명되어 있다. 상한과 하한은 모두 forward process의 각 과정으로부터 쉽게 구할 수 있다.

 

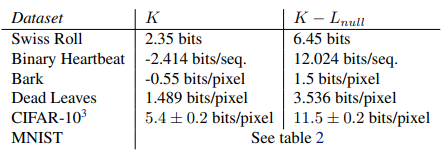
3. Experiments

 

본 논문에서는 diffusion model을 다양한 연속적인 데이터셋과 이진 데이터셋에 학습시켰다. gradient 계산에는 Theano 라이브러리가 사용되었다.

 

$K$는 log likelihood의 lower bound이고 $L_{null}$은 $\pi(\mathbf{x}^{(0)})$의 log likelihood이다. 즉 표의 오른쪽 열은 isotrophic Gaussian distribution과 비교하여 얼마나 개선되었는지를 나타낸다.

 

다른 알고리즘들과 log likelihood 값을 비교한 표이다.

 

4. Conclusion

 

본 논문은 diffusion model이라는, 확률 분포를 모델링하는 새로운 방법을 제시한다. 이 모델은 tractable(계산, 학습, 샘플링 과정이 쉬움)하면서 동시에 flexible(어떤 확률 분포든 학습 가능)한 특성을 갖고 있어. 기존의 생성형 모델들이 갖고 있었던 한계를 극복했다.