Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks는 2017년 ICML에서 발표된,
모델에 독립적인 meta learning 알고리즘을 제안한 논문입니다.
[MAML]
https://arxiv.org/abs/1703.03400
Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
We propose an algorithm for meta-learning that is model-agnostic, in the sense that it is compatible with any model trained with gradient descent and applicable to a variety of different learning problems, including classification, regression, and reinforc
arxiv.org
* Abstract
- 모델에 독립적인(gradient descent로 학습되는 어떤 모델에도 적용 가능한) meta learning 알고리즘을 제안
- 새로운 과제에서 소량의 데이터와 소수의 gradient step만으로도 좋은 일반화 성능을 낼 수 있도록 모델의 파라미터를 학습시키는 방식
- 두 가지 few-shot 이미지 분류 벤치마크에서 SOTA 달성, few-shot 회귀 문제에서 우수한 결과, 정책 그래디언트 기반 강화학습에서도 fine-tuning 속도 가속화
* Introduction
- 사람과 유사하게, 인공지능 에이전트도 적은 수의 예제만으로 빠르게 학습하고 적응할 수 있어야 함
- 이러한 빠르고 유연한 학습은 쉽지 않은데, 이는 소량의 새로운 정보와 기존의 경험을 통합하면서도 새로운 데이터에 과적합되지 않아야 하기 때문
- 또한, 기존 경험이나 새 데이터의 형태는 과제에 따라 다양하게 달라지므로, 최대한 범용적으로 적용하기 위해 meta-learning 메커니즘 역시 과제나 연산 방식에 구애받지 않아야 함
- MAML에서 제안하는 알고리즘은,
1. 학습 파라미터의 수를 늘리지 않으며,
2. 모델 아키텍처에 제약을 가하지 않고,
3. 완전 연결, 합성곱, 순환 신경망 등과도 쉽게 결합 가능하다.
4. 또한, 미분 불가능한 reinforcement learning objective와도 함께 사용될 수 있다.
* Model-Agnostic Meta-Learning
* Meta-Learning Problem Set-Up
- Few shot 메타러닝의 목표는, 소량의 데이터와 소수의 학습 iteration만으로도 새로운 과제에 빠르게 적응할 수 있는 모델을 학습하는 것
- 이를 위해 모델은 meta-learning phase에서 다양한 과제들을 통해 학습됨 (개별 task 자체가 학습의 단위)
- 각 task T

- L: Loss function
- q(x_1): 초기 관측값 분포
- q(x_t+1 | x_t, a_t): 상태 전이 분포
- H: 에피소드 길이
- meta learning의 흐름
1. task T_i를 p(T)에서 sampling
2. 모델은 해당 task T_i에서 추출된 K개의 샘플과 손실 L_{T_i}를 사용해 학습
3. 이후, 같은 task T_i의 새로운 샘플들에 대해 성능 평가
4. 이때의 test error가 메타러닝 과정에서의 training error로 사용됨
5. 이를 바탕으로 모델 f의 파라미터 개선
- 이러한 과정을 반복하며, 메타학습이 끝나면 p(T)로부터 새로운 task들을 샘플링하여, K개의 샘플만으로 얼마나 잘 학습하는지를 통해 meta-performance를 평가
* A Model-Agnostic Meta-Learning Algorithm
- 핵심 직관: 어떤 내부 표현은 다른 것보다 더 전이 가능하다 → 범용적인 내부 표현이 존재한다
- 목표: 모델을 학습할 때 gradient 기반 학습이 task 분포 p(T)로부터 샘플링된 새로운 task들에 대해 빠르게 수렴하도록 만드는 것
- Objective function

- Algorithm

- gradient update가 gradient를 통해 또 다른 gradient를 계산하는 구조 → f를 통해 한 번 더 backward pass 수행해야 함 → Hessian-vector product 계산
* Species of MAML
* Supervised Regression and Classification
- horizon H = 1
- x_t 생략 (모델이 단일 입려을 받아 단일 출력을 생성하므로)
- task T_i는 분포 q_i로부터 독립적으로 샘플링된 K개의 관측값 x를 생성하고, 손실은 모델의 출력과 해당 관측값에 대한 정답 y 사이의 오차로 정의 (회귀: MSE, 분류: CE)
- MSE

- CE

- Algorithm

* Reinforcement Learning
- task 전체는 수평 길이 H를 가진 MDP
- 학습자는 소수의 trajectory만 관측 가능
- 학습 대상 모델 f_theta는 policy이며, 각 시점 t에서 상태 x_t를 입력받아 행동 a_t의 확률 분포를 출력
- Loss function: 총 기대보상의 음수
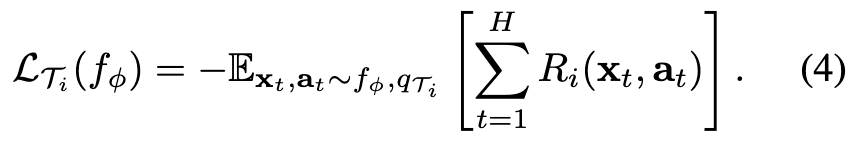
- 각 task T_i에 대해 정책 f_theta로부터 K개의 rollout을 수집 → 이에 대한 보상 R(x_t, a_T)도 함께 수집하여 새로운 task에 대한 적응에 사용
- Algorithm

- 기대 보상은 보통 non-differentiable → policy gradient 기법 사용
- on-policy 알고리즘 → f_theta 를 적응시키는 동안 추가적인 gradient step마다 새 샘플 필요
- 구조는 알고리즘 2와 동일하되, 5번과 8번 단계에서 task T_i의 환경에서 새로운 trajectory를 sampling
* Experimental Evaluation
- 실험 평가의 목적
1. MAML이 새로운 task에 대해 빠르게 학습하도록 만들 수 있는가?
2. MAML은 지도 회귀, 분류, 강화학습을 포함한 여러 다양한 도메인에서 메타러닝에 사용될 수 있는가?
3. MAML로 학습된 모델이 추가적인 gradient 업데이트나 예시들을 통해 계속 성능이 향상될 수 있는가?
* Regression
- 각 task는 사인(sine) 함수를 대상으로 입력으로부터 출력을 회귀하는 문제이며, task마다 amplitude와 phase가 달라진다.
- Baseline
(a) 모든 태스크에 대해 pretraining한 후, test 시점에서 gradient descent로 fine-tuning
(b) 진짜 진폭과 위상 정보를 입력으로 받는 oracle
- Results

* Classification
- Vinyals et al. (2016)이 제안한 실험 프로토콜을 따름 → 1-shot 또는 5-shot으로 N-way 분류를 빠르게 학습
- N-way 분류 문제:
1. N개의 보지 못한 클래스들을 선택하고,
2. 각 클래스마다 K개의 예시를 모델에 제공한 뒤,
3. 모델이 해당 N개의 클래스 중에서 새로운 샘플을 정확히 분류할 수 있는지 평가
- Omniglot, Minilmagenet 데이터셋 사용
- Results

* Reinforcement Learning
- rllab 벤치마크 모음집의 시뮬레이션 연속 제어 환경을 기반으로 여러 개의 task set 구성
- Baseline
(a) 모든 task를 기반으로 하나의 정책을 pretraining한 후 fine-tuning
(b) 무작위로 초기화된 정책을 학습하는 방식
(c) oracle
- 2D Navigation, Locomotion





