Introduction
neural network 훈련은 매우 복잡하고 non-convex한 함수의 최소를 찾는 과정이다.
- 훈련 parameter를 잘 설정하거나, optimizer를 잘 사용해 global minimum을 쉽게 구할 수 도 있지만 이론보다는 실제 코드 실행으로 결과를 얻어내는 딥러닝의 특성상 이는 매우 불확실한 알고리즘. → 우리는 더 확실하게 loss를 구할 수 있는 이론적 배경이 필요하다.
- 본 논문에서는 더 쉽게 loss를 구할 수 있는 방법으로 주어진 함수의 ‘시각화’가 선행되어야 한다고 주장. → 주어진 loss에서 서로 다른 network의 선택이 최소화하는 과정, loss landscape에 어떠한 영향을 주는지 평가하고자 함.
Contributions
- 일반적인 시각화 방법으로는 복잡한 loss 함수의 개형을 파악하기 어려웠다.
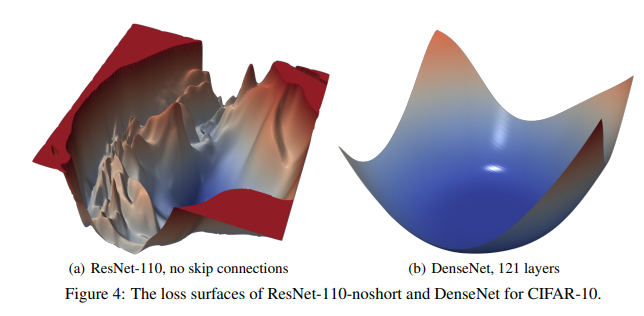
- neural network가 깊어진다면, loss landscape 함수 역시 다양한 연산으로 인해 매우 복잡한 형태로 바뀌게 된다.
- ResNet에서 사용하는 Skip Connection을 이용 시 loss 함수가 간단해진다.

- Non-convexity는 local minima 주위 Hessian의 eigenvalue를 계산함으로서 측정이 가능하다.
- SGD를 사용하였고, 고차원의 loss 함수를 매우 낮은 차원으로 낮추었을 때 해당 함수의 증감, 오목 볼록성등의 측정이 용이해졌다. → PCA 등의 차원 축소 기법을 이용함
- trajectory(궤도) : 에이전트가 지나온 일련의 상태와 행동을 trajectory라고도 한다.
Thoretical Background
많은 이론 지식들은 특정한 loss 함수에 대한 최적화된 방법을 제시할 뿐이었다.
- loss 함수의 flatness/sharpness를 정확히 판단할 수 있으면 결과를 구하기 쉽다.
- eigenvalue와 Hessian을 이용해 loss 함수의 convexity를 구할 수 있다.
- loss 함수의 sharpness를 local entropy를 이용해 구할 수 있다.
Loss Function Visualization
1차원의 점을 움직이며 설명하지만, 많은 parameter를 표현하는 데에 1차원은 적합하지 않았다. 3차원 이상의 그래프를 그렸을 때, 1차원일 때는 발견되지 않았던 non-convexity에 대한 측정이 가능해졌다./
f(α,β)=L(θ∗+αδ+βη)
말 그대로 함수 위에서 움직이는 점들을 묘사한 것. θ∗가 local minimum이며, α,β=0 일 때 local minumum에 도착하게 된다.
Filter-Wise Normalization
일반적인 시각화, normalization 방식으로는 그래프의 특성을 파악하기 어려웠다.
- Gaussian으로 정규화를 수행 시 모든 크기가 1 내에서 이루어지기 때문에 그래프에서는 시각적인 왜곡이 발생(Scale Invariance)
- Batch normalization을 수행하면 이 현상이 더 심해짐
- 더 좋은 loss 함수를 위한 네트워크를 정하는 것이 목표이기 때문에 일반적인 딥러닝 기법이 아닌 다른 방법이 필요하였다. → Filter-wise normalization
di,j=di,j∣∣di,j∣∣∣∣θi,j∣∣
각 벡터를 크기로 나눠준 후 local minimum의 크기와 같은 벡터를 만들어 parameter로 사용한다. → 중요한 그래프 지점의 특성들을 나타내는 데 이러한 방식이 더 결과가 좋았음 → 신경망 i번째 layer의 j번째 filter를 사용 시의 parameter들을 표현한 d
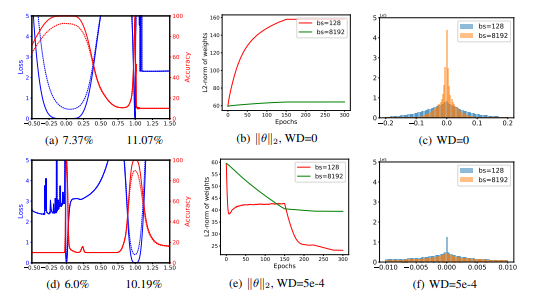
Sharp vs Flat
그래프를 그렸을 때 Sharp한 형태의 그래프가 더 minimum을 찾는데에 효과적이더라..(당연??)
- batch의 크기가 커질수록 그래프의 sharpness가 커진다. SGD같은 느린 optimizer를 이용하면 그래프가 flat해진다. ⇒ sharp한 그래프는 초기에는 잘 내려가지만, local, global minimum 근처에서는 그래프가 오히려 flat해지는 문제가 생겼다. → 적절한 네트워크 선택이 중요할 듯..
- 가장 Sharp해지는 결과는 ResNet-56을 사용하였을 때!!