[2025-1] 이재호 - 3D Gaussian Splatting for Real-Time Radiance Field Rendering

https://arxiv.org/pdf/2308.04079 - Bernhard Kerbl, Georgios Kopanas, Thomas Leimkuhler, George Drettakis

Abstract

기존 Radiance Field (NeRF) 기반 방법은 고화질 뷰 합성은 가능하지만, 느리고 무거운 학습 비용과 실시간 렌더링 불가라는 한계가 있음.
본 논문은 1080p 해상도에서 30fps 이상의 실시간 렌더링과 SOTA 수준의 화질을 동시에 달성하기 위해 다음 세 가지 핵심 요소를 도입:

3D Gaussian Representation
- 카메라 캘리브레이션으로 얻은 sparse point로 초기화
- 불필요한 빈 공간의 계산을 줄이고 연속적인 radiance field의 장점을 유지
Interleaved Optimization & Density Control
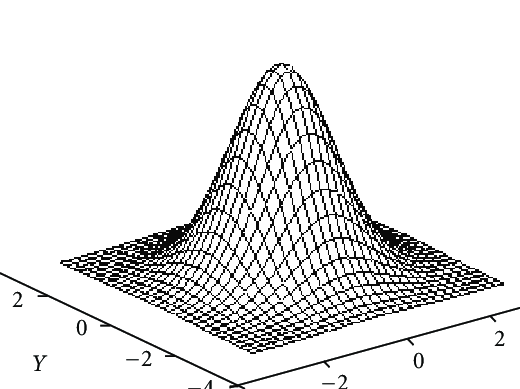
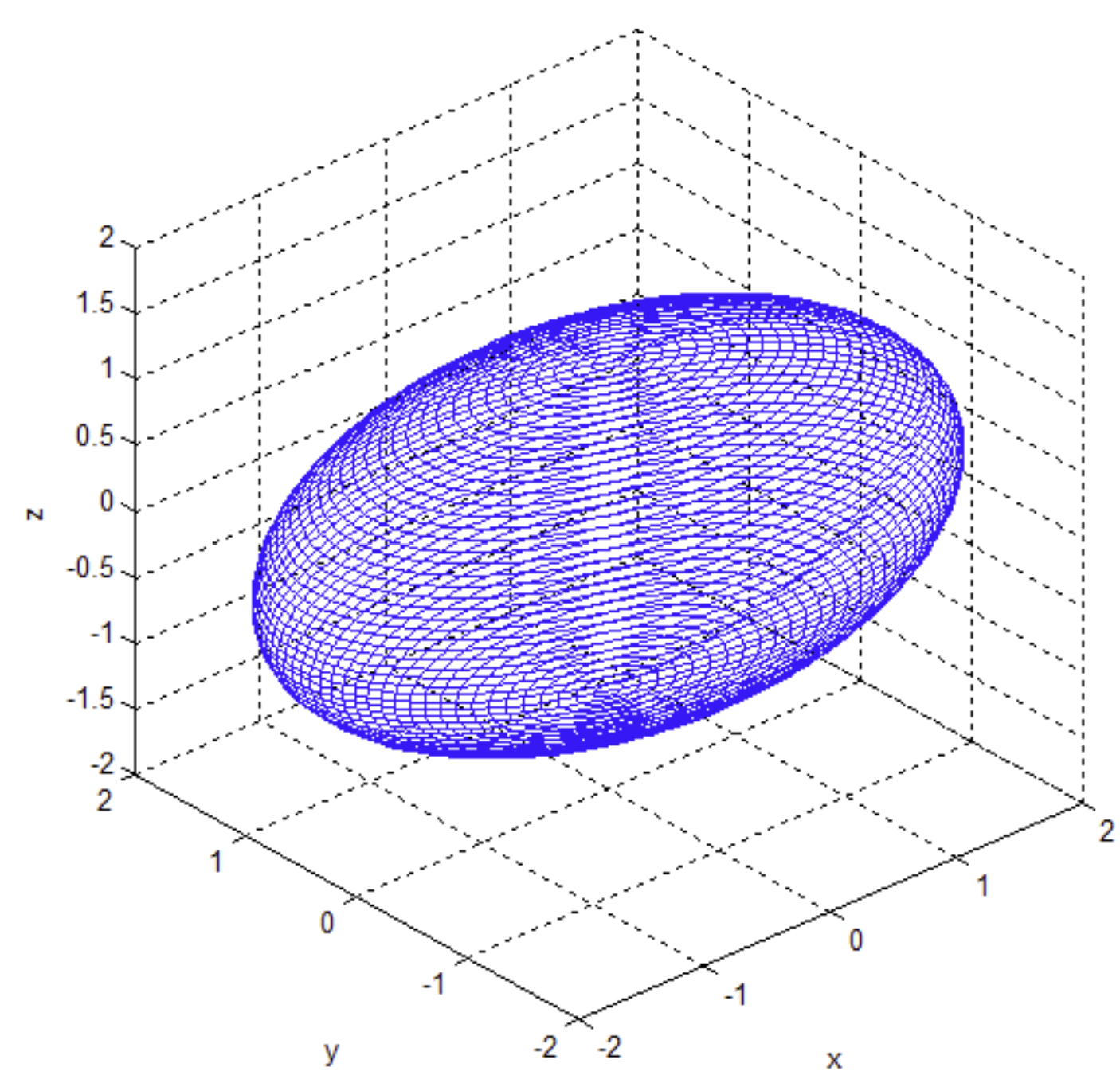
- 공분산 최적화 (anisotropic covariance)
- 필요에 따라 Gaussian을 추가/삭제하여 장면을 정확하게 표현
Fast Visibility-Aware Rendering
- Visibility-aware anisotropic splatting
- 학습과 렌더링을 동시에 가속화 → 실시간 렌더링 가능

이 방법을 통해 기존 방법들보다 더 빠르고 효율적으로 고화질의 새로운 시점 뷰를 생성할 수 있음을 다양한 데이터셋에서 검증.

1. Introduction

문제점

기존 NeRF 계열 방법은 고화질 novel view synthesis가 가능하지만, 렌더링 속도가 느림 (주로 MLP와 ray marching 사용).
속도를 높인 방법들은 품질이 떨어지거나 실시간으로 렌더링 불가능.
특히 unbounded scenes와 1080p 고해상도 환경에서는 real-time 렌더링이 어려움.

해결 방법 (3가지 핵심 요소)

3D Gaussian Representation 도입
- 기존 NeRF처럼 연속적 표현이 가능하면서도, 포인트 기반 구조로 효율적.
- SfM(SfM으로 얻은 sparse point cloud)으로 초기화 후, 3D Gaussian으로 scene을 표현.
- Differentiable volumetric representation과 효율적인 rasterization을 동시에 가짐.
3D Gaussian의 속성 최적화
- Gaussian의 3D 위치, 불투명도(α), 비등방성 공분산(anisotropic covariance), SH(spherical harmonic) 계수를 최적화.
- adaptive density control 기법과 병행하여 Gaussians의 수를 동적으로 조절.
Tile-based fast rasterization
- GPU 친화적인 tile-based splatting을 이용해 실시간 렌더링.
- visibility ordering을 고려한 anisotropic splatting을 통해 빠르고 정확한 backward pass 가능.

기여 (Contributions)

비등방성 3D Gaussian을 이용해 고품질, unstructured radiance field 표현 제안.
adaptive density control과 interleaved optimization을 통한 효율적 최적화.
GPU friendly한 real-time rendering 달성 (SOTA 수준의 품질, ≥ 30fps, 1080p).

2. Related works

2.1 Traditional Scene Reconstruction and Rendering

초기 novel-view synthesis 방법은 light field 기반 → dense하게 샘플링 필요
Structure-from-Motion (SfM) → sparse point cloud를 추정하여 multi-view로 3D scene 복원
이후 Multi-View Stereo (MVS) → full 3D reconstruction 가능
이런 방식들은 geometry에 의존 → geometry가 없는 부분은 복원 어려움 & 과도한 재구성(Over-reconstruction) 문제
Neural rendering 방법들이 등장하며 기존 방식보다 artifact 감소 & 효율적 메모리 사용

2.2 Neural Rendering and Radiance Fields

초기 neural rendering은 CNN 기반으로 novel-view synthesis 진행 → geometry 기반 제한성
Volumetric radiance fields (NeRF 등) → continuous differentiable density field를 사용
NeRF의 장점:
- 고품질 view synthesis 가능
- importance sampling, positional encoding으로 품질 향상
단점:
- MLP 사용 → 매우 느림 (training, rendering cost ↑)
- stochastic sampling 필요 → 시간 소모 & 노이즈 발생
최근 방법들은 fast training & rendering을 위해 spatial data structure (voxel, hash grid 등) 사용
- 하지만 여전히 high-res rendering에 한계
- 대부분 volumetric ray-marching 사용 → 실시간 불가능

2.3 Point-Based Rendering and Radiance Fields

Point-based rendering:
- 명시적 point 표현 사용 → unstructured
- fast GPU rasterization에 적합, 그러나 discontinuity & hole 문제
최근 differentiable point-based rendering:
- CNN 활용하여 novel view synthesis 가능
- MVS 의존성 여전
NeRF와 비교:
- NeRF는 volumetric & continuous → random sampling 필요
- Point-based는 unstructured explicit representation → fast but detail 부족
Gaussian Splatting:
- Point-based rendering에 volumetric radiance field 개념을 결합
- Gaussian α-blending & visibility ordering 사용 → high quality + real-time rendering 가능

Overview

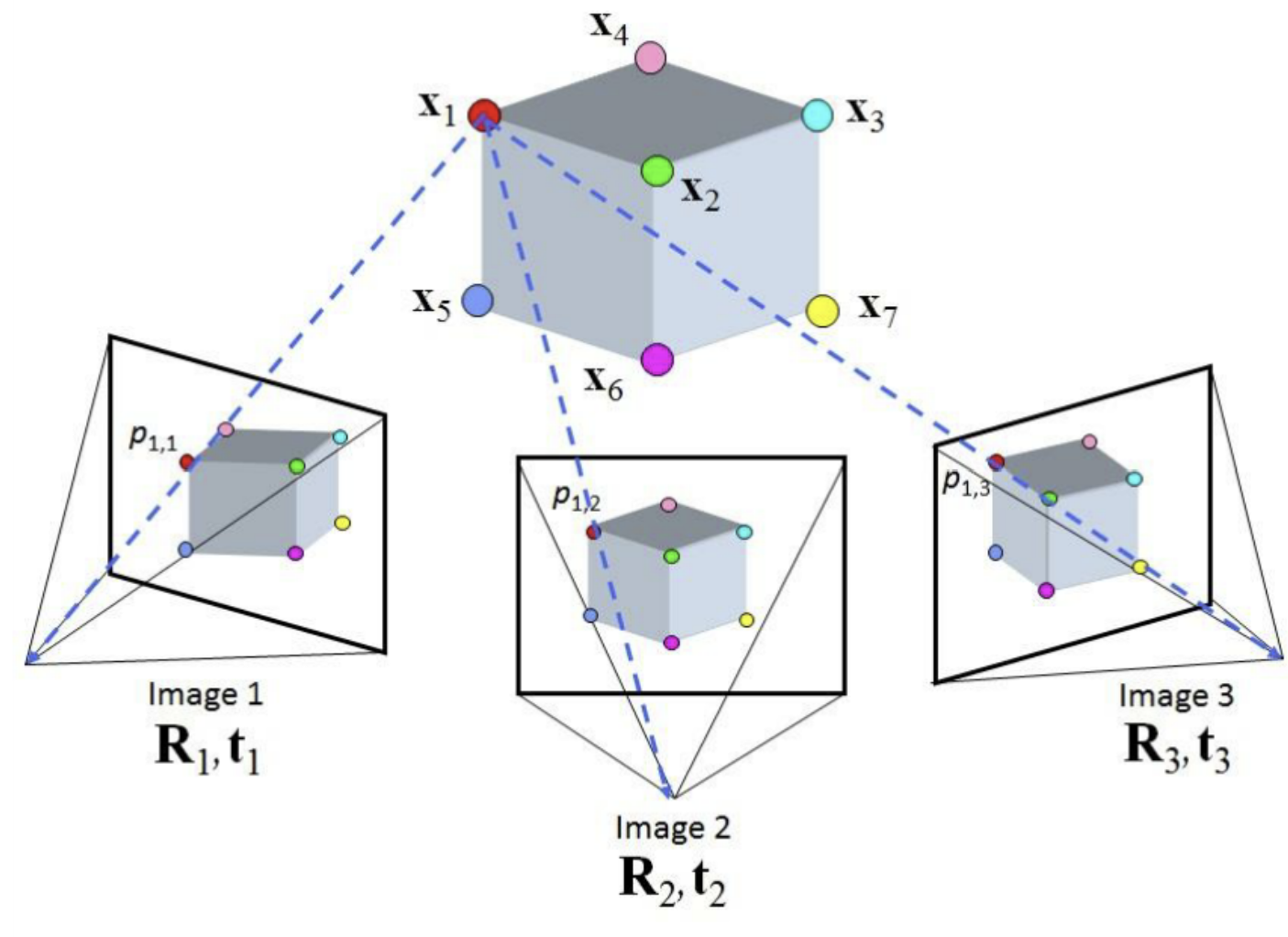
입력: 여러 장의 static scene 이미지를 SfM(Structure-from-Motion)을 통해 camera calibration → sparse point cloud 획득
이 point cloud로부터 3D Gaussians 생성 (각 Gaussian은 position, covariance, opacity α로 정의)
Anisotropic volumetric splats 사용 → fine structure를 compact하게 표현 가능
Radiance field의 색 정보는 Spherical Harmonics (SH)로 표현
전체 과정:
- 3D Gaussian의 position, covariance, α, SH coefficient를 반복적으로 최적화
- 중간에 adaptive density control 수행 (필요시 Gaussian 추가/제거)
핵심 효율성:
- Tile-based rasterizer 사용 → anisotropic splats를 빠르고 정확하게 α-blending하여 visibility 보장
- Fast backward pass 가능 (α 누적값 추적) → gradient 받을 Gaussian 개수 제한 없음

4. Differentiable 3D Gaussian Splatting

목표: SfM에서 얻은 sparse point cloud로부터 normals 없이 고품질의 새로운 뷰를 생성하는 장면 표현 최적화.
왜 Normal을 사용하지 않는가?
- 기존 point-based 방법은 각 포인트의 normal (법선벡터) 을 이용해 평면적으로 해석했지만, SfM 포인트는 너무 희소해서 normals 추정이 어렵고, noisy.
- 따라서 법선 추정 없이 사용할 수 있는 3D Gaussian 을 사용.
3D Gaussian 사용 이유
- 연속적인 volumetric 표현의 특성을 가지면서, 구조화되지 않고(explicit), 빠른 렌더링 가능.
- 2D splat으로 쉽게 투영 가능하고, α-blending으로 빠르게 렌더링 가능.
3D Gaussian 정의
- 위치(μ), 전체 3D covariance matrix Σ, 불투명도 α로 표현.
- Σ는 물리적으로 positive semi-definite (양의 준정부호) 이어야 함 → 일반적인 gradient descent로는 최적화 과정에서 유효한 covariance를 유지하기 어려움.

Gaussian defined with Covariance Matrix in world space

World space covariance matrix를 camera coordinates의 covariance matrix로 변환

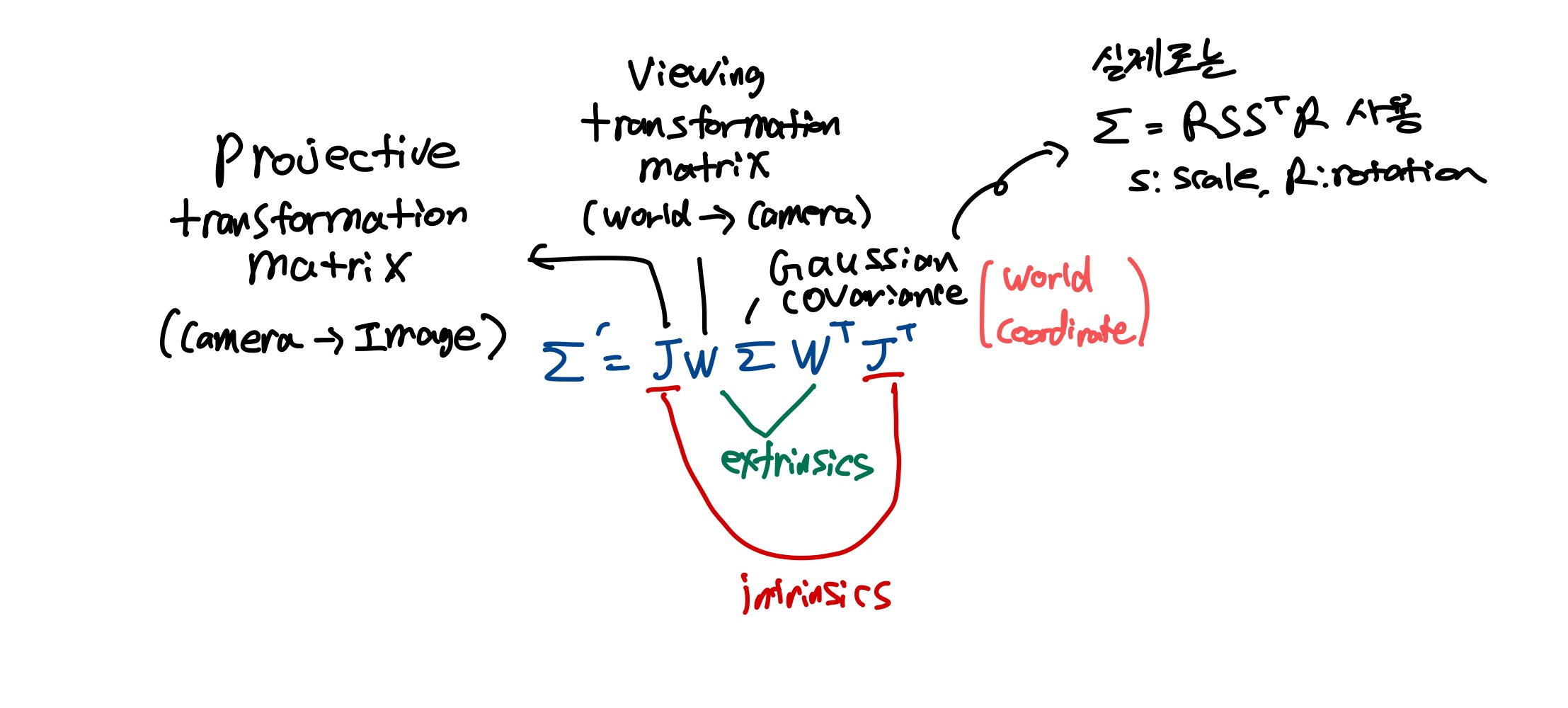
대신, 직관적이고 효율적인 표현 방식 사용
- Scaling matrix S (크기 조절)와 Rotation matrix R (회전)을 이용해 Σ 표현.
  - Σ = R S Sᵀ Rᵀ
    - 파라미터 최적화 시 scaling vector s와 quaternion q로 저장해 독립적으로 최적화.

최종적으로
- 다양한 형태의 geometry에 잘 적응할 수 있도록 anisotropic covariance 를 학습.
- 이는 captured scene을 상대적으로 compact하게 표현 가능하게 함.

5. Adaptive Density Control of 3D Gaussians

핵심은 3D Gaussian 파라미터 최적화를 통해 free-view novel view synthesis가 가능하도록 장면을 정확히 표현하는 것.
최적화하는 파라미터:
- 위치 (p)
- opacity (α)
- 공분산 행렬 (Σ)
- Spherical Harmonics (SH) 계수 → 각 Gaussian의 색상 (c) 표현
이 최적화 과정은 Gaussian 밀도 제어 (adaptive density control) 단계와 번갈아 수행됨.
- 필요 시 Gaussian을 추가하거나 제거하여 장면을 더 잘 표현할 수 있도록 함.

5.1 Optimization

최적화 과정
3D Gaussian들의 위치, α(불투명도), 공분산 Σ, SH 계수(색상)를 최적화하여 장면을 정확히 재구성하고 free-view synthesis가 가능하도록 함. 최적화 과정은 반복적으로 렌더링 결과와 ground-truth 이미지를 비교하면서 진행됨.
Geometry 오류 수정 3D-2D 프로젝션의 모호성 때문에 geometry가 잘못 배치될 수 있으므로 geometry를 새로 만들거나 (create), 제거하거나 (destroy), 이동 (move)하는 과정이 필요.
Compact Representation Large homogeneous areas는 소수의 큰 anisotropic Gaussian으로 표현되기 때문에 compact한 표현을 위해 covariance의 품질이 중요.
최적화 방법
- Stochastic Gradient Descent (SGD) 사용
- CUDA 가속 및 custom kernel을 활용하여 효율적으로 최적화 수행
- Fast rasterization 알고리즘을 사용하여 최적화의 computational bottleneck을 해결
활성화 함수
- α 값은 [0, 1] 범위로 제한하기 위해 sigmoid 함수 사용
- 공분산 크기(scale)는 exponential activation 사용
초기화
- 공분산 행렬은 초기 isotropic Gaussian으로 설정 (가장 가까운 3개 포인트의 거리 평균 기반)
- 위치는 exponential decay schedule로 업데이트
- L1 loss 와 D-SSIM (Structural Similarity) 의 가중합 사용
- λ = 0.2 사용Loss Function

5.2 Adaptive Control of Gaussians

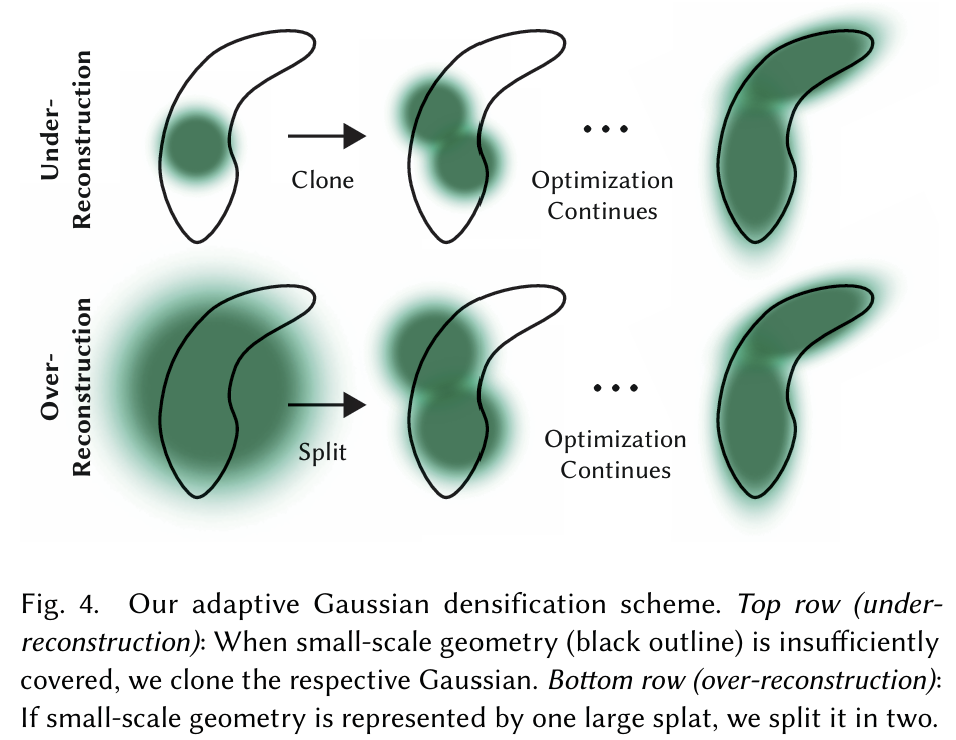
필요성
초기 SfM 포인트는 sparse하기 때문에, 단순히 Gaussian들의 위치와 크기만 최적화하면 fine details를 담기 어려움.
→ 따라서 adaptive하게 Gaussian의 수와 밀도를 조절하는 과정이 필요.
방식
- Densification (추가)
  새 Gaussian 추가: 특정 영역에서 geometry와 appearance의 복잡도가 높으면 새 Gaussians를 추가해 세밀하게 표현.
  - 주로 학습 초기에 많이 추가됨.
- Pruning (제거)
  불필요한 Gaussian 삭제: 투명도가 낮거나 기여도가 낮은 Gaussian을 제거하여 연산 효율성 확보.
  - 주로 학습 후반에 많이 제거됨.
Trigger 조건
- 일정 에폭마다, 또는 최적화 과정에서 특정 조건 만족 시 자동으로 추가/삭제 수행.
- 주로 렌더링된 이미지와 GT 이미지의 차이를 기반으로 판단.
장점
- 복잡한 영역은 더 촘촘하게, 단순한 영역은 더 sparsely 표현 가능.
- 최적화된 Gaussians의 수를 1~5 million 범위 내로 유지 가능
- 컴팩트하고 효율적인 표현을 달성할 수 있음.

6. Fast Differentiable Rasterizer for Gaussians

1) 타일 기반 정렬 (Tile-Based Sorting)

화면을 16×16 tiles로 나눔.
View frustum (카메라의 시야 영역)과 비교해 99% confidence interval 내에 위치하는 Gaussian만 남기고, 나머지는 버림.
Near plane에 너무 가까운 Gaussians와 Frustum 밖에 있는 Gaussians은 projection 불안정성 때문에 제거.
각 Gaussian이 overlap하는 tile들의 리스트를 만들고, tile ID + depth를 기준으로 Radix sort를 통해 sorting.

2) Forward pass에서 α-blending

정렬된 리스트를 따라 front-to-back으로 Gaussian의 α 값을 누적하며 blending.
α가 1에 도달하면 해당 pixel에 대한 blending은 중지.
이전 방법들보다 더 많은 blended Gaussians를 허용해 복잡한 씬에서도 성능 저하 없이 수행 가능.

3) Backward pass에서 gradient 계산

Forward pass에서 사용된 tile 리스트와 정렬된 Gaussians를 그대로 재사용해 back-to-front로 traversal.
Forward pass에서 최종 α 값을 저장해두고 backward 시 사용.
각 point의 α로 나눠주어 gradient 계산 시 필요한 coefficient를 얻음.
메모리 효율을 위해 forward pass에서 blended된 point의 full sequence를 저장하지 않고 traversal로 대체.

# Algorithm

7.1 Implementation

구현
- Python + PyTorch로 구현.
- Rasterization은 기존 방법을 확장하여 custom CUDA kernel로 작성.
- Fast sorting을 위해 NVIDIA CUB의 Radix sort 사용.
- 결과 확인을 위해 SIBR interactive viewer 사용.
Optimization Details
- Stability 확보를 위해 low resolution에서 warm-up 후 high resolution으로 업샘플링:
  - 초기에는 해상도를 4배 낮춰서 250~500회 iteration 진행.
  - 이후 2배 업샘플링, 다시 250~500회 iteration.
- SH coefficient optimization의 어려움:
  - 시야각 정보 부족 시 (ex. 장면 한쪽 모서리 촬영, inside-out capture) SH의 zero-order component (diffuse color)가 왜곡됨.
  - 이를 방지하기 위해 초기에는 zero-order component만 최적화하고, 이후 1000 iteration마다 SH의 band를 하나씩 추가하여 최종적으로 4 bands 사용.

7.2 Results and Evaluation

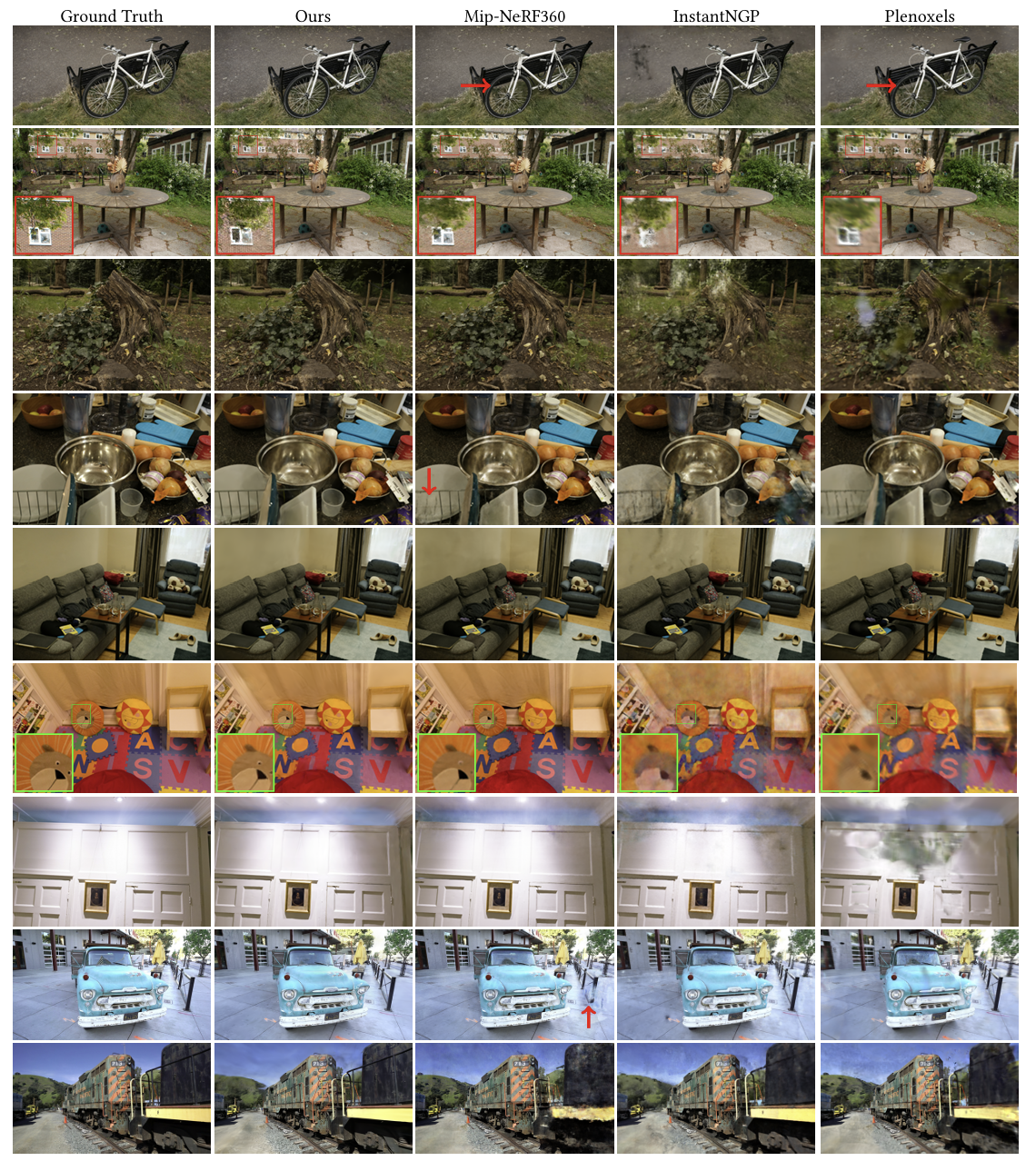
전체 평가

총 13개의 실제 장면과 Blender synthetic dataset을 사용하여 평가.
주요 비교 대상:
- Mip-NeRF360 (최신 SOTA NeRF 렌더링 품질)
- 빠른 NeRF 방법들: InstantNGP, Plenoxels
동일한 하이퍼파라미터 설정으로 모든 실험 진행.

실제 장면 (Real-World Scenes)

품질: Mip-NeRF360과 동등하거나 약간 더 좋은 품질.
학습 시간:
- Mip-NeRF360: 48시간
- 제안 방법: 35~45분
- 렌더링 속도: 10초/프레임
빠른 NeRF 방법 (InstantNGP, Plenoxels) 대비:
- 초반 5~10분만으로도 이들과 비슷한 품질.
- 추가 학습을 통해 SOTA 품질까지 도달 (빠른 NeRF 방법은 추가 학습해도 품질 한계 있음).
특이점:
- 기존 방법들은 먼 거리에서 세부 정보가 깨짐.
- 제안 방법은 먼 거리에서도 고해상도 세부 정보 유지.

Synthetic Bounded Scenes (Blender Dataset)

초기화: 10만 개의 랜덤 Gaussian으로 시작.
최종 학습 후:
- 6천~1만 개 meaningful Gaussians으로 pruning.
- PSNR 측정 기준으로 기존 방법과 SOTA 품질 도달.
- 모델 compactness: 최종 모델 크기 200k~500k Gaussians/scene.

Compactness (모델 크기)

기존 explicit scene representation (Zhang et al. 2022) 대비:
- 1/4의 파라미터 수로 동일 PSNR 품질 달성.
- 평균 모델 크기: 3.8MB (기존 방법: 9MB)
- 단, SH 계수는 두 차수(degrees)만 사용 (기존과 동일 조건).

7.3 Ablation Study

1. Initialization from SfM

기본적으로 Structure-from-Motion (SfM)에서 얻은 sparse point cloud를 초기화로 사용.
이를 사용하지 않고 랜덤 초기화하면:
- 성능은 크게 떨어지지 않지만, 특히 background에서 품질 저하가 발생.
- 더 많은 floaters (실제 geometry에 대응하지 않는 쓸모없는 Gaussian들) 발생.
- NeRF synthetic dataset에서는 background가 없기 때문에 이 영향이 없음.

2. Densification

Gaussian을 추가하거나 나누는 Clone & Split 전략을 평가.
Split을 비활성화하면 background 재구성 품질이 떨어짐.
Clone을 비활성화하면 가느다란 구조 표현에 어려움.
두 방법 모두 빠르고 좋은 수렴을 위해 중요.

3. Unlimited depth complexity of splats with gradients

기존 방법은 특정 depth 이후 splat들에 대해 gradient 계산을 제한했지만,
본 논문에서는 제한을 두지 않고 모든 splat에 대해 gradient 업데이트 가능.
실험적으로 제한을 두면 학습 품질이 크게 저하되고 (PSNR -11dB), 최적화가 불안정해짐.

4. Anisotropic Covariance

Gaussian의 공분산을 단일 scalar로 제한하는 경우와, full anisotropic covariance를 사용하는 경우를 비교.
Full covariance 사용 시 geometry에 더 잘 align되고, 더 적은 수의 Gaussians으로 더 높은 품질의 렌더링 가능.

5. Spherical Harmonics

SH (Spherical Harmonics)를 사용하여 view-dependent appearance 표현.
SH를 제거하면 PSNR 성능이 감소.
SH는 관측 방향에 따라 색상이 달라지는 효과를 잘 표현하기 위해 필요.

7.4 Limitations

1. 관찰 부족 영역에서의 문제

장면(scene)을 충분히 관찰하지 못한 영역에서는 artifact(잡음, 이상현상)이 발생함.
이는 Mip-NeRF360 같은 다른 최신 방법들도 겪는 문제로, 이 논문만의 한계는 아님.
특히 anisotropic Gaussians가 장점도 있지만, 잘못 최적화되면 늘어진(splotchy) 형태의 Gaussian이 생길 수 있음.

2. Popping artifacts

최적화 중 큰 Gaussian이 생성되면 시점에 따라 갑작스럽게 보이거나 사라지는 (popping) 문제가 생김.
이유:
- 단순한 guard band 기반 rejection: tile 밖에 위치한 Gaussian을 무조건 제거.
- simple visibility algorithm: Gaussian의 깊이 정렬 순서가 갑자기 바뀌는 문제 발생 → blending 순서 변경.
해결 방향: 더 정교한 culling/visibility 알고리즘 또는 anti-aliasing 기법 필요.
현재는 regularization 적용이 없어 이러한 문제를 완화하기 어려움.

3. 대규모 장면 학습의 어려움

모든 실험에 동일한 하이퍼파라미터 사용했으나, **복잡한 도시 장면(urban scenes)**에서는 position learning rate를 낮춰야 수렴이 잘 됨.
즉, 복잡한 장면에 대한 일반화 어려움이 있음.

4. 높은 메모리 소비

기존 포인트 기반 방법보다 메모리 효율은 높지만,
NeRF 기반 방식보다 GPU 메모리 사용량이 훨씬 많음 (최대 20GB까지 사용).
특히 훈련 중엔 많은 메모리 소비, 추론 중에도 수백 MB~GB 단위의 메모리 필요.
타일 기반 rasterizer만 해도 30~500MB 정도 필요함.

💡 개선 방향 제안

더 정교한 구현으로 메모리 최적화 가능 (예: InstantNGP 방식처럼).
압축 기법 (e.g. point cloud compression) 적용 가능성도 제시됨.