[2025-1] 이재호 Titans: Learning to Memorize at Test Time

https://arxiv.org/abs/2501.00663

Ali Behrouz, Peilin Zhong, and Vahab Mirrokni - Google Research 

Titans: Learning to Memorize at Test Time

 

Abstract

• 기존의 RNN 모델들은 데이터를 고정된 크기로 압축해 사용하고 Attention 기반 모델은 문맥을 더 정확히 파악하지만 높은 연산 비용이 듦
• Titans는 Neural memory module을 활용하여 장기 기억을 유지하면서도 빠른 병렬 병렬 학습이 가능한 새로운 아키텍처를 제안하며 이를 효과적으로 통합하기 위한 세 가지 변형(variants)을 제안함
• 실험 결과, Titans는 Transformers나 recent modern linear recuurent models 보다 높은 성능을 보였으며 200만 토큰 이상의 긴 문맥으로 스케일이 가능함을 보여줌

# 1. Introduction

Transformer는 in-context learning과 ability to learn at scale 능력 덕분에 시퀀스 모델링의 SOTA 모델로 굳혀졌다. Transformer의 attention 메커니즘은 연관 기억(associative memory)의 역할을 한다. 이는 입력(query)이 주어졌을 때 유사한 과거 정보(query와 key 간의 유사도를 이용)를 찾아 가장 적합한 value를 찾는 과정이 associative memory가 입력과 가장 가까운 기억을 검색하는 방식과 유사하다는 것이다. 즉, Transformer는 현재 문맥(context)에 따라 다르게 작동하고 이것이 문맥에서 학습이 가능한 in-context learning을 의미한다.

그러나, Transformer 구조는 context length가 길어질수록 시간과 메모리 복잡도가 크게 증가하는 문제가 있다. 따라서 이와 같은 문제점은 현실 세계의 복잡한 문제를 해결할 때 문제가 된다. 

 

Transformer의 scalability 문제를 해결하기 위해 많은 연구들이 진행되었다. 그중 하나인 Linear Transformers는 attention의 softmax를 kernel function으로 대체하여 메모리 사용량을 줄였다. 이 구조는 Transformer를 linear recurrent network처럼 작동하게 만들었으며 결과적으로 Transformer만큼의 성능을 내지는 못했다. 이와 같은 결과는 linear 한 Transformer나 recurrent network가 scalability나 효율성 측면에서는 좋지만 아주 긴 문맥을 벡터나 행렬로 압축시키는 데는 한계가 있음을 보여주었다.

 

이 논문의 저자들은 효과적인 학습 패러다임에서는 인간의 두뇌와 유사하게 각기 독립적이면서도 상호 연결된 모듈들이 존재하며, 이러한 모듈 각각이 학습 과정에서 중요한 구성 요소를 담당한다고 주장한다. 

 

Memory perspective

 

• 메모리는 인간 학습의 핵심 요소이며, 기계 학습에서도 Hopfield Networks, LSTMs, Transformers와 같은 모델에 영감을 줌
• 기존 신경망 모델들은 메모리를 "입력에 의해 일어나는 뉴럴 업데이트"로 정의하고 학습을 "목표가 주어졌을 때 효과적인 메모리를 얻는 과정"으로 정의
• RNNs: 벡터 기반의 메모리 구조를 사용하며, (1) 입력을 기반으로 메모리를 업데이트하고, (2) 저장된 기억을 검색하여 활용
• Transformers: Key-Value 쌍을 활용한 "성장하는 메모리 구조"를 가지며, (1) 새로운 데이터를 메모리에 추가하고, (2) Query-Value 간 유사도를 기반으로 기억을 검색

 

• Transformer vs. Linear Transformer
  • Transformer는 모든 과거 데이터를 보존하지만,
  • Linear Transformer는 고정된 크기의 행렬 형태로 데이터를 압축하여 저장
• Linear RNN vs. Linear Transformer
  • Linear RNN은 벡터 기반 메모리를 사용
  • Linear Transformer는 행렬 기반 메모리를 사용

이러한 차이를 바탕으로, 저자는 다음과 같은 질문을 제기함:

1. 좋은 메모리 구조란 무엇인가?
2. 적절한 메모리 업데이트 방식은 무엇인가?
3. 효율적인 메모리 검색 과정은 무엇인가?
4. 여러 메모리 시스템을 통합하는 효율적인 아키텍처 설계 방법은?
5. 긴 문맥을 저장하는 데 깊은 메모리 모듈이 필요한가?

Contributions and Roadmap

이 논문에서는 위 5가지 질문에 답하기 위해 효율적이고 효과적으로 test time에 기억하는 것을 학습할 수 있는 long-term neural memory module을 설계하고 이를 신경망 아키텍처에 어떻게 통합할 수 있는지를 탐구했다.

 

1. Neural Memory

• Neural Memory는 인간의 장기 기억 시스템에서 영감을 받아 설계됨
• 메모리는 입력 데이터가 기대를 벗어날 때(surprising events) 더욱 강하게 기억됨
• Associative Memory Loss를 활용하여, 입력에 대한 신경망의 그라디언트를 기반으로 기억을 최적화함
• **Decay Mechanism (망각 메커니즘)**을 도입하여, 메모리 크기와 정보 중요도를 조절하여 더 효율적인 기억 관리를 수행
• 이 메커니즘은 경사 하강법(Gradient Descent), 모멘텀, 가중치 감소(Weight Decay)와 동등한 최적화 방식으로 작동

2. Titans Architectures

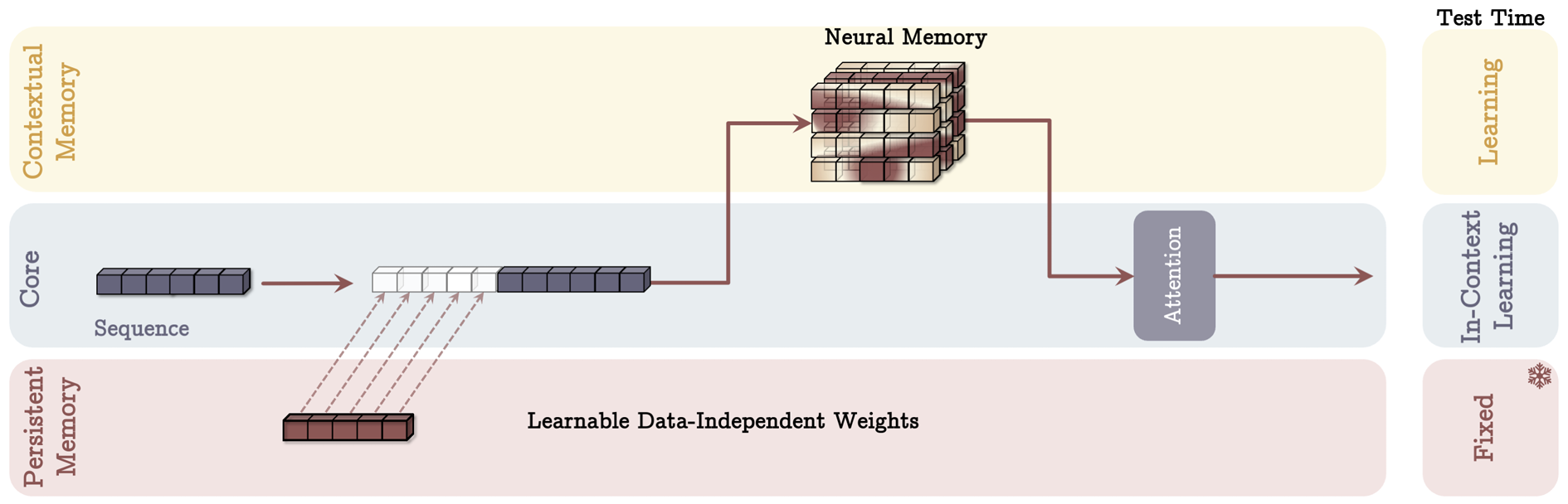
• Titans는 효율적인 장기 기억(Neural Memory)을 딥러닝 아키텍처에 통합한 신경망 아키텍처로, 세 가지 주요 모듈로 구성됨.
  1. Core: 단기 기억(Short-term Memory)을 담당하며, 제한된 윈도우 크기 내에서 Attention을 수행
  2. Long-term Memory: Neural Memory 모듈을 활용하여, 장기적인 기억을 저장 및 검색
  3. Persistent Memory: 특정 태스크(Task)에 대한 학습 가능하지만 data-independent 한 가중치 집합으로, 일반적인 지식(Knowledge)을 저장
• 메모리를 활용하는 세 가지 방식 제안:
  1. Context-based Memory
  2. Layer-based Memory
  3. Gated Memory Branch

3. Experimental Results

 

• Titans은 언어 모델링, 상식 추론, 시계열 예측, DNA 모델링 등 다양한 벤치마크에서 기존 순환 신경망(RNN)과 하이브리드 Transformer 모델을 능가함
• 동일한 컨텍스트 윈도우를 사용하는 Transformer보다도 더 높은 성능을 달성
• 2M 이상의 긴 컨텍스트 윈도우에서도 확장 가능하며, 기존 Transformer보다 효율적으로 동작

# 2. Preliminaries

Attention

 

 

$ W_q, W_k, W_v ∈ R^{d_{in} × d_{in}} $ 위에서 언급했듯이 성능은 좋지만 메모리 소비량이 많고 throughput(단위 시간당 처리할 수 있는 데이터의 양)이 낮음.

 

Efficient Attentions

대표적인 기법으로 kernel-based(linear) attention이 있다. 기존 Attention의 softmax를 kernel function $ \phi(.,.) $ 로 대체하고 이는 다음을 만족한다. $ \phi(x, y) = \phi(x)\phi(y) $

 

 

$ \sum_{j=1}^{i} \phi(K_j) $ 와 $ \sum_{\ell=1}^ \phi(K_{\ell}) $은 매 스텝마다 재사용되어 throughput이 올라가게 된다. 만약 kernel을 identity matrix로 정의할 경우 위 식은 아래와 같이 recurrent 하게 나타낼 수 있다.

 

Modern Linear Models and Their Memory Perspective

Linear RNN에서의 Memory 개념

• RNN에서는 숨은 상태(hidden state)를 벡터 기반의 메모리로 간주하며, 반복적으로 업데이트됨.
• 일반적인 Recurrent Neural Network (RNN) 모델은 다음과 같이 정의됨:
  • 쓰기 연산 (Write Operation): $ \mathcal{M}_t = f(\mathcal{M}_{t-1}, x_t) $
  • 읽기 연산 (Read Operation): $ y_t = g( \mathcal{M} _t, x_t) $
• Linear Transformers도 RNN과 유사하게 Key-Value Memory를 행렬(Matrix) 단위로 저장하며, 이로 인해 메모리 관리가 중요한 문제가 됨

 

Linear Transformer에서의 Memory Overflow 문제

• Linear Transformer는 데이터를 Key-Value 형태로 지속적으로 추가하며, 이는 Memory Overflow 문제를 발생시킴
• 이를 해결하기 위해 두 가지 접근법이 연구됨:
  1. Forget Mechanism (망각 메커니즘)
     • 일부 모델은 불필요한 기억을 자동으로 삭제하는 Forget Gate를 추가하여 메모리를 최적화
     • 예: GLA, LRU, Griffin, xLSTM, Mamba2 등
  2. Improving Write Operations (쓰기 연산 개선)
     • **Delta Rule (Widrow and Hoff, 1988)**을 적용하여, 새 데이터를 추가하기 전 기존 데이터를 먼저 제거하는 방식

Memory Modules

• Memory는 뉴럴 네트워크에서 중요한 구성 요소이며, 다양한 방식으로 활용됨
• Hebbian Learning (Hebb, 2005)과 Delta Learning (Prados & Kak, 1989)과 같은 고전적인 학습 법칙이 메모리 업데이트에 적용됨
• 최근 연구들은 기존 메모리 시스템이 momentary surprise에 기반을 두어 sequence에서의 token flow를 반영하지 못하고 Forget Gate가 없어 장기 기억 유지에 취약하다는 점을 지적하고, 이를 해결하기 위한 새로운 구조를 탐색하고 있음

# 3. Learning to Memorize at Test Time

3장에서는 장기 기억(long-term memory)의 부족 문제를 해결하고, 모델이 학습, 망각(forget), 정보 검색(retrieve)을 할 수 있도록 하는 신경망 기반 장기 기억 모듈(Neural Long-Term Memory Module)을 제안함.

 

• Section 3.1: Neural Memory의 동기 및 설계(design) 논의
• Section 3.2: 빠르고 병렬화 가능한 학습을 통해 모델을 최적화하는 방법 설명
• Section 3.3: Persistent Memory Module을 추가하여, 데이터에 독립적인 학습 가능한 매개변수(learnable but data-independent parameters)를 활용하여 태스크의 메타 정보를 학습

3.1 Long-term Memory

1. Long-term memory의 필요성

• 기존 Language Model (LLM)들은 훈련 데이터를 단순히 암기하지만, 이는 일반화 성능을 저하시킬 위험이 있음.
• 따라서, 훈련 데이터의 정보를 단순 저장하는 것이 아니라, 테스트 시점에서도 새로운 정보를 학습하거나 망각할 수 있도록 하는 메타 모델(meta-model)이 필요.

2. Learning Process and Surprise Metric

사람이 예상치 못한 사건을 더 잘 기억하는 것처럼, 모델도 입력 데이터의 "예상 밖의 정도 (Surprise)"를 기반으로 학습할 수 있음. 이를 위해 Surprise Score를 정의하고, 이 값을 기반으로 메모리를 업데이트함 

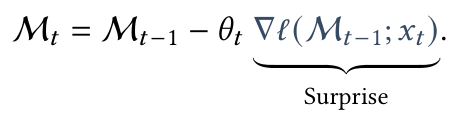
• $ \theta_t $ : 학습률(learning rate) 역할
• $ \nabla \ell( \mathcal{M} _{t-1};x_t) $ : Surprise Score를 기반으로 한 메모리 업데이트

그러나 이 방식은 특정 이벤트가 너무 큰 Surprise를 가지면 이후 이벤트들이 무시될 가능성이 있음.

• 이를 해결하기 위해 Surprise를 두 단계로 분리:
  • 1. Past Surprise: 과거 서프라이즈 누적값 
    2. Momentary Surprise: 새로운 입력에서 발생하는 서프라이즈 

위 식은 momentum을 포함한 gradient descent 식과 유사함. 즉, $ S_t $가 momentum 역할을 하며 시간(sequence length)에 따른 surprise의 기억으로 작동함. 

• $ \eta_t $ : Data-dependent surprise decay. Past surprise가 얼마나 감소할지를 결정
• $ \theta_t $ : Momentary surprise가 최종 surprise에 얼마나 반영되어야 하는지를 결정. 이 역시 Data-dependent 한 변수.

두 변수 모두 data-dependent 하다는 의미는 모두 입력으로 $ x_t $를 받아 출력 값을 내뱉는 neural network라는 의미이다. 두 변수가 data-dependent 한 성질을 가지는 것은 이 구조에서 매우 중요하다. 

• $ \eta → 0 $ : 문맥 자체가 바뀌는 경우 직전 surprise를 무시하는 것이 좋다
• $ \eta → 1 $ : 입력 토큰들이 같은 문맥 내에 존재하는 경우 직전 surprise를 반영하는 것이 좋다.

3. Associative Memory & Forgetting Mechanism

• Associative Memory를 활용하여 Key-Value Pair로 데이터를 저장:
  • 입력 $ x_t $ ​를 Key($ k_t $)와 Value($ v_t $)로 변환: $ k_t = x_tW_K $, $ v_t = x_tW_V $​
  • 이때 메모리 모듈은 Key와 Value 간의 관계를 학습하여, 특정 Key가 주어졌을 때 적절한 Value를 검색 가능.

위의 loss function을 최적화하는 과정은 neural memory module(meta model)의 inner-loop에서 진행된다. 즉, test time에 학습을 하게 되는 것이다. Inner-loop에서는 $W_K$와 $W_V$가 하이퍼 파라미터처럼 작용해 module $ M $의 weight만 업데이트하고 전체 아키텍처의 다른 파라미터들은 outer-loop에서 업데이트한다.

• 망각(Forging) 메커니즘 추가
  • 너무 많은 데이터가 저장되면, 불필요한 정보도 함께 저장될 가능성이 높음.
  • 이를 해결하기 위해, 가중치 $ \alpha_t $​를 추가하여 메모리의 일부를 점진적으로 삭제 가능​
  • $ \alpha_t → 1 $이면 메모리를 지우는 효과, $ \alpha_t → 0 $이면 과거 데이터를 유지

 

4. Memory Architecture & Retrieval

• 메모리 모델은 간단한 MLP (Multi-Layer Perceptron) 구조를 사용하지만, 더 깊은 신경망(Deep Memory)이 필요할 수도 있음. (논문의 저자들은 long-term memory를 neural network 형태로 디자인하는 것의 동기부여와 architecture에 통합시키는 것을 더 중요시 여김)
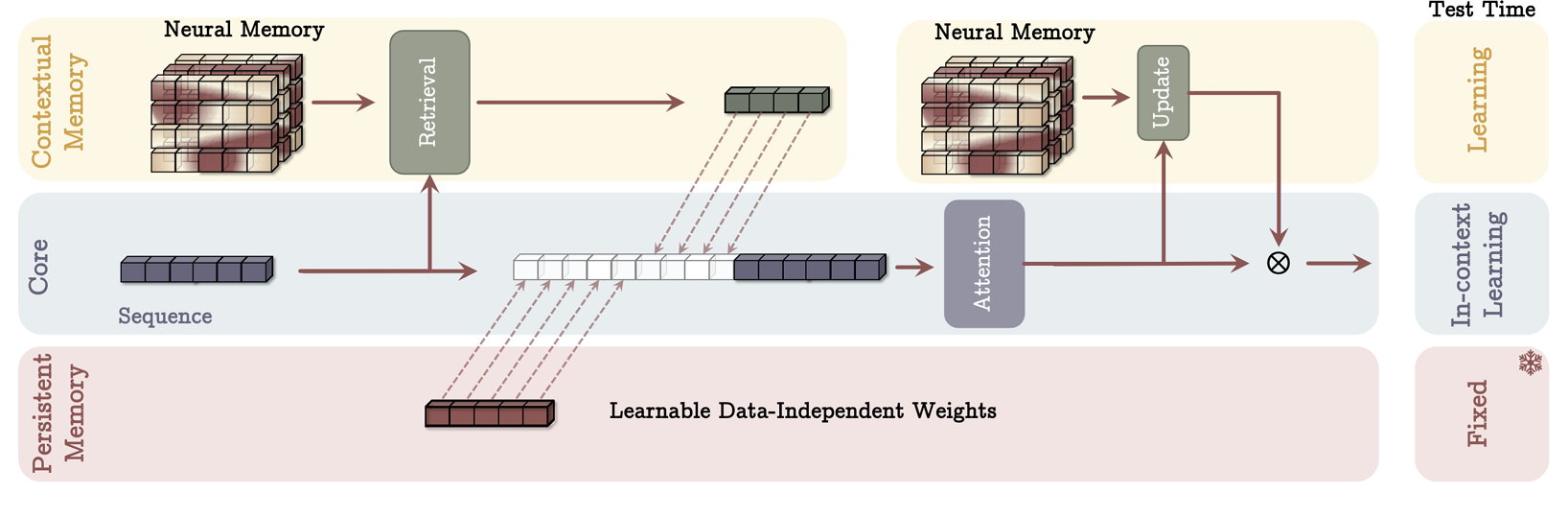
• 메모리 검색 방법:
  • Input $ x_t $에 대하여 Linear Layer ($ W_Q $)를 적용해 얻은 query $ q_t $를 이용하여 Memory에서 관련된 정보를 검색
  • 아래와 같이 Neural memory module에 query를 입력 값으로 넣어 memory를 반영.​

*는 weight update이 일어나지 않음을 의미

 

 

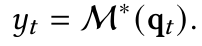
3.2 How to Parallelize the Long-term Memory Training

1. Long-term Memory 학습의 계산량 문제

• 메모리 모듈 학습은 Gradient Descent with Momentum & Weight Decay 방식을 따름.
• 그러나 $ O(N) $ FLOPs가 필요, 즉 시퀀스 길이 NNN이 길어질수록 연산량이 선형적으로 증가.
• 이를 해결하기 위해 Mini-Batch Gradient Descent 및 MatMul 연산을 활용한 병렬화 기법을 적용.

2. Mini-Batch Gradient Descent를 통한 병렬화

Sequence를 크기 b >= 1의 chunck로 나누어 기존 식을 변형, Mini-Batch Gradient Descent 방식으로 표현:

여기서:

• $ t^{'} = t - mod(t, b) $, mod(t, b)는 t를 b로 나눈 나머지
• $ \beta_i = \prod_{j=1}^{i} (1 - \alpha_j) $
  → Forget Factor를 누적한 값.
• Mini-Batch를 사용하여 여러 개의 $ x_i $에 대해 병렬 연산 가능.

3. Matmul 연산을 활용한 병렬화

Gradient 계산을 다음과 같이 변형하여, Matrix-Vector 연산(MatMul)으로 변환:

여기서:

• $ \Theta_b = diag([\theta_1, \theta_2,..., \theta_b]) $
  → 각 Mini-Batch의 학습률을 행렬로 표현
• $ B_b $​
  → Forget Factor를 포함하는 행렬

즉, 각 Mini-Batch의 Gradient를 한 번에 계산할 수 있도록 변형하여 계산량을 줄임.

 

4. Momentum term을 적용한 병렬화

Surprise Score $ S_t $를 업데이트할 때, Momentum Term을 적용:

​

여기서 $ u_t = \nabla \ell( \mathcal{M} _t; x_t) $

→ 즉, Surprise Score를 한꺼번에 계산하여 병렬화 가능.

 

5. Chunk-wise Parameterization을 통한 연산 최적화

• $ \alpha_t, \theta_t, \eta_t $​는 원래 입력 $ x_t $​에 따라 다르게 학습됨.
• 하지만 Chunk 단위로 동일한 값을 사용하면 연산 속도를 더 빠르게 할 수 있음.
• 즉, 각 Chunk 내에서 동일한 Forget Factor, Learning Rate 사용 가능.

이렇게 하면 Time-Invariant System (LTI) 형태로 변형 가능하여, 병렬 연산이 더욱 쉬워짐.

논문에서는 parameter들을 token들의 function으로 지정. 

 

3.3 Persistent Memory

1. Persistent Memory의 정의 및 구조

• 기존의 Long-term Memory는 입력에 따라 변하는 Input-dependent Memory.
• 그러나 Persistent Memory는 입력과 무관한(Task-specific) 정보를 저장하는 Learnable Parameters.
• 이를 위해, 학습 가능한 파라미터 $ P = [p_1 p_2 \dots p_{N_p}] $를 입력 시퀀스 앞에 추가:

• 즉, Persistent Memory는 학습 가능한 "고정된" 토큰 역할을 하며, 입력 시퀀스 앞부분에 추가됨.

2. Persistent Memory의 3가지 관점

2-1. Memory Perspective

• 일반적인 Long-term Memory는 입력에 따라 변하는 Contextual Memory.
• 하지만 Task-specific 정보(태스크를 수행하는 방법 등)는 입력에 따라 변하면 안 됨.
• 따라서, 입력과 독립적인 Learnable Parameters를 추가하여, Task Knowledge를 저장.

2-2. Feedforward Network Perspective

• Transformer에서 Attention 이후의 Feedforward Network (FFN)도 일종의 Memory 역할을 수행.
• 논문에서는 FFN이 Attention의 K, V 행렬과 유사한 역할을 한다고 설명.
• Persistent Memory는 Attention에서 K, V 행렬이 하는 역할과 비슷하게 작동하며, Attention Weights를 입력과 무관하게 조정하는 역할.

• 여기서 $ W_k, W_v $​가 Attention의 Key, Value 행렬처럼 동작.
• 즉, Persistent Memory는 Attention Weights가 특정 정보를 유지할 수 있도록 도움.

3. Technical Perspective

• Transformer의 Causal Mask(미래 정보를 참조하지 못하도록 막는 기법)는 종종 초기 토큰에 Bias를 줌.
• 즉, Attention Weights가 시퀀스의 앞부분(초기 토큰)에 편향되는 문제 발생.
• Persistent Memory를 입력 시퀀스 앞에 추가하면, Attention Weights를 더 균형 있게 분배할 수 있음.

# 4. How to Incorporate Memory

뉴럴 메모리를 아키텍처에 효과적으로 통합하는 방법을 제안함.

• 기존 Transformer의 K-V 매트릭스는 단기 메모리로 해석되며, 현재 컨텍스트 (context window size 범위 내) 만을 고려함.
• 뉴럴 메모리는 지속적으로 데이터를 학습하고 저장할 수 있어 장기 메모리 역할을 수행할 수 있음.
• Titans 모델의 3가지 변형을 제시

4.1 Memory as Context

Memory as a Context(MAC) Architecture

 

• 입력 시퀀스($ x ∈ \mathbb{R}^{N×d_{in}} $)를 고정된 크기의 세그먼트 $ S^{(i)}, i = 1,\dots N/C $로 나눔.
• 현재 세그먼트 $ S^{(t)} $가 들어오면 현재 컨텍스트(current context)로, 이전 세그먼트들을 historical 정보로 고려한다.
• 즉, $ \mathcal{M}_{t-1} $을 세그먼트 $ S^{(t)} $ 이전의 장기 기억 상태로 정의하고 아래의 식을 통해 $ S^{(t)} $에 해당하는 과거 정보를 아래의 식을 통해 구한다.

 

• 이때 $ q_t = S^{(t)}W_Q $로 input context $ S^{(t)} $를 query로 사용했다.

• historical information $ h_t $와 persistent memory를 모두 사용하여 attention 모듈의 input으로 활용한다.

• $ y_t $를 이용하여 $ \mathcal{M}_{t-1} $의 weight을 forward pass로 업데이트하고 최종 출력 계산

MAC 아키텍처의 주요 장점

 

• Attention을 이용해 과거 컨텍스트와 현재 컨텍스트를 모두 고려 가능
  • 불필요한 정보를 저장하는 것이 아니라, 중요한 정보만 선별하여 장기 메모리에 저장.
• 메모리 효율성 향상
  • 모든 토큰을 저장하는 것이 아니라, Attention을 활용하여 유용한 정보만 저장하여 메모리 용량을 절약함.
• 테스트 시에도 지속적인 학습 가능
  • (i) Persistent Memory는 학습되지 않고 고정됨 (Task-specific Knowledge 보존)
  • (ii) Attention 모듈은 In-Context Learner 역할을 수행함
  • (iii) 뉴럴 메모리는 테스트 시에도 지속적으로 업데이트됨 (Long-term Memory 유지)

4.2 Gated Memory

Memory as a Gate(MAG) Architecture

이 변형에서는 두 가지 방식으로 뉴럴 메모리를 업데이트함.

1. 입력 데이터를 직접 사용하여 장기 메모리를 업데이트하는 방식
2. Sliding Window Attention (SWA) 기법을 사용하는 방식

1) Sliding Window Attention 기반 메모리 업데이트

$ \mathcal{M}(x) $는 모든 토큰을 반복적으로 업데이트 한 최종 출력값 의미

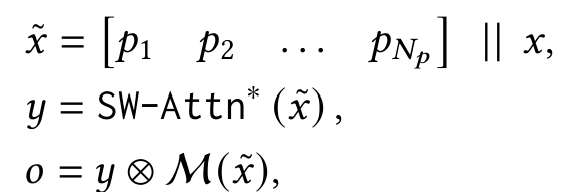
• Persistent Memory $P$ 를 입력 $x$ 와 결합하여 새로운 입력 $ \tilde{x} $ 생성 
• Sliding Window Attention (SWA) 적용하여 출력을 계산 
• 출력 $y$ 를 뉴럴 메모리 $ \mathcal{M}(\tilde{x}) $ 와 결합하여 최종 결과 생성
  • 여기서 $ \otimes $ 는 비선형 게이팅 함수 (non-linear gating)로 활용됨.
  • 실험에서는 $y$ 와 $ \mathcal{M}(\tilde{x}) $ 를 정규화 후(learnable vector-value 사용) 비선형 활성화 함수 $ \sigma(.) $ 를 적용.

• MAC: 입력을 세그먼트로 나누고, 각 세그먼트 내에서만 어텐션을 적용. Long-term memory와 persistent memory를 추가하여 장기 정보 유지.
• MAG: Sliding Window Attention(SWA)을 사용하여 연속적으로 어텐션을 적용하며, 뉴럴 메모리를 활용해 long-term memory를 추가.
• MAC은 세그먼트 기반으로 메모리를 저장하고, MAG는 윈도우 기반으로 메모리를 업데이트하여 더 유연한 메모리 활용 가능. 

4.3 Memory as a Layer

 

Memory as a Layer(MAL) Architecture

 

• Memory as a Layer (MAL): 신경 기억 모듈을 심층 신경망의 하나의 레이어로 사용하는 방식이다. 
• 구조: 입력 $x$ 에 대해 먼저 persistent memory $P$ 를 추가한 후, neural memory module을 적용한 결과를 얻고, 이후 슬라이딩 윈도우 어텐션을 수행하여 최종 출력을 만든다.

• 문제점: 모델의 성능이 각 레이어의 한계에 의해 제한되며(∵sequence model), 어텐션과 신경 기억 모듈이 상호 보완적으로 데이터를 처리하는 장점을 충분히 활용하지 못할 수 있다.
• Memory Without Attention: 논문의 저자들은 주어진 MAL 구조에서 어텐션을 제거한 LMM을 실험적으로 평가하며, 장기 기억 모듈이 독립적으로 강력한 모델로 작동할 수 있는지 분석한다.

4.4 Architectural Details

 

• Residual Connections & Normalization: Titans 모델 구현에서는 모든 block에서 residual connection을 사용하며, 비선형 활성화 함수로 SiLU를 적용하고, query, key, value를 계산할 때 ℓ₂-norm으로 정규화한다.
• Convolution: 최신 선형 재귀 모델을 따라 1D depthwise-separable convolution을 query, key, value 투영 후에 적용하여 성능 향상과 연산 효율성을 높인다.
• Gating: 최신 아키텍처를 따라 선형 레이어 기반 정규화 및 게이팅을 최종 출력 투영 전에 적용한다.

 

# 5. Experiments

 

논문의 5장 "Experiments"에서는 Titans 모델과 그 변형을 다양한 벤치마크에서 평가하며, 다음과 같은 주요 연구 질문을 다룬다.

1. Titans 모델이 다양한 다운스트림 태스크에서 기존 모델 대비 얼마나 우수한 성능을 보이는가?
2. Titans 모델의 실제 컨텍스트 길이는 얼마인가?
3. Titans 모델이 컨텍스트 길이에 따라 어떻게 확장(scale)되는가?
4. 기억 모듈의 깊이가 성능과 효율성에 미치는 영향은?
5. Titans의 각 구성 요소가 성능에 기여하는 바는 무엇인가?

5.1 Experimental Setup

• 모델 구성:
  • Titans 모델의 세 가지 변형:
    1. Memory as a Context (MAC)
    2. Memory as Gating (MAG)
    3. Memory as a Layer (MAL)
  • 또한, 뉴럴 메모리 모듈 단독 모델도 비교 대상으로 포함.
• 모델 크기:
  • 170M, 340M, 400M, 760M 파라미터 크기의 모델을 사용.
• 학습 데이터:
  • FineWeb-Edu 데이터셋에서 15B~30B 토큰을 샘플링하여 학습​.
• 비교 대상:
  • Transformer++, RetNet, Gated Linear Attention (GLA), Mamba, DeltaNet, TTT 등 최신 Transformer 및 선형 순환 신경망 모델​.

5.2 Language Modeling

• Titans 모델은 기존의 Transformer 및 순환 모델보다 Perplexity, accuracy 측면에서 우수한 성능을 보임.
• Titans의 뉴럴 메모리 모듈과 TTT와 같은 Gradient 기반 순환 모델의 비교는 weight decay의 중요성을 보여줌.
• MAL보다 MAG, MAC의 성능이 더 높게 나옴. 

 

5.3 Needle in a Haystack

• 모델이 긴 문서에서 특정 정보를 검색하는 능력을 평가하는 벤치마크.
• 모델의 실질적 효과적인 문맥 길이를 측정하는 것이 목표.
• S-NIAH task를 2K, 4K, 8K, 16K 길이의 문맥으로 실험을 진행

• 3가지의 task에서 모두 Titans가 최고 성능을 보임
  • TTT와 비교하여, neural memory가 momentum과 forgetting mechansim으로 인해 메모리 용량 관리가 더 용이.
  • Mamba2 (forgetting mechansim 존재)와 비교하여, Titans의 non-linear deep memory가 메모리 관리에 더 용이함을 보여줌. 또한 Mamba2는 기억을 제거하는 기능이 없어 길이가 늘어남에 따라 심각한 성능 저하를 보여줌.
  • DeltaNet (기억을 제거할 수는 있지만 지우는 것은 불가능)과 비교하여, forgetting mechansim의 중요성을 보여줌.
• Titans variants 중에서는 MAC가 최고 성능을 보임.

5.4 BABILong Benchmark

NIAH 태스크보다 난이도가 높은 태스크로, 매우 긴 컨택스트에서 논리적 추론을 수행해야 한다.

• Few-shot 설정에서는 large pre-trained 된 모델과 비교하여 Titans(MAC) 모델이 Mamba2.8 B, RWKV-6-7B, RecurrentGemma-9B, Gemma-9B, Llama3.1-8B, GPT-4, GPT-4o-mini 등의 다양한 최신 모델을 능가하는 성능을 보였다. 특히 Titans은 훨씬 적은 수의 파라미터를 사용하면서도 높은 성능을 유지했다.
• Fine-tuning 설정에서는 Titans(MAC)을 작은 크기의 모델(Mamba, RMT), Retrieval-Augmented Generation(RAG)을 적용한 대형 모델(Llama3.1-8B), 그리고 초대형 모델(GPT-4, GPT-4o-mini, Qwen2.5-72B, Llama3.1-70B)과 비교했다. Titans은 모든 모델, 심지어 GPT-4와 같은 대형 모델보다도 뛰어난 성능을 보였다.
• 메모리 활용 방식 차이: 기존 Transformer 기반 메모리 모델인 RMT는 히스토리 데이터를 16 크기의 벡터로 압축하는 반면, Titans은 과거 정보를 모델의 파라미터로 직접 인코딩하여 더 뛰어난 성능을 발휘했다.
• 효율성 측면: RAG를 적용한 Llama3.1-8B 모델이 Titans보다 70배 더 많은 파라미터를 사용했음에도 불구하고 성능이 낮았으며, Titans의 효율적인 메모리 설계가 뛰어난 성능을 내는 중요한 요인임을 보여줬다.

 

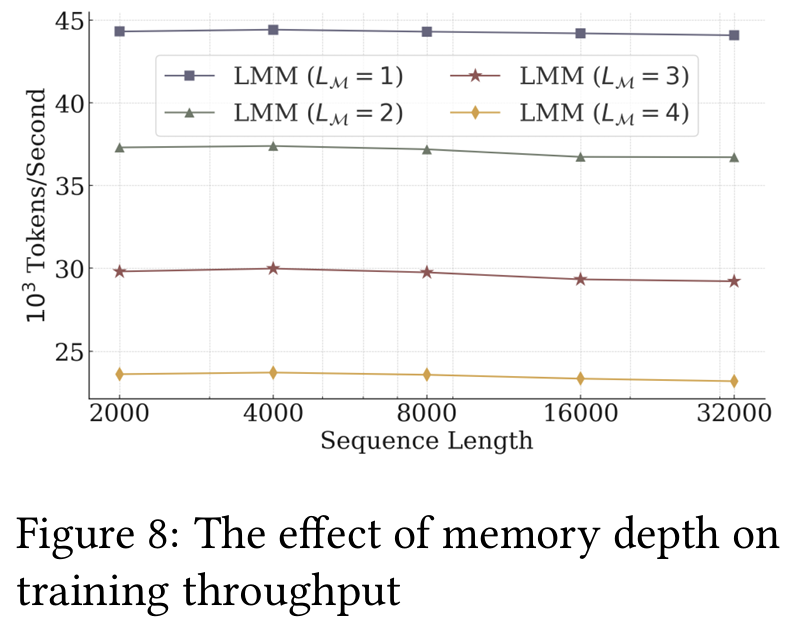
5.5 깊은 메모리의 효과

• 메모리 깊이(𝐿𝑀=1,2,3,4)가 성능에 미치는 영향을 평가.
• 깊은 메모리가 더 긴 문맥에서 강력한 성능을 제공하지만, 계산 비용 증가의 트레이드오프가 존재​.

 

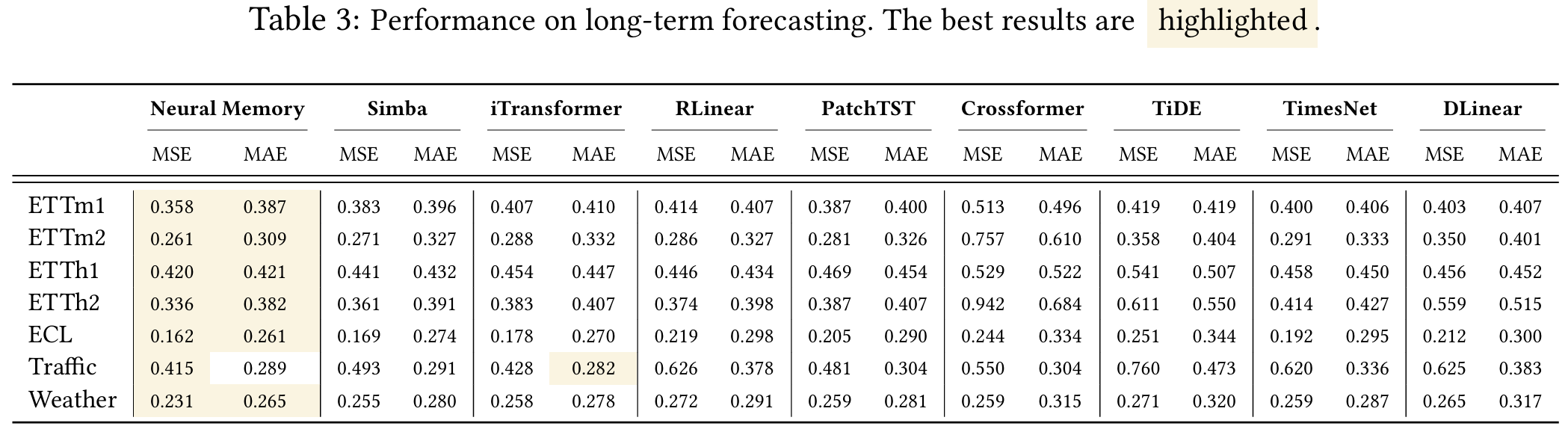
5.6 Time Series Forecasting

• Titans 모델이 시계열 데이터를 활용한 예측에서 기존 Transformer 및 Mamba 기반 모델보다 향상된 성능을 보임​.
• Simba framework를 활용하였으며, 기존의 Mamba module을 neural memory로 교체하여 실험을 진행.

 

5.7 DNA Modeling

• GenomicsBenchmarks 데이터셋에서 Titans 모델의 DNA 서열 분석 성능을 평가.
• 기존 SOTA 모델과 경쟁할만한 성능을 보여줌.

 

5.8 Efficiency

• Titans의 효율성을 평가한 결과, Mamba2 및 Gated DeltaNet보다 약간 느리지만, 이는 더 깊은 메모리 구조와 더욱 표현력 있는 전이 과정(memory update) 때문으로 분석됨.
• 반면, Titans(MAL)는 기존 모델보다 빠른 처리 속도를 보였으며, 이는 Flash-Attention을 활용한 최적화된 커널 덕분.

5.9 Ablation Study

• Titans의 다양한 구성 요소를 제거하며 기여도를 분석.
• Weight decay, momentum, convolution, persistent memory 모두 각가 성능에 기여함을 확인.
• MAC, MAG는 MAL보다 높은 성능을 보임. 이는 train 시간과 표현 성능의 trade-off로 figure 9의 결과와 이어짐.