https://arxiv.org/abs/1609.02907
GCN (Graph Convolutional Networks)는 그래프의 형태로 저장된 데이터의 node와 node 사이를 잇는 edge를 분석하는 GNN (Graph Neural Network)의 간단한 일종이다.
CNN이 convolutional filter의 global weight parameter를 이용해 연산비용을 줄인 것처럼, GCN도 global parameter이 적은 graph convolution을 각 node와 k-단계로 인접한 node들에 적용해 aggregation을 수행한다고 이해할 수 있다.
해당 논문은 Thomas N. Kipf이 암스테르담 대학교의 Max Welling 교수 (VAE의 개발자) 밑에서 박사과정 도중 작성한 논문으로 Kipf 박사는 졸업 이후 구글 딥마인드에서 Staff Research Scientist로 근무하고 있다.
0. Abstract
저자들은 그래프에 직접 적용이 가능한 효율적인 유사-CNN 모델 (GCN)을 이용해, 그래프 데이터에서 반지도학습 (semi-supervised learning)을 수행한다.
특히 spectral graph convolution (그래프에 푸리에 변환을 수행한 후 convolution 적용)의 local한 1차 근사를 통해 효율을 높여, 학습 복잡도가 edge 수에 선형비례하고 node의 feature 뿐만 아니라 그래프의 local 구조까지 담는 은닉층을 구성한다.
저자들이 제안한 모델은 실험에서 관련 모델보다 월등히 좋은 성능을 기록한다.
1. Introduction
그래프에서 각 node의 label이 조금만 존재할 때, 모든 node를 분류하는 그래프 기반 반지도학습 문제는 손실 함수를 다음과 같이 라플라스 정규화 항을 추가해서 모든 node에 적용해서 풀 수 있다.
$$\mathcal{L}=\mathcal{L}_ {0} + \lambda\mathcal{L}_ {reg}, \mathcal{L}_ {reg} = \sum_ {i.j}A_{ij}||f(X_i)-f(X_j)||^2=f(X)^{T}\Delta f(X)\tag{1}$$
그러나 해당 방법은 인접한 node는 label이 유사할 것이라는 가정 하에서 출발한만큼, 그래프에서 edge가 node의 유사성이 아니라 다른 정보를 담을 경우 그래프를 온전히 표현하지 못한다.
따라서 이 논문에서는 그래프의 구조를 인공신경망 모델 $f(X,A)$로 직접 학습하고 label이 있는 node에서 지도학습을 통해 $\mathcal{L}_ {0}$를 최적화해, 그래프에 대한 가정이 필요한 정규화식을 배제하는 대신 그래프의 인접행렬 $A$를 학습함으로써 label이 있는 node에서 얻은 gradient 정보를 전체 그래프로 퍼뜨릴 수 있게 했다.
해당 논문은 크게
- 그래프의 푸리에 변환의 1차 근사를 이용한 인공신경망 레이어 구축 방법을 제시하고,
- 1의 방법으로 구성된 GNN 모델이 빠르고 확장가능한 node 분류가 가능함을 입증한다.
2. Fast Approximate Convolutions on Graphs
해당 논문은 Hammond et al., 2011 [1]에서 제시된 그래프의 푸리에 변환 기반 convolution식 (2)에서 연산비용을 줄이기 위해 Chebyshev 다항식 $T_ k(x)$로 근사한 (3)에서 시작해, 1차로 근사하여 시작 node 반경으로 인접 node만 고려하고 편의성을 위해 최대 eigenvalue $\lambda_ {max}$의 값을 2로 설정했다.
$$g_ {\theta}\star x=U g_ {\theta}U^{T}x\tag{2}$$
$$g_ {\theta'}\star x=\sum_{k=0}^{K}\theta'_ {k}T_{k}(\tilde L)x\tag{3}$$
이를 통해 convolution filter $g_ {\theta'}$의 식을 (4)처럼 도출해, 두 개의 학습 parameter $\theta_0, \theta_1$만을 남겼다.
$$g_ {\theta'}\star x\approx \theta'_ {0}x+\theta'_ {1}(L-I_ {N})x=\theta'_ {0}x-\theta'_ {1}D^{-\frac{1}{2}}AD^{-\frac{1}{2}}x\tag{4}$$
해당 선형식은 하나의 convolution layer에 사용되고, 여러 layer을 겹쳐서 다양한 정보를 학습하는 모델을 구성할 수 있다.
저자들은 실제로 모델을 구성할 때 과적합을 방지하고 연산비용을 줄이기 위해 (6)처럼 $\theta=\theta'_ {0}=-\theta'_ {1}$인 단일 parameter로 설계했고, vanishing/exploding gradient을 최소화하기 위해 (7)과 같은 재정규화 기법 (renormalization trick)을 사용했다.
$$g_ {\theta}\star x\approx \theta \left ( I_ {N}+D^{-\frac{1}{2}}AD^{-\frac{1}{2}} \right )x\tag{6}$$
$$I_ {N}+D^{-\frac{1}{2}}AD^{-\frac{1}{2}} \to \tilde D^{-\frac{1}{2}}\tilde A\tilde D^{-\frac{1}{2}}, \tilde A=A+I_ {N}, \tilde D_ {ii}=\sum_ {j} \tilde A_ {ij}\tag{7}$$
이렇게 구성된 모델은 C개의 입력채널의 그래프 (각 node가 C-차원 feature을 가짐)에 대해 F개의 convolutional filter을 적용할 경우 시간복잡도가 $O(|\mathcal{E}|FC)$로 edge의 개수 $|\mathcal{E}|$에 선형 비례했다고 저자들은 밝혔다.
3. Semi-Supervised Node Classification
간단하게 구현된 모델 $f(X,A)$를 이용해 반지도학습을 통한 node 분류를 수행할 경우, 그래프의 연결 구조에 정보가 담긴 참조문헌 그래프 등의 그래프에도 폭넓게 적용이 됨을 알 수 있다.
일부 node만 label이 존재하고 인접행렬 A가 대칭행렬인 그래프에 2-layer GCN을 적용하는 예시에 대해 $\hat{A}=\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}$를 먼저 계산한다면 forward propagation은 (8)처럼 나오고, label가 존재하는 node에 대해 (9)의 cross-entropy 손실함수를 최소화해 학습했다.
$$Z=f(X,A)=\text{softmax} \left ( \hat{A} \text{ReLU} \left ( \hat{A}XW^{(0)} \right ) W^{(1)} \right )\tag{8}$$
$$\mathcal{L}=-\sum_ {l \in \mathcal{Y}_ {L}}\sum_ {f=1}^{F}Y_ {lf} \text{ln}Z_ {lf}\tag{9}$$
이 논문에서는 minibatch stochastic gradient descent로 weight $W^{(0)}, W^{(1)}$을 학습했다.
4. Related Work
이 논문에서는 그래프 기반 반지도학습을 크게 그래프 라플라스 정규화 기법 [2-4]과 그래프 임베딩 기법 [5-9]으로 나눠서 소개했다.
특히 그래프 임베딩은 skip-gram 모델을 바탕으로 random walk 등을 사용해서 임베딩을 생성한다고 했다.
그래프에 적용하는 인공신경망은 RNN을 시초로 하여 노드의 연결성에 따른 weight를 부여해 확장이 어려운 CNN 기반 GNN 등을 소개했다. 저자는 기존 연구와 달리 이 논문은 여러 개의 간소화 기법을 도입해 대형 그래프에서 반지도학습을 수행한다고 주장했다.
5. Experiments
저자는 제안한 GCN 모델을 참조문헌 네트워크에서 문헌 분류, 지식 그래프에서 추출된 이분그래프에서 개체 분류에서 검증하고 다양한 그래프 확산 방법 및 임의의 그래프에서 소요 시간 등을 실험했다.
데이터셋은 Yang et al. (2016) [9]에서처럼 Citeseer, Cora, Pubmed 참조문헌 네트워크와 NELL 지식 그래프를 사용했다.
참조문헌 네트워크 데이터셋 학습 과정에서 Cora에서만 hyperparameter 튜닝을 한 후 동일 parameter로 Citeseer, Pubmed 데이터셋에서 검증을 했다.
Baseline 모델들은 위 4장에서 언급된 [2,3,4,6,9] 모델을 사용했다. 또한 Lu & Getoor (2003) [10]에서 소개된 점층분류알고리즘 (ICA)와도 비교했다.
6. Results
각 데이터셋별 분류 정확도는 다음 그림과 같았다.

Forward 확산 기법에 따른 분류 정확도는 다음과 같았다.

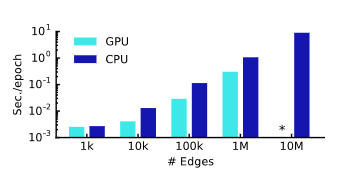
생성된 랜덤 그래프에서 학습 소요 시간은 다음과 같았다.
7. Discussion
기존 모델에 비해 이 논문이 제시한 GCN 모델은 월등히 좋은 성능을 기록했다.
그 원인으로 기존 그래프 기반 라플라스 정규화 모델들은 노드 간 유사성만 고려하기 때문에 정확도의 한계가 있었고, skip-gram 기반 임베딩 기법은 최적화하기 어려운 학습기법이었다고 저자는 추론했다.
해당 GCN 모델은 기존 모델들의 취약점을 보완하면서 시간복잡도 또한 우월했다. 기존 ICA 기법에 비해서도 좋은 성능을 기록했다.
논문의 한계로 데이터셋의 크기와 선형적으로 비례하는 메모리 할당량과 무방향 그래프에 한정된 적용, CNN 기법을 적용하기 위해 가정한 locality와 자기 자신으로의 edge와 인접 node로의 edge 간 대등함 등을 꼽았다. 전자의 경우 반도체의 발달로 어느 정도 해결이 가능하나 후자는 데이터셋에 따라 어느 정도의 보완이 필요할 것으로 보인다.
참조 문헌
[1] D.K. Hammond, P. Vandergheynst, R. Gribonval, "Wavelets on graphs via spectral graph theory," Appl. Comput. Harmon. Anal. 30 (2011), pp.129--150.
[2] X. Zhu, Z. Ghahramani, J. Lafferty, "Semi-supervised learning using gaussian fields and harmonic functions," Int. Conf. Mach. Learn. (ICML) 3 (2003), pp.912--919.
[3] M. Belkin, P. Niyogi, V. Sindhwani, "Manifold regularization: A geometric frame-work for learning from labeled and unlabeled examples," Journ. Mach. Learn. Res. (JMLR) 7 (2006), pp.2399--2434.
[4] J. Weston, F. Ratle, H. Mobahi, R. Collobert, "Deep learning via semi-supervised embedding," Neural Networks: Tricks of the Trade, Springer (2012), pp. 639–-655.
[5] T. Mikolov, I. Sutskever, K. Chen, G.S. Corrado, and J. Dean, "Distributed representations of words and phrases and their compositionality," Adv. Neur. Info. Proc. Sys. (NeurIPS), (2013) pp. 3111–-3119.
[6] B. Perozzi, R. Al-Rfou, S. Skiena. "Deepwalk: Online learning of social representations," Proceedings of the 20th ACM SIGKDD international conference on Knowledge Discovery and Data Mining (ACM) (2014), pp. 701–-710.
[7] J. Tang, M. Qu, M.Z. Wang, M. Zhang, J. Yan, Q.Z. Mei, "Line: Large-scale information network embedding," Proceedings of the 24th International Conference on World Wide Web (ACM) (2015) pp. 1067–-1077.
[8] A. Grover and J. Leskovec. "node2vec: Scalable feature learning for networks," Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (ACM) (2016).
[9] Z. Yang, W. Cohen, R. Salakhutdinov. "Revisiting semi-supervised learning with graph embeddings," Int. Conf. Mach. Learn. (ICML) (2016).
[10] Q. Lu and L. Getoor. "Link-based classification,", Int. Conf. Mach. Learn. (ICML) 3 (2003), pp. 496–-503.




