본 글에서는 DDPM(NeurIPS 2020)의 Markovian diffusion 구조로 인해 reverse sampling이 순차적 과정을 요구하는 한계를 살펴보고, 이를 non-Markovian inference 구조로 일반화하여 빠른 deterministic sampling을 가능하게 한 DDIM(ICLR 2021)을 살펴본다.
1. Introduction
DDPM의 generative process는 forward diffusion을 거꾸로 따라가는 구조다. 따라서 1) sampling에 수천 번의 sequential iteration 필요하고 2) 병렬화가 어렵다.
DDIM은 “Diffusion 모델의 샘플링을 더 빠르게 만들 수는 없을까?”의 문제 의식에서 출발한 논문이다. 이 논문은 DDPM은 Markovian forward diffusion을 사용하지만 학습에 실제로 필요한 것은 forward marginal 분포뿐이라는 점에서 forward를 꼭 Markov로 구성할 필요가 없다고 지적한다.
따라서 이 논문은 forward process를 non-Markovian으로 일반화하고, 그에 맞는 reverse generative chain을 설계한다. 즉 DDIM의 핵심은 forward process의 일반화를 통해 새로운 Generative process를 정의하면서, 학습 objective는 그대로 유지하고 기존 DDPM과 동일한 네트워크를 그대로 사용할 수 있다는 것이다.
결과적으로 forward process의 일반화 덕분에 1) generative Markov chain을 크게 단축할 수 있어 10×~100× 수준의 sampling 가속이 가능하며, 2) σ=0 설정을 통해 deterministic sampling이 가능해진다. 이 덕분에 3) 동일한 초기 latent에서 sampling step 수가 달라져도 high-level structure가 유지되는 consistency 성질을 확보할 수 있고 4) 초기 latent 간의 interpolation이 의미 있게 이어진다.
2. Background
논문의 해당 부분에서는 DDPM의 이해를 위한 기본적인 내용을 설명하고 있다.
(아래에는 DDIM 이해를 위해 중요한 부분만 간단히 정리해두었기 때문에 자세한 내용은 지난 DDPM 리뷰를 참고해주세요)
DDPM은 데이터 분포 \( q(x_0) \)를 근사하는 생성 모델로, forward diffusion과 reverse generative process로 구성된다.
Reverse Generative 과정은 다음과 같은 Markov chain 구조를 가진다.
$$
p_\theta(x_{0:T}) = p_\theta(x_T)\prod_{t=1}^{T} p_\theta(x_{t-1}\mid x_t)
$$
이 과정은 노이즈 \( x_T \)에서 시작하여 점진적으로 denoising을 수행하는 것이다.
Forward Diffusion 과정은 데이터를 점진적으로 Gaussian noise로 변환하는 Markov chain이다. 여기서 가장 중요한 성질은 다음 marginal 표현이다.
$$
x_t = \sqrt{\alpha_t}x_0 + \sqrt{1-\alpha_t}\epsilon,
\quad \epsilon \sim \mathcal{N}(0,I)
$$
이 식은 t 시점의 샘플이 원본과 노이즈의 선형 결합임을 의미한다. DDPM 학습은 이 구조를 이용해 각 시점의 노이즈 \( \epsilon \)을 예측하도록 모델을 학습한다.
$$
\min_\theta
\mathbb{E}_{x_0,\epsilon}
\left[
\|\epsilon_\theta(x_t) - \epsilon\|^2
\right]
$$
즉, DDPM은 본질적으로 noise prediction 모델이다.
3. Variational Inference for Non-Markovian Forward Processes
DDPM의 생성 과정은은 inference process의 reverse를 근사하므로, sampling 속도를 개선하려면 generative chain이 아니라 inference process 자체를 새롭게 설계할 필요가 있다.
이 논문의 핵심 관찰은 DDPM의 학습 목표가 각 시점의 marginal $q(x_t \mid x_0)$에만 의존한다는 점이다. 따라서 동일한 marginal을 유지하는 한, forward를 반드시 Markov 구조로 설계할 필요는 없으며, non-Markovian inference process로 일반화하더라도 DDPM과 동일한 surrogate objective로 학습할 수 있다는 것이 DDIM의 핵심 아이디어이다.

3.1 Non-Markovian Forward Processes
이 파트에서는 Markovian forward diffusion을 일반화하는 것을 설명한다. 핵심 아이디어는 동일한 marginal을 유지하면서, joint 구조를 새롭게 정의하는 것이다.

식 (6)은 새로운 inference joint 분포를 정의하는 식이다. 기존 DDPM에서는 $q(x_t \mid x_{t-1})$형태의 Markov chain을 사용했지만, 여기서는 $q_\sigma(x_{t-1} \mid x_t, x_0)$처럼 $x_0$까지 조건에 포함시킨다. 즉, forward joint를 Markov 구조에서 벗어나 non-Markovian 구조로 재정의하는 단계다.

식 (7)은 위에서 정의한 조건부 분포의 구체적인 Gaussian 형태를 제시한다. 평균은 모든 시점에서 marginal $q_\sigma(x_t \mid x_0) = \mathcal{N}(\sqrt{\alpha_t}x_0, (1-\alpha_t)I)$ 이 유지되도록 설계되어 있으며, 분산 $\sigma_t^2$ 는 stochasticity를 조절하는 자유 파라미터다. 즉, marginal은 고정하고 joint의 구조만 바꾸는 장치가 이 식이다.
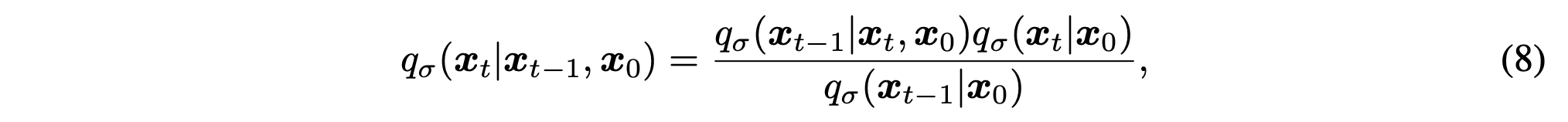
식 (8)은 Bayes rule을 통해 forward transition을 유도한 것이다. 이 식을 통해 정의된 forward 과정은 $x_t$ 가 $x_{t-1}$ 뿐 아니라 $x_0$ 에도 의존하게 되며, 따라서 더 이상 Markovian 구조가 아니다. 즉, 이 단계에서 forward diffusion은 non-Markovian으로 일반화된다.
➡️ 핵심은 DDPM의 forward는 Markov일 필요가 없으며, 동일한 marginal을 유지하는 non-Markovian joint를 설계할 수 있다는 것이다.
3.2 Generative Process and Unified Variational Inference Objective
이 파트에서는 앞서 정의한 non-Markovian forward process에 대응하는 generative process를 정의한다. 핵심은 noisy한 $x_t$가 주어지면, 먼저 원본 $x_0$을 예측하고, 그 예측값을 이용해 $x_{t-1}$을 계산하는 것이다.

식 (9)는 noisy한 $x_t$로부터 원본 $x_0$을 복원하는 식이다. 모델은 먼저 $x_t$에 포함된 노이즈 $\epsilon$을 예측하고, forward 식 $x_t = \sqrt{\alpha_t}x_0 + \sqrt{1-\alpha_t}\epsilon$을 역으로 정리하여 $x_0$의 추정값 $f_\theta^{(t)}(x_t)$을 계산한다. 즉, 이 식은 노이즈 예측을 원본 복원으로 연결하는 역할을 한다.
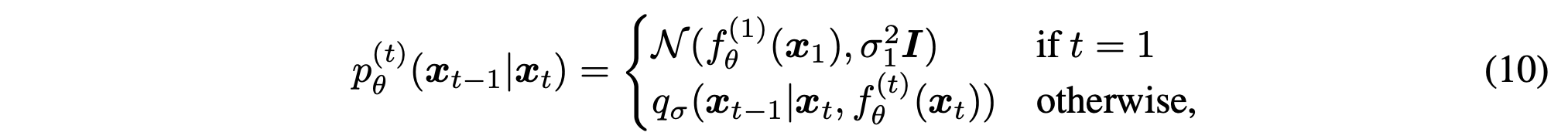
식 (10)은 복원된 $x_0$ 추정값을 이용해 $x_{t-1}$을 생성하는 generative transition을 정의한다. 여기서는 모델이 예측한 $f_\theta^{(t)}(x_t)$을 non-Markovian 조건부 $q_\sigma(x_{t-1} \mid x_t, x_0)$에 대입하여 reverse 과정을 구성한다. 즉, 이 식이 DDIM의 새로운 generative chain을 구체화하는 핵심 단계이다.
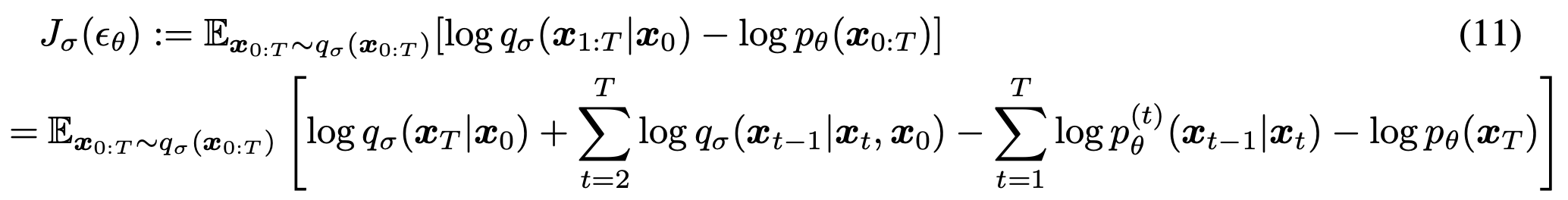
식 (11)은 위에서 정의한 generative process에 대응하는 변분 목적 함수이다. 표면적으로는 $\sigma$에 따라 다른 inference 분포와 generative chain이 정의되므로 다른 objective처럼 보이지만, 이후 Theorem 1에서 $J_\sigma = L_\gamma + C$ 임이 증명되며, 결과적으로 학습은 기존 DDPM의 noise prediction objective $L_\gamma$와 동일하게 유지된다.
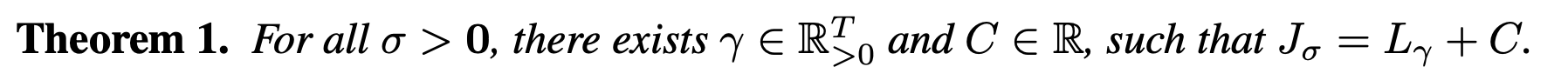
Theorem 1의 핵심은, 앞서 정의한 variational objective $J_\sigma(\epsilon_\theta)$가 특정 가중치 $\gamma$와 상수 $C$에 대해 $J_\sigma = L_\gamma + C$로 표현될 수 있다는 점이다. 즉, non-Markovian forward를 사용해 새롭게 정의한 generative process에 대응하는 objective 역시, DDPM에서 사용하는 noise prediction objective $L_\gamma$와 본질적으로 동치라는 의미다. 특히 모델의 각 시점별 파라미터 $\epsilon_\theta^{(t)}$가 서로 공유되지 않는다면, $L_\gamma$의 최적해는 가중치 $\gamma$에 의존하지 않으며, 결과적으로 $J_\sigma$의 최적해 또한 기존 DDPM에서 사용하는 $L_1$ objective와 동일해진다. 이는 forward 구조를 일반화하더라도 학습 자체는 기존 DDPM과 완전히 동일하게 수행할 수 있음을 보장한다.
➡️ 핵심은 모델은 여전히 노이즈를 예측하고, 그 예측을 통해 $x_0$을 복원하며 복원값을 이용해 새로운 generative chain을 정의하는데 이 때 학습 objective는 DDPM과 동일하다는 것이다. 이 덕분에 DDIM은 DDPM에서 학습된 네트워크를 그대로 사용할 수 있다.
4. Sampling from Generalized Generative Processes
$L_1$ objective로 학습된 모델은 단지 Markovian forward에 대응하는 generative process만 학습하는 것이 아니라, 앞서 정의한 $\sigma$로 파라미터화된 다양한 non-Markovian forward process에 대해서도 동시에 해를 제공한다. 즉, 기존에 학습된 DDPM 모델을 그대로 사용하면서도, $\sigma$ 값을 조절함으로써 서로 다른 generative process를 선택할 수 있다. 따라서 DDIM의 핵심은 새로운 모델을 다시 학습하는 것이 아니라, 이미 학습된 DDPM을 기반으로 $\sigma$를 조정하여 목적에 맞는 sampling 방식을 구성하는 데 있다.
4.1 Denoising Diffusion Implicit Models
이 파트는 generative process를 실제 sampling 식으로 구체화하고, $\sigma$ 선택에 따라 서로 다른 생성 모델을 얻을 수 있음을 보인다.
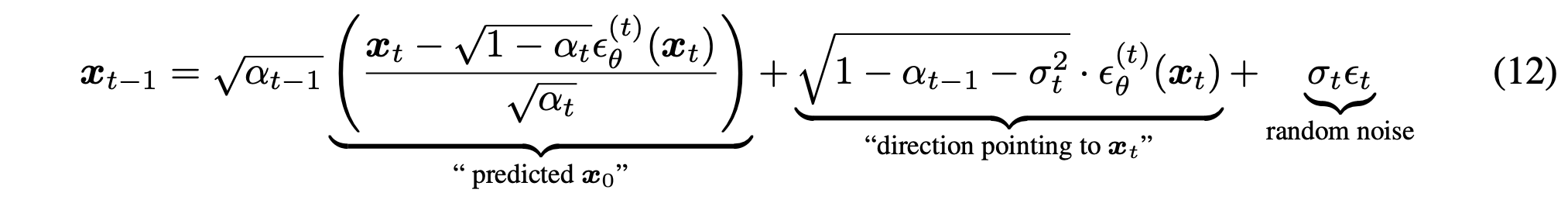
식 (12)는 모델이 예측한 노이즈 $\epsilon_\theta^{(t)}(x_t)$를 통해 먼저 $x_0$을 추정한 뒤, 이를 이용해 $x_{t-1}$을 계산하는 update 식이다.
여기서 $\sigma_t$는 reverse 과정에 추가되는 랜덤성의 크기를 조절하며, 동일한 네트워크 $\epsilon_\theta$를 사용하면서도 $\sigma_t$ 값에 따라 서로 다른 generative process를 구성할 수 있다. 특정한 $\sigma_t$를 선택하면 기존 DDPM과 동일한 Markovian sampling이 되고, 반대로 모든 $t$에 대해 $\sigma_t = 0$이면 reverse 과정이 완전히 deterministic해진다. 이 경우 sampling은 고정된 $x_T$에서 시작해 정해진 경로를 따라 $x_0$으로 이동하는 implicit probabilistic model이 되며, 이를 denoising diffusion implicit model(DDIM)이라 정의한다.
4.2 Accelerated Generation Processes
이 파트의 핵심은 generative process를 반드시 전체 $T$ step에 대해 수행할 필요가 없다는 점이다.
DDPM에서는 forward가 $T$ step이므로 reverse도 $T$ step을 모두 따라가야 했지만, 학습 objective $L_1$은 오직 marginal $q_\sigma(x_t \mid x_0)$에만 의존하므로 forward의 모든 중간 변수들을 반드시 사용할 필요는 없다. 따라서 $x_{1:T}$ 전체가 아니라 부분 집합 ${x_{\tau_1}, \dots, x_{\tau_S}}$에 대해서만 forward를 정의하고, reverse 과정도 그에 대응하는 trajectory에 대해서만 수행할 수 있다.
이때 각 시점은 여전히 $q(x_{\tau_i} \mid x_0) = \mathcal{N}(\sqrt{\alpha_{\tau_i}}x_0, (1-\alpha_{\tau_i})I)$를 만족하도록 유지된다. Sampling trajectory의 길이 $S$가 $T$보다 훨씬 작으면 iterative한 generative process의 계산량이 크게 줄어들며, 학습을 다시 할 필요 없이 기존 $L_1$로 학습된 모델을 그대로 사용할 수 있다.
즉, forward는 길게 학습하되, sampling은 일부 step만 선택해 수행함으로써 효율을 크게 향상시킬 수 있다는 것이 핵심이다.
4.3 Relevance to Neural ODEs
이 파트의 핵심은 DDIM의 업데이트 식이 ordinary differential equation(ODE)의 Euler 근사와 유사하다는 점이다.
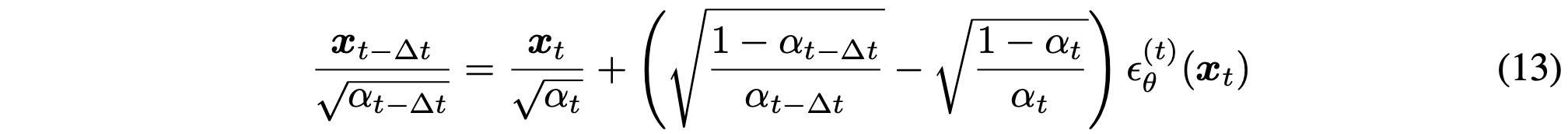

식 (13)은 DDIM의 discrete update를 재정리한 것으로, 이를 적절히 재파라미터화하면 연속 시간에서의 미분 방정식 형태인 ODE (식 (14))로 해석할 수 있다. 즉, DDIM의 deterministic sampling은 사실상 특정 ODE를 Euler 방식으로 적분하는 과정과 동일하다.
이는 충분히 많은 discretization step을 사용하면 생성 과정을 역방향뿐 아니라 정방향으로도 수행할 수 있음을 의미하며, DDIM을 통해 관측 데이터를 latent $x_T$로 인코딩하는 것이 가능해진다.
또한 논문은 이 ODE가 Song et al. (2020)의 probability flow ODE의 특수한 경우와 동치임을 보이며, 다만 두 방법은 Euler step을 취하는 기준이 다르기 때문에 sampling step 수가 적을 경우 업데이트 결과에 차이가 발생할 수 있음을 지적한다. 결국 이 섹션은 DDIM이 단순한 heuristic 가속 기법이 아니라, 연속시간 ODE 관점에서 정당화될 수 있는 구조임을 보여준다.
5. Experiments
실험에서는 모든 데이터셋에 대해 동일한 사전 학습된 DDPM 모델($T=1000$, objective는 $L_\gamma$ with $\gamma=1$)을 그대로 사용하며, 학습 과정은 전혀 변경하지 않는다.
sampling 단계에서만 부분 수열 $\tau \subset \{1,\dots,T\}$를 선택해 생성 trajectory 길이를 줄이고, 분산 하이퍼파라미터 $\sigma$를 $\eta$로 조절한다. 구체적으로
$\sigma_{\tau_i}(\eta)=\eta\sqrt{\frac{1-\alpha_{\tau_i-1}}{1-\alpha_{\tau_i}}\cdot\frac{1-\alpha_{\tau_i}}{\alpha_{\tau_i-1}}}$
로 정의하며, $\eta=1$이면 기존 DDPM sampling, $\eta=0$이면 deterministic DDIM sampling이 된다. 즉, 동일한 네트워크 $\epsilon_\theta$를 유지한 채 sampling trajectory $\tau$와 stochasticity $\eta$만 조절하여 DDPM과 DDIM을 하나의 연속적인 generative family로 비교한 것이 실험의 핵심 세팅이다.
5.1 Sample Quality and Efficiency

Table 1의 결과에 따르면, sampling step 수 $\mathrm{dim}(\tau)$가 증가할수록 FID는 개선되지만 계산 비용 역시 선형적으로 증가한다는 trade-off가 확인된다. 중요한 점은 적은 step 영역에서 $\eta=0$인 DDIM이 가장 안정적으로 낮은 FID를 달성한다는 것이다. 특히 20~100 step만으로도 1000 step DDPM과 유사한 품질을 보이며, 이는 약 10×~50× 수준의 속도 향상에 해당한다.

반면 $\eta=1$인 DDPM과 $\hat{\sigma}$ 설정은 step 수가 줄어들수록 품질이 급격히 악화되며, 이는 Figure 3에서 시각적으로도 확인된다.

또한 Figure 4는 sampling 시간이 trajectory 길이에 선형적으로 비례함을 보여주며, DDIM이 적은 step에서 높은 품질을 유지함으로써 실질적인 효율 개선을 제공함을 뒷받침한다.
5.2 Sample Consistency in DDIMs

Figure 5는 DDIM의 가장 중요한 특성인 consistency를 보여준다. DDIM은 deterministic generative process이므로 $x_0$는 오직 초기 latent $x_T$에 의해 결정된다. 실제로 동일한 $x_T$에서 서로 다른 generative trajectory $\tau$를 사용해도 생성된 이미지의 high-level 구조는 거의 동일하게 유지된다.
특히 20 step만 사용한 경우에도 1000 step 생성 결과와 의미적 구조는 매우 유사하며, 차이는 주로 세부 디테일 수준에서 나타난다. 이는 $x_T$가 이미지의 의미 정보를 담고 있는 informative latent encoding 역할을 한다는 것을 시사하며, sampling step 수 증가는 주로 세부 품질 개선에 기여할 뿐 high-level semantics를 크게 바꾸지는 않는다는 점을 보여준다.
5.3 Interpolation in Deterministic Generative Processes

Figure 6은 DDIM이 latent space에서 의미 있는 interpolation을 수행할 수 있음을 보여준다. DDIM에서는 high-level semantic 정보가 초기 latent $x_T$에 인코딩되어 있으므로, 두 latent 사이를 선형 보간하면 생성 이미지 역시 자연스럽게 의미적으로 변화한다.
이는 stochastic generative process를 사용하는 DDPM과 대비되는 특성으로, DDPM에서는 동일한 $x_T$에서도 다양한 $x_0$가 생성되기 때문에 이러한 일관된 interpolation이 어렵다. 따라서 DDIM은 latent 변수 $x_T$를 직접 조작함으로써 생성 결과의 high-level 구조를 제어할 수 있는 implicit generative model의 성질을 가진다.
5.4 Reconstruction from Latent Space
논문은 DDIM이 ODE 기반 구조라는 점을 활용해, $x_0 \rightarrow x_T$로 encoding한 뒤 다시 $x_T \rightarrow x_0$로 decoding하여 복원이 가능한지를 실험했다.

CIFAR-10 테스트셋에서 동일한 step 수 $S$로 인코딩과 디코딩을 수행한 결과, $S$가 클수록 reconstruction error(MSE)가 감소하는 경향을 보였다. 이는 DDIM이 Neural ODE나 normalizing flow처럼 비교적 안정적인 invertible 특성을 가진다는 것을 시사한다. 반면 DDPM은 generative 과정이 stochastic하기 때문에 동일한 방식의 정확한 복원이 어렵다.
6. Related Work
이 논문은 Markov chain 기반 generative 모델 계열 위에 있다. 특히 DDPM과 NCSN은 여러 noise level에서 denoising objective를 학습하고, Langevin dynamics 기반 iterative sampling을 수행한다는 공통점이 있다. 이 방법들은 높은 샘플 품질을 달성했지만, Langevin dynamics 자체가 gradient flow의 이산화이기 때문에 많은 step이 필요하다는 구조적 한계를 가진다.
반면 DDIM은 implicit generative model로 해석되며, latent가 주어지면 샘플이 거의 결정적으로 정해진다. 이 특성은 GAN이나 normalizing flow처럼 의미 있는 interpolation이 가능하다는 점에서 유사성을 가진다. 또한 DDIM은 Langevin dynamics의 제약에서 벗어나 variational 관점에서 유도되었기 때문에, 적은 step에서도 DDPM보다 더 나은 품질을 보일 수 있다. Sampling 방식은 Neural ODE와도 유사한 구조를 가진다.
7. Discussion
이 논문은 DDIM을 variational 관점에서 정식화된 implicit generative model로 제시한다. DDIM은 기존 DDPM보다 훨씬 적은 step으로 고품질 샘플을 생성할 수 있으며, latent space에서 의미 있는 interpolation이 가능하다는 점에서 기존 diffusion 모델과 차별화된다.
또한 논문은 non-Markovian forward process가 Gaussian에만 제한될 필요가 없음을 시사한다. 기존 diffusion framework에서는 안정성 문제로 사실상 Gaussian만 사용 가능했지만, DDIM의 관점에서는 다른 연속적 혹은 이산적 구조로의 확장 가능성이 생긴다.
마지막으로 DDIM sampling이 Neural ODE와 유사한 구조를 가지는 만큼, ODE 해석에서 사용하는 고차 적분 기법을 적용하면 더 적은 step으로 품질을 개선할 가능성도 제안한다. 즉, DDIM은 단순한 가속 기법을 넘어, diffusion 모델을 implicit model 및 연속시간 관점으로 확장하는 출발점이라는 의미를 가진다.
