[DDIM] https://arxiv.org/abs/2010.02502
Denoising Diffusion Implicit Models
Denoising diffusion probabilistic models (DDPMs) have achieved high quality image generation without adversarial training, yet they require simulating a Markov chain for many steps to produce a sample. To accelerate sampling, we present denoising diffusion
arxiv.org
본 논문은 Denoising Diffusion Probabilistic Models(DDPM)와 깊은 연관이 있으므로 해당 논문을 읽지 않았다면 이해가 힘들 수 있다.
[DDPM 논문리뷰] https://outta.tistory.com/181
[2025-1] 최민서 - Denoising Diffusion Probabilistic Models
[DDPM] https://arxiv.org/abs/2006.11239 Denoising Diffusion Probabilistic ModelsWe present high quality image synthesis results using diffusion probabilistic models, a class of latent variable models inspired by considerations from nonequilibrium thermody
blog.outta.ai
1. Introduction
DDPM(Denoising Diffusion Probabilistic Models)은 학습이 쉽고 샘플링 성능이 좋다는 장점이 있지만, 샘플링 과정이 일반적으로 $1000$ step 가까이로 구성되어 샘플링하는데 매우 오랜 시간이 걸린다. 이를 해결하기 위해 본 논문에서는 DDIM(Denoising Diffusion Implicit Models)을 소개한다.
DDIM은 DDPM과 같은 모델, 같은 학습방식을 사용하지만 기존 forward diffusion process를 non-Markovian하게 변형하여 샘플링 과정을 간소화한다. 이로써 DDPM에서 샘플링 과정만 발전시킨 DDIM은 아래 세 가지 이점을 가진다.
- DDIM은 DDPM보다 짧은 시간에 DDPM보다 좋은 품질의 이미지를 생성한다.
- DDIM은 'consistency' 특성을 가진다.
이는 동일한 latent variable을 갖고 샘플을 생성하면 동일한 이미지 샘플들이 생성된다는 의미이다.
- 'consistent'한 DDIM은 초기 latent variable 조작을 통한 의미있는 interpolation을 수행할 수 있다.
2. Background
본 섹션에서는 Diffusion Model과 관련있는 기본적인 수식들을 정리한다.
이는 DDPM 논문에서의 정의와 같다. 다만 DDPM 논문에서는 $\beta_t$를 정의한 후 이를 통해 $\alpha_t$와 $\bar{\alpha}_t$를 정의했는데, 본 논문에서는 그냥 $\alpha_t$를 $0$으로 감소하는 수열이라 정의했다. 본 논문의 $\alpha_t$를 DDPM 논문의 $\bar{\alpha}_t$라 생각하면 된다.
숙지해야할 주요 사항은 아래와 같다.
forward process는 Markov chain으로 구성된다. 이 때 $x_t$와 $x_0$의 조건부 확률분포는 아래와 같다.
$$ q(x_t|x_0) := \int q(x_{1:t}|x_0)dx_{1:(t-1)} = \mathcal{N}(x_t; \sqrt{\alpha_t}x_0, (1-\alpha_t)\mathbf{I}) $$
즉 $x_t$를 아래와 같이 $x_0$와 노이즈 $\epsilon$의 선형 결합으로 표현할 수 있다. 이 때 $alpha_t$는 $alpha_T$가 $0$에 충분히 가까운 감소하는 수열이다.
$$ x_t = \sqrt{\alpha_t}x_0 + \sqrt{1-\alpha_t}\epsilon, \; \text{where} \; \epsilon \sim \mathcal{N}(0,\mathbf{I}) $$
Variational lower bound는 아래와 같이 정의된다.
$$ \max\limits_\theta \mathbb{E}_{q(x_0)}[\mathrm{log}p_\theta(x_0)] \leq \max\limits_\theta \mathbb{E}_{q(x_0,x_1,...,x_T)}[\mathrm{log}p_\theta(x_{0:T}) - \mathrm{log}q(x_{1:T}|x_0)] $$
모든 조건이 가우시안 분포로 설정되어 있고, 학습 가능한 평균과 고정된 분산으로 위 VLB를 아래와 같이 단순화할 수 있다.
이는 DDPM 논문의 주요 내용이다.
$$ L_\gamma(\epsilon_\theta) := \sum\limits_{t=1}^{T} \gamma_t\mathbb{E}_{x_0\sim q(x_0),\epsilon_t\sim\mathcal{N}(0,\mathbf{I})} \left[ \Vert \epsilon_\theta^{(t)}( \sqrt{\alpha_t}x_0 + \sqrt{1-\alpha_t}\epsilon_t ) - \epsilon_t \Vert_2^2 \right] $$
DDPM 논문에서는 $\gamma=\mathbf{1}$로 설정하고 학습시킨 후 $x_T$로부터 $x_0$를 $T$ step에 걸쳐 샘플링했다. DDPM에서 time step $T$는 중요한 hyperparameter이다. 실제로 $T=1000$으로 설정되는데 이는 정교한 샘플을 생성하는데에 기여하지만 그만큼 필요한 step의 수가 길어져 샘플링 시 많은 자원이 소모된다는 단점이 있다.
3. Variational Inference for Non-Markovian Forward Processes
본 섹션에서는 DDIM의 샘플링 방식을 구현하기 위한 수학적 기반을 다진다.
어떻게 샘플링을 하는지는 section 4에 나온다. 여기서는 forward 및 reverse process만 새롭게 정의한다.
DDPM의 목적함수인 $L_\gamma$는 marginal distributions $q(x_t|x_0)$에만 의존하고, joint distribution $q(x_{1:T}|x_0)$에는 직접적으로 의존하지 않는다. 같은 marginal distribution을 가지는 joint distribution은 하나 이상 존재할 수 있다.
본 논문에서는 joint distribution $q(x_{1:T}|x_0)$를 대신할 joint distribution을 찾는다. 두 joint distribution이 서로 다른 형태이더라도, 그것들의 marginal distirbution들이 같다면 두 reverse process의 목적함수 $L_\gamma$ 값은 동일할 것이고, 따라서 DDPM과 동일한 모델을 사용하고 동일한 방식으로 학습시킬 수 있다. 특히 본 논문에서는 forward 및 reverse process를 non-Markovian kernel들로 구성한다.
3.1 Non-Markovian Forward Processes
joint distribution $q_\sigma(x_{1:T}|x_0)$은 아래와 같이 정의된다.
$$ q_\sigma(x_{1:T}|x_0) := q_\sigma(x_T|x_0)\prod\limits_{t=2}^Tq_\sigma(x_{t-1}|x_t,x_0) $$
$T$차원의 실수 벡터 $\sigma$에 대해 non-Markovian kernel $q_\sigma(x_{t-1}|x_t,x_0)$를 $t>1$에서 아래와 같이 정의한다.
$$ q_\sigma(x_{t-1}|x_t,x_0) = \mathcal{N}\left( \sqrt{\alpha_{t-1}}x_0 + \sqrt{1-\alpha_{t-1}-\sigma_t^2} \cdot \frac{x_t-\sqrt{\alpha_t}x_0}{\sqrt{1-\alpha_t}}, \sigma_t^2\mathbf{I} \right) $$
위 조건부 확률분포의 평균은 모든 $t$에 대하여 $q_\sigma(x_t|x_0) = \mathcal{N}(\sqrt{\alpha_t}x_0,(1-\alpha_t)\mathbf{I})$를 만족하도록 설정되었다.
Forward process의 각 kernel들은 아래와 같이 non-Markovian하게 정의된다. Bayes' rule을 통해 유도할 수 있다.
$$ q_\sigma(x_t|x_{t-1},x_0) = \frac{q_\sigma(x_{t-1}|x_t,x_0)q_\sigma(x_t|x_0)}{q_\sigma(x_{t-1}|x_0)} $$
3.2 Generative Process and Unified Variational Inference Objective
3.1에서 forward process $q_\sigma$를 non-Markovian하게 정의했다. 이제 $q_\sigma(x_{t-1}|x_t,x_0)$을 이용하여 reverse kernel $p_\theta^{(t)}(x_{t-1}|x_t)$을 구성해보자.
DDPM에서 쓰이는 모델 $\epsilon_\theta^{(t)}$를 그대로 사용한다. 해당 모델은 노이즈 있는 이미지 $x_t$에 있는 노이즈의 값을 추정한다. 이 값을 통해 $x_0$에 대한 예측값을 아래와 같이 나타낼 수 있다.
$$f_\theta^{(t)}(x_t) := \frac{(x_t-\sqrt{1-\alpha_t}\cdot\epsilon_\theta^{(t)}(x_t))}{\sqrt{\alpha_t}}$$
이제 고정된 초기 분포 $p_\theta(x_T) = \mathcal{N}(0,\mathbf{I})$에 대하여 generative process를 아래와 같이 나타낼 수 있다.
$$ p_\theta^{(t)}(x_{t-1}|x_t) = \begin{cases} \mathcal{N}(f_\theta^{(1)}(x_1),\sigma_1^2\mathbf{I}) & \text{if}\; t=1 \\ q_\sigma(x_{t-1}|x_t,f_\theta^{(t)}(x_t)) & \text{otherwise} \end{cases} $$
$q_\sigma(x_{t-1}|x_t,x_0)$의 $x_0$가 $f_\theta^{(t)}(x_t)$가 $x_0$로 대체되었다고 생각하면 된다.
아래의 VLB를 이용하여 $\theta$를 최적화한다.
$ J_\sigma(\epsilon_\theta) := \mathbb{E}_{x_{0:T}\sim q_\sigma(x_{0:T})} [ \mathrm{log}q_\sigma(x_{1:T}|x_0) - \mathrm{log}p_\theta(x_{0:T}) ] $
$$= \mathbb{E}_{x_{0:T}\sim q_\sigma(x_{0:T})} \left[ \mathrm{log}q_\sigma(x_T|x_0) + \sum\limits_{t=2}^T\mathrm{log}q_\sigma(x_{t-1}|x_t,x_0) - \sum\limits_{t=1}^T\mathrm{log}p_\theta^{(t)}(x_{t-1}|x_t) - \mathrm{log}p_\theta(x_T) \right] $$
$\sigma$의 값에 따라 VLB 값이 달라지기 때문에 학습이 어려울 수 있지만, 아래에서 볼 수 있듯이, $J_\sigma$는 특정 $\gamma$에 대해 $L_\gamma$와 같다.
이에 대한 증명은 논문의 Appendix B에 있다.
$$ \text{Theroem 1. For all} \; \sigma>\mathbf{0}, \; \text{there exists} \; \gamma \in \mathbb{R}_{>0}^T \; \text{and} \; C \in \mathbb{R},\; \text{such that} \; J_\sigma = L_\gamma + C$$
모델 $\epsilon_\theta^{(t)}$는 $t$의 값에 따라 파라미터가 달라진다. 그렇기 때문에 최적화된 매개변수 $\theta$는 $\gamma$에 의존하지 않는다.
어차피 $L_\gamma$를 최적화하려면 모든 시점 $t$에서 $L$ 값을 최적화하여야 하기 때문에 계수 $\gamma$는 $L_\gamma$의 최적화에 영향을 미치지 않는다.
따라서 $J_\sigma$를 최적화하는 것은, 특정 $\gamma$에 대해 $L_\gamma$를 최적화하는 것과 같고, 이는 $L_\mathbf{1}$을 최적화 하는 것과 같다. 결국 $J_\sigma$를 최적화하는 대신, DDPM과 같은 방식으로 학습을 시켜주면 된다.
Section 3의 내용을 요약하면 아래와 같다.
- non-Markovian kernel $q_\sigma$와 $p_\theta^{(t)}$는 아래와 같이 정의된다.
$$ q_\sigma(x_{t-1}|x_t,x_0) = \mathcal{N}\left( \sqrt{\alpha_{t-1}}x_0 + \sqrt{1-\alpha_{t-1}-\sigma_t^2} \cdot \frac{x_t-\sqrt{\alpha_t}x_0}{\sqrt{1-\alpha_t}}, \sigma_t^2\mathbf{I} \right) $$
$$ p_\theta^{(t)}(x_{t-1}|x_t) = \begin{cases} \mathcal{N}(f_\theta^{(1)}(x_1),\sigma_1^2\mathbf{I}) & \text{if}\; t=1 \\ q_\sigma(x_{t-1}|x_t,f_\theta^{(t)}(x_t)) & \text{otherwise} \end{cases} $$
- 위와 같이 forward 및 reverse process를 정의하더라도 모델의 구축 및 학습 과정은 DDPM과 동일하다.
4. Sampling from Generalized Generative Processes
Section 3에서 확인했듯이, $q_\sigma$를 활용해도 같은 목적함수를 갖기 때문에 결국 학습된 DDPM 모델을 사용하면 된다. Section 4에서는 파라미터 $\sigma$를 변형하여 샘플링 과정을 간소화시킬 방법을 찾는다.
4.1 Denoising Diffusion Implicit Models
Section 3에서 정의한 $p_\theta^{(t)}$를 이용하여 $x_{t-1}$을 $x_t$로부터 아래와 같이 샘플링할 수 있다.
$$ x_{t-1} = \sqrt{\alpha_{t-1}} \underbrace{\left( \frac{x_t - \sqrt{1-\alpha_t}\epsilon_\theta^{(t)}(x_t)}{\sqrt{\alpha_t}} \right)} _{\text{"predicted} \; x_0\text{"}} + \underbrace{\sqrt{1-\alpha_{t-1}-\sigma_t^2}\cdot\epsilon_\theta^{(t)}(x_t)}_{\text{"direction pointing to} \; x_t \text{"}} + \underbrace{\sigma_t\epsilon_t}_{\text{random noise}} $$
$\epsilon_t$는 표준정규분포 노이즈이고, $\alpha_0:=1$이라 정의한다.
$\sigma_t = \sqrt{(1-\alpha_{t-1})/(1-\alpha_t)}\sqrt{1-\alpha_t/\alpha_{t-1}}$이라 설정하면 forward process는 Markovian이 되고, 샘플링 과정은 DDPM과 같게 된다.
DDIM(Denoising Diffusion Implicit Models)에서는 $\sigma_t=0$이라 설정한다. 샘플링 과정에서 latent variable $x_T$가 생성되면 $x_0$가 결정론적으로 생성된다.
결정론적 과정(deterministic process)이란 처음 데이터가 생성된 시점에서 최종적인 데이터의 값이 결정되었다는 의미이다. 이는 데이터 변형 과정 중 랜덤성이 전혀 없기에 가능하다.
4.2 Accelerated Generation Processes
DDPM에서 forward process와 reverse process는 $T$ step으로 구성된다. 하지만 $q_\sigma(x_t|x_0)$만 고정되어 있다면 다른 forward process를 들여와도 목적함수 $L_1$에는 영향을 끼치지 않는다. 따라서 본 섹션에서는 $T$보다 작은 값으로 reverse process를 구성하여 샘플링하는데에 들이는 시간과 비용을 절감한다.
$\tau$를 길이 $S$의 $[1,\dots,T]$의 증가하는 부분수열이라 정의하자. $\{x_{\tau_1},\dots,x_{\tau_S}\}$는 latent variables $\{x_{1:T}\}$의 부분집합이고 forward 및 reverse process는 해당 부분집합에서 아래와 같이 정의된다.
$$ q_{\sigma,\tau}(x_{\tau_{i-1}}|x_\tau,x_0) = \mathcal{N}\left( \sqrt{\alpha_{\tau_{i-1}}}x_0 + \sqrt{ 1-\alpha_{\tau_{i-1}}-\sigma_{\tau_i}^2 }\cdot\frac{x_{\tau_i} - \sqrt{\alpha_{\tau_i}}x_0}{1-\alpha_{\tau_i}}, \sigma_{\tau_i}^2\mathbf{I} \right) $$
$$ p_\theta^{(\tau_i)}(x_{\tau_{i-1}}|x_{\tau_i}) = \begin{cases} q_{\sigma,\tau}(x_{\tau_{i-1}} | x_{\tau_i},f_\theta^{(\tau_i)}(x_{\tau_{i-1}})) &\text{if}\; i=1 \\ \mathcal{N}(f_\theta^{(t)}(x_t),\sigma_t^2\mathbf{I}) &\text{otherwise}\end{cases} $$
위와 같이 정의했을 때, 계산을 해보면 $q(x_{\tau_i}|x_0)=\mathcal{N}(\sqrt{\alpha_{\tau_i}}x_0,(1-\alpha_{\tau_i})\mathbf{I})$를 만족시키는 것을 확인할 수 있다. 즉 $S$개의 latent variables로 구성된 집합에서 정의된 샘플링 방식도 $L_1$으로 학습된 DDPM 모델을 이용할 수 있다.
엄밀한 수학적 정의 및 marginal distribution에 대한 증명은 논문의 Appendix C.1를 참고하면 된다. 해당 부분에서 $\tau$를 제외한 변수들에서의 forward 및 reverse process가 정의된다. 이들은 실제 샘플링 과정에서는 쓰이지 않지만, 이론을 구축하는데에 있어서 수학적으로 큰 도움을 준다.
만약 $S$의 크기를 충분히 작게 할 수 있다면 이는 샘플링 속도 향상에 크게 영향을 끼친다. 이에 따라 step의 수 $T$를 늘릴 수 있고 심지어 시간 변수 $t$를 연속적으로 설정할 수도 있다. 이에 대해서 논문에서 다루지는 않는다.
Section 4.1과 4.2의 내용을 보면, DDIM은 아래의 두가지 변형을 통해 이미지를 효율적으로 샘플링한다.
- $\sigma_t=0$으로 설정하여 결정론적으로 이미지를 샘플링한다.
- 수열 $\{1,\dots,T\}$의 부분수열에서 reverse process를 정의하여 샘플링 과정을 간소화한다.
4.3 Relevance to Neural ODEs
DDIM의 샘플링 step은 아래와 같다.
$$ x_{t-1} = \sqrt{\alpha_{t-1}}\left( \frac{x_t-\sqrt{1-\alpha_t}\epsilon_\theta^{(t)}(x_t)}{\sqrt{\alpha_t}} \right) + \sqrt{1-\alpha_{t-1}}\cdot \epsilon_\theta^{(t)}(x_t) $$
위 수식은 ordinary differential equation(ODE)를 푸는 오일러 적분 방식과 그 형태가 유사하다. 아래와 같이 나타내면 이는 더 명확해진다.
$$ \frac{x_{t-\Delta t}}{\sqrt{\alpha_{t-\Delta t}}} = \frac{x_t}{\sqrt{\alpha_t}} + \left( \sqrt{\frac{1-\alpha_{t-\Delta t}}{\alpha_{t-\Delta t}}} - \sqrt{\frac{1-\alpha_t}{\alpha_t}} \right) \epsilon_\theta^{(t)}(x_t) $$
위 수식에서 $\frac{\sqrt{1-\alpha}}{\sqrt{\alpha}}$를 $\sigma$로, $\frac{x}{\sqrt{\alpha}}$를 $\bar{x}$로 매개화하여 정리하면, 위 수식은 아래의 ODE를 푸는 오일러 적분 식이다.
$$ d\bar{x}(t) = \epsilon_\theta^{(t)}\left( \frac{\bar{x}(t)}{\sqrt{\sigma^2+1}} \right)d\sigma(t) $$
즉 DDIM의 샘플링 step은 연속적인 $t$에 대하여 위 ODE를 푸는 적분 식이라 생각할 수 있으며 이 과정을 역으로 계산하면 $x_0$로부터 $x_T$를 구하는 인코딩 과정도 설명할 수 있다.
5. Experiments
본 섹션에서는 DDPM과 DDIM의 성능을 비교한다. Section 4에서 논의한 $\sigma$의 값과 $\tau$의 길이를 바꾸어가며 성능을 측정한다. 이 때 동일하게 학습된 동일한 모델을 사용하고 샘플링 방식에만 차이를 둔다.
$\sigma$는 아래와 같이 설정된다.
$$ \sigma_{\tau_i}(\eta) = \eta\sqrt{\frac{1-\alpha_{\tau_{i-1}}}{1-\alpha_{\tau_i}}}\sqrt{\frac{1-\alpha_{\tau_i}}{\alpha_{\tau_{i-1}}}} $$
$\eta$는 직접 조절 가능한 변수이며 $\eta=1$일 땐 DDPM, $\eta=0$일 땐 DDIM이다.
5.1 Sample Quality and Efficiency
아래 표는 $\tau$의 길이와 $\sigma$의 값에 따른 성능 측정 결과이다. $\hat{\sigma}$는 DDPM 논문 구현에서 CIFAR10 샘플들을 생성할 때 쓰이는 특별한 $\sigma$ 값이다.

$S$의 값이 $1000$일 때는 DDPM의 성능이 미세하게 더 좋지만, $S$의 크기가 작아질수록 DDIM의 성능이 훨씬 좋음을 확인할 수 있다. 특히 샘플링 과정을 $10$~$50$배 줄여도 DDIM의 성능은 크게 줄어들지 않는다.
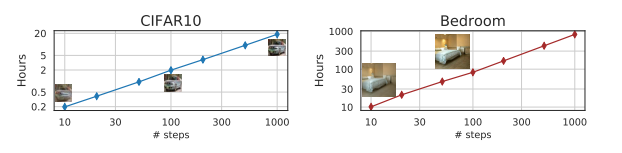
위 그래프에서 확인할 수 있듯이 $S$의 값, 즉 step의 수가 줄어듦에 따라 샘플링하는데 걸리는 시간도 이에 비례해서 줄어듦을 확인할 수 있다. DDIM을 사용하면 샘플링 성능의 큰 손해 없이 샘플링 시간을 크게 줄일 수 있다.
5.2 Sample Consistency in DDIMs
DDIM은 결정론적 방식으로 샘플을 생성하기 때문에 latent variable $x_T$에 따라 단 하나의 $x_0$가 결정된다. 아래 그림에서는 $\tau$의 길이를 다르게 하여 같은 $x_T$로부터 생성한 샘플들이다.

$\tau$의 길이를 다르게 해도 이미지의 주요한 큰 특징들은 동일하고, 세부적인 디테일들만 달라짐을 확인할 수 있다. 즉 latent variable $x_T$에 이미지의 큰 특징들의 정보가 담겨있고, 세부적인 정보는 모델의 파라미터에 담겨있다고 추론할 수 있다.
5.3 Interpolation in Deterministic Generative Processes
아래 그림은 $\tau$의 길이가 $50$일 때 interpolation 결과이다. 두 서로 다른 latent variable $x_T$가 interpolate 되어 이미지를 생성하였다.

위 그림에서 볼 수 있듯이, 상위 단계인 $x_T$에서 interpolation이 이루어져도 직관적으로 의미있는 방식으로 두 이미지가 interpolate 되었음을 확인할 수 있다. 이는 DDPM에서는 볼 수 없는 특성으로 DDIM에서 latent variable $x_T$가 이미지의 주요 특징에 대한 정보를 담고 있기 때문에 나타난 결과이다.
5.4 Reconstruction from Latent Space
section 4.3에서 DDIM을 특정 ODE의 오일러 적분 풀이임을 보였다. 해당 neural ODE 식을 통해 $x_0$로부터 $x_T$를 생성하고 다시 이로부터 $x_0$를 생성하는 reconstruction을 진행하고 이 때의 오차를 MSE로 계산해보니 아래와 같이 나타났다.

오일러 풀이 방식은 $t$가 연속적이라 가정한다. 따라서 이산적인 step이 촘촘할수록 오차가 작아질 것이고 이는 step의 길이 $S$가 커질수록 오차가 작아지는 실험결과와 일맥상통한다.
6. Conclusion
본 논문에서는 DDPM 모델의 샘플링 방식을 변형하여 DDIM 모델을 정립했다. 이는 학습된 모델을 통해 결정론적으로 이미지를 샘플링하는 방식으로 기존 DDPM 샘플링 방식보다 $20$~$50$배 빠른 속도와 준수한 성능을 보여주었다. 또한 latent variable $x_T$에 이미지 $x_0$에 대한 주요한 특징이 담겨있고, 이로 인해 latent variable을 통한 interpolation이 용이함을 보였다.
'CV' 카테고리의 다른 글
| [2025-1] 임수연 - Mask R-CNN (0) | 2025.02.22 |
|---|---|
| [2025-1] 전윤경- Multimodal Unsupervised Image-to-Image Translation (0) | 2025.02.21 |
| [2025-1] 주서영 - Flow matching for generative modeling (0) | 2025.02.20 |
| [25-1] 박지원 - Deep-Emotion: Facial Expression RecognitionUsing Attentional Convolutional Network (1) | 2025.02.19 |
| [2025-1] 주서영 - Adding Conditional Control to Text-to-Image Diffusion Models (0) | 2025.02.15 |




