https://www.youtube.com/watch?v=AHCt4Phgn9k&list=PL_iJu012NOxehE8fdF9me4TLfbdv3ZW8g&index=21
앞선 영상에서의 DQN, DDQN, Dueling DQN과 같은 방식들은 Value-based 방식으로, $\epsilon$-greedy를 통해 어떤 상태(s)에서 $\epsilon$의 확률로 랜덤하게 행동하고 그 중에서의 최선의 Q 값을 찾는 방식이다.
Policy-based
Policy-baesd 방식은 주어진 상황에서 어떤 선택을 선택할지에 대한 정책을 학습하여 추후 정책을 매개변수화된 확률 분포로 나타낸다. Policy-based가 Value-based 방식의 차이점은 다음과 같다.
- Value-based: ε의 확률로 랜덤하게 탐험을 진행하고, 1-ε의 확률로 현재 최적으로 판단되는 행동을 선택하여 결과적으로 Q-value를 최대화
- Policy-based: 학습된 정책을 기반으로 확률적으로 행동을 선택하는 방식이다.
Why Policy-based?
Policy-based를 사용하는 이유는 대표적으로 2가지가 있다.
- Continuous action 공간에서 잘 동작한다.
→ 정책이 연속적인 행동 공간에서도 직접적으로 확률분포를 생성할 수 있다. - Stochastic policy를 학습이 가능하다.
→ 확률적인 정책을 통해 동일 상태에서도 다양한 행동을 선택할 수 있다.
Stochastic policy
동일 상태에서도 다양한 행동을 선택할 수 있는지에 대한 예시를 아래 그림을 통해 확인해보자.

위 그림과 같은 상황에서 위쪽의 5칸의 상태(s)를 위,왼,오,아래의 벽의 유무로 나타내면 다음과 같이 나타낼 수 있다.
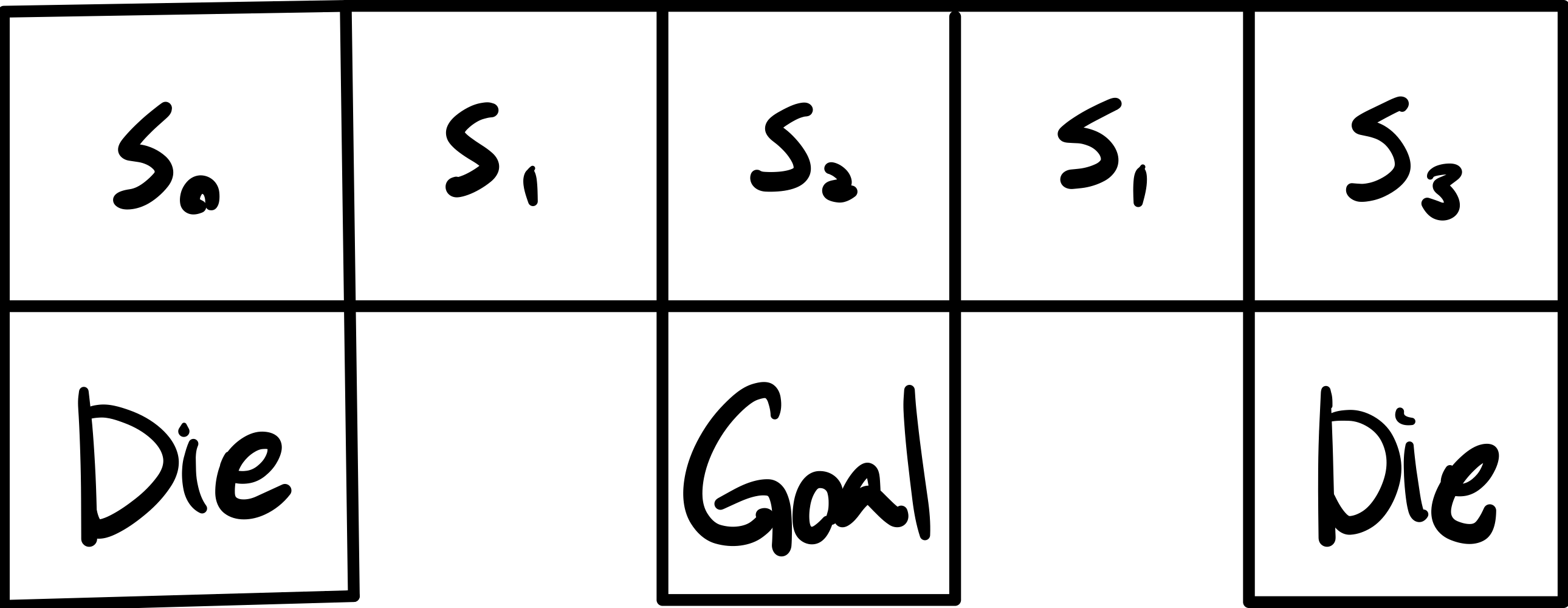
2번째 칸과 4번째 칸의 경우 둘 다 위,아래만 막혀있고 왼쪽, 오른쪽은 뚫려있어 $s={1,0,0,1}$로 동일한 상태가 되기 때문이다.
이때, 만약 학습을 통해 $Q(s_1,$왼$) > Q(s_1,$오$)$라고 한다면 초기 상태가 2번째 칸일 경우는 $s_0$과 $s_1$에서 계속 반복하게 되고, $Q(s_1,$왼$) < Q(s_1,$오$)$로 다시 학습을 하게 된다.
하지만 이 경우도 초기 상태가 4번째 칸일 경우 $s_1$과 $s_3$에서 계속 반복하게 된다.
이렇게 계속 학습을 진행하다보면 $P($왼$|s_1)=P($오$|s_1)={1\over2}$가 되어 각 상태에 도달했을 때 확률적으로 다른 행동을 하게된다.
결론
Policy-based 방식은 정책을 기반으로 행동을 선택하는 방식으로 Value-based와는 달리 연속적인 행동 공간과 확률적인 정책을 학습할 수 있다는 장점이 있다.
