[2025-2] 최민서 - SimPO: Simple Preference Optimizationwith a Reference-Free Reward

[논문링크] https://arxiv.org/abs/2405.14734

SimPO: Simple Preference Optimization with a Reference-Free Reward

 

DPO에 대해 잘 모른다면 논문을 이해하는데 힘들 수 있습니다.

 

[논문리뷰] https://blog.outta.ai/359

[2025-2] 최민서 - Direct Preference Optimization:Your Language Model is Secretly a Reward Model

 

1. Introduction

 

최근 LLM이 빠르게 발전하고 있고, LLM에 인간의 선호 경향성을 학습시키는 방법론(Reinforcement Learning from Human Feedback, RLHF)도 활발히 연구되고 있다. 기존의 RLHF 방식은 reward model을 학습시키고 policy model을 학습시키는 multi-stage 과정을 거치고 있어 그 과정이 효율적이지 못했다.

 

이후 Direct Preference Optimization(DPO)라는 offline 알고리즘이 등장하였다. DPO는 명시적인 reward model 없이도 재매개화를 통해 선호 데이터 쌍으로부터 policy model을 바로 학습시킬 수 있었다. DPO에서 implicit reward function은 현재 policy model과 supervised fine-tuned(SFT) model의 로그 비율로 표현되었는데, 이러한 reward 수식은 실제 LLM이 생성하는 답변의 우도와 일관되지 않는다. 본 논문에서는 이러한 차이가 성능 하락으로 이어짐을 보여준다.

 

이러한 문제를 해결하기 위해, Simple Preference Optimization(SimPO)를 제안한다. SimPO의 핵심은 reward function과 LLM의 generation metric이 일치하도록 만들어주는 것이다. SimPO는 아래의 두가지 핵심 구성요소를 가진다.

 

- Length-normalized reward를 구성하여, policy model이 생성하는 모든 토큰들의 로그 확률의 평균을 계산한다.

- 좋은 답변과 나쁜 답변의 차이를 확실히 하기 위해 target reward margin을 도입한다.

 

이러한 요소들을 바탕으로 SimPO는 아래와 같은 좋은 특성을 가진다.

 

- Simplicity

SimPO는 reference model을 필요로 하지 않기 때문에, 학습 과정이 DPO보다 효율적이다.

 

- Significant performance advantage

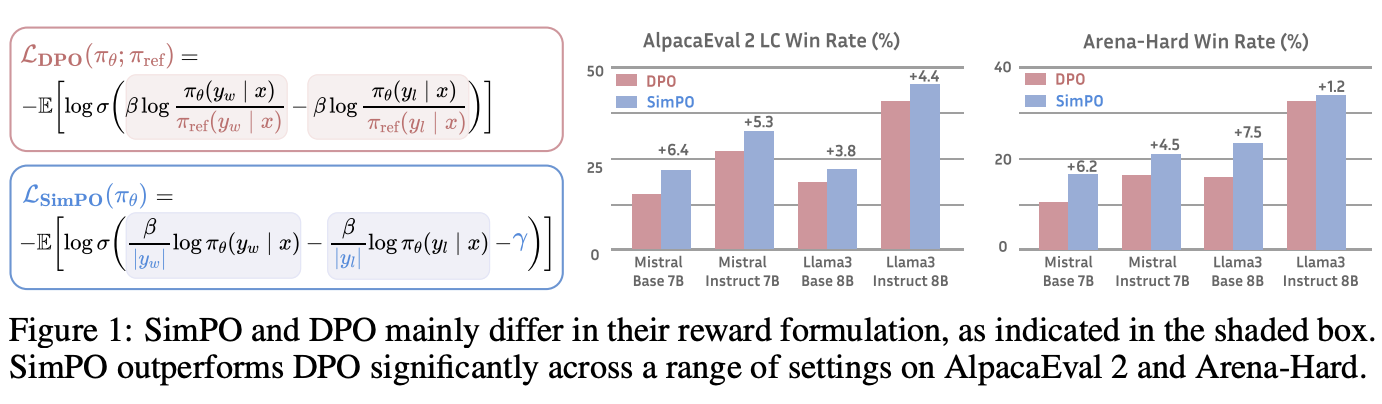
SimPO는 단순하지만, DPO보다 성능이 좋다. 이는 아래의 Table1에서 확인할 수 있다.

 

- Minimal length explitation

SimPO는 SFT나 DPO와 비교했을 때 긴 길이의 답변을 생성하지 않는다. 즉 단순히 길이가 긴 답변만으로 높은 reward를 받는 현상이 덜 발생한다.

 

 

2. SimPO: Simple Preference Optimization

 

2.1 Background: Direct Preference Optimization (DPO)

 

DPO는 명시적으로 reward model을 학습시키는 대신 reward function을 아래와 같이 policy model을 통해서 내재적으로 구성한다.

 

$$ r(x,y) = \beta \log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)} + \beta \log Z(x) $$

 

위 수식에서 $\pi_\theta$는 policy model, $\pi_{ref}$는 reference policy(SFT) model, $Z(x)$는 정규화 함수이다. Bradley-Terry(BT) 모델에 적용하여 아래와 같은 목적함수를 얻을 수 있었다. 

 

$$ L_{DPO}(\pi_\theta ; \pi_{ref}) = - \mathbb{E}_{(x,y_w,y_l)\sim \mathcal{D}} \left[ \log \sigma \left( \beta \log \frac{\pi_\theta(y_w|x)}{\pi_{ref}(y_w|x)} - \beta \log \frac{\pi_\theta(y_l | x)}{\pi_{ref}(y_l|x)} \right) \right] $$

 

2.2 A Simple Reference-Free Reward Aligned with Generation

 

Discrepancy between reward and generation for DPO

2.1의 DPO에서 한 것과 같이 reward model을 설정하면 아래와 같은 문제가 생긴다.

 

- DPO 파인튜닝을 위해 reference model $\pi_{ref}$가 필요하고 이를 별도의 (지도)학습을 통해 준비해 주어야 한다.

- 학습 중 최적화된 reward와 생성 과정에서 최적화된 로그 우도가 불일치하게 된다.

 

두번째 문제에 대해 더 자세하게 설명하면 인간 선호도를 반영한 triple data $(x,y_w,y_l)$이 있을 때, DPO에서는 $r(x,y_w) > r(x,y_l)$가 $p(y_w|x) > p(y_l|x)$를 의미하지는 않는다. 이는 DPO로 파인튜닝한 모델이 평균 로그우도의 관점에서 임의의 정확도 예측을 보여준다는 최근의 연구결과와도 일치한다.

위에서 언급한 $p(y|x)$는 policy model에 $x$라는 입력이 주어졌을 때 $y$라는 출력이 나올 (로그)우도이다. 따라서 각 토큰들의 로그우도의 합 혹은 평균 로그우도로 계산할 수 있다. DPO에서 reward의 계산에는 $\pi_{ref}$가 영향을 미치지만, $p(y|x)$의 계산에는 $\pi_{ref}$가 개입하지 않으므로 두번째 문제가 발생한다.

 

Length-normalized reward formulation

$r(x,y)$와 $p(y|x)$의 계산이 일관되지 않는다는 DPO의 문제는 reward function을 다른 방식으로 정의함으로써 해결할 수 있다. 하나의 방법은 reward를 토큰들의 로그우도의 합으로 정의하는 것이다. 이러한 정의는 policy model의 generation metric과 일치하지만, 모델이 length bias를 학습할 가능성이 높다. 따라서 이를 해결하기 위해 아래와 같은 평균 로그우도를 고려한다.

 

$$ p_\theta(y|x) = \frac{1}{|y|} \log \pi_\theta(y|x) = \frac{1}{|y|} \sum_{i=1}^{|y|} \log \pi_\theta (y_i | x, y_{<i}) $$

 

이는 $x$로부터 생성되는 답변 $y$의 로그우도를 답변의 길이 $|y|$로 나눈 것이다. 이를 reward function으로 아래와 같이 설정한다.

 

$$ r_{SimPO}(x,y) = \frac{\beta}{|y|} \log \pi_\theta(y|x) = \frac{\beta}{|y|} \sum_{i=1}^{|y|} \log \pi_\theta (y_i | x, y_{<i}) $$

 

$\beta$는 reward의 차이를 스케일링하여 조절하는 상수이다. 로그우도의 합을 전체 토큰 개수로 나누어주는 작업은 답변의 길이가 reward에 미치는 영향을 완화하여 policy model이 생성하는 답변의 품질을 높이는데 기여한다.

 

2.3 The SimPO Objective

 

Target reward margin

추가적으로, SimPO에서는 BT 목적함수에서 좋은 답변의 reward를 더 확실하게 높여주기 위해, target reward margin term $\gamma>0$을 아래와 같이 추가한다.

 

$$ p(y_w > y_l | x) = \sigma(r(x,y_w) - r(x,y_l) - \gamma ) $$

 

표준적인 학습환경에서 두 클래스의 margin term을 추가하는 것은 분류기의 일반화 성능을 높이는데 기여하는 것이 알려져 있다. Preference optimization 상황에서 두 클래스는 좋은 답변과 나쁜 답변을 의미한다. 실험적으로, 너무 크지 않은 margin term의 추가는 policy model의 성능 향상에 기여함을 확인할 수 있었다.

 

Objective

최종적으로 SimPO의 목적함수는 아래와 같이 나타난다.

 

$$ \mathcal{L}_{SimPO} (\pi_\theta) = - \mathbb{E}_{(x,y_w,y_l) \sim \mathcal{D}} \left[ \log \sigma \left( \frac{\beta}{|y_w|} \log \pi_\theta(y_w|x) - \frac{\beta}{|y_l|} \log \pi_\theta (y_l|x) - \gamma \right) \right]  $$

 

결과적으로, SimPO는 generation metric과 일관되는 reward function을 정립하여 목적함수의 학습이 실제 policy model의 성능 향상으로 이어질 수 있도록 하였고, 또한 margin term을 추가하여 학습에서의 효율성을 얻을 수 있었다.

논문의 Appendix F에서 DPO와 SimPO의 목적함수의 gradient를 비교분석하였다.

 

Preventing catastrophic forgetting without KL regularization

PPO나 DPO에서는 KL divergence 제약을 통해 RLHF로 파인튜닝한 모델이 기존의 reference model로부터 너무 크게 멀어지는 catastrophic forgetting 현상을 방지했다. SimPO에서는 명시적으로 제약을 주지는 않지만 실험적으로 아래와 같은 요인들을 조절해주면 reference model과의 낮은 KL divergence를 유지할 수 있었다.

 

- 작은 learning rate

- 다양한 도메인과 작업을 포괄하는 선호 데이터셋

- 이전의 지식을 까먹지 않고 새로운 데이터를 학습할 수 있는 LLM의 내재적 강건성

 

KL divergence와 관련된 실험은 Section 4.4에서 수행한다.

 

3. Experimental Setup

 

Models and training settings

논문에서는 두가지 모델을 두가지 세팅에서 파인튜닝한다. 

 

- 모델 : Llama-3-8B, Mistral-7B

- 세팅 : Base, Instruct

 

- Base setup

Zephyr의 학습 파이프라인을 따라간다. 먼저 base model(mistralai/Mistral-7B-v0.1, meta-llama/Meta-Llama-3-8B)을 UltraChat-200k dataset에서 학습시켜 SFT model을 준비한다. 이후 UltraFeedback dataset을 이용하여 preference optimization을 수행하여 SFT model을 파인튜닝한다. 이러한 세팅에서는 SFT model이 open-source data로 학습되기 때문에, high level of transparency를 가진다고 한다.

 

- Instruct setup

SFT model로 off-the-shelf instruction-tuned model(meta-llama/Meta-Llama-3-8B-Instruct, mistralai/Mistral-7B-Instruct-v0.2)을 사용한다. 이러한 모델은 광범위한 instruction-tuning 과정을 거친 모델이기 때문에 base setup에서 사용한 SFT model보다 강력하고 강건하다. 하지만 이러한 모델들은 RLHF 과정이 공개되어 있지 않기 때문에 SFT model과 preference optimization processs 사이에 distribution shift가 발생할 수 있다. 이를 완화하기 위해 SFT model을 이용하여 preference dataset을 생성한다. 이러한 방식은 on-policy setting과 유사하다. 구체적으로, UltraFeedback dataset에서 프롬프트 $x$를 얻고 SFT model을 이용해서 5개의 답변 $y$를 생성한다. 그리고 llm-blender/PairRM을 이용하여 5개의 생성된 답변의 점수를 계산하고 가장 높은 점수의 답변을 $y_w$, 낮은 점수의 답변을 $y_l$로 설정한다.

 

요약하자면, Llama-3-Base, Llama-3-Instruct, Mistral-Base, Mistral-Instruct의 4개의 setup에서 실험을 진행한다. DPO와 SimPO는 모두 하이퍼파라미터 튜닝을 진행했으며, SimPO의 경우 $\beta$ 값을 $2.0$에서 $2.5$ 사이로, $\gamma$ 값을 0.5에서 1.5 사이로 설정했다.

 

Evaluation benchmarks

학습된 policy model(LLM)의 성능은 MT-Bench, AlpacaEval 2, Arena-Hard v0.1의 세가지 벤치마크에서 측정되었다. 각 벤치마크의 특징은 아래와 같다.

 

Baselines

논문에서는 다른 offline preference optimization 방법들과 SimPO를 비교한다. 비교 대상 알고리즘들은 아래의 Table3에서 확인할 수 있다.

 

4. Experimental Results

 

4.1 Main Results and Ablations

 

주요 실험 결과는 아래와 같이 정리할 수 있다.

 

SimPO consistently and significantly outperforms existing preference optimization methods

아래의 Table4에서 확인할 수 있듯이 SimPO는 거의 모든 세팅에서 다른 방법들보다 우수한 성능을 보였다. 이는 SimPO의 학습 과정이 비교적 단순하다는 점에서 고무적인 결과이다. 

 

Benchmark quality varies

Table4에서 확인할 수 있듯이, MT-Bench는 reference optimization 방법론간 점수 차이가 크지 않았다. 이는 MT-Bench의 적은 데이터 개수와 단일 모델로 점수를 매기는 방식에 기인하는 것으로 추정된다. 반면 AlpacaEval 2와 Arena-Hard는 각 방법론간 충분한 점수 차이를 확인할 수 있었고, Arena-Hard가 AlpacaEval 2에 비하여 더 낮은 win rate를 보였다. 이를 통해 Arena-Hard가 더 어려운 벤치마크임을 암시한다.

 

The Instruct setting introduces significant performance gains

실험 전반에서 Instruct setup이 Base setup보다 좋은 성능을 보였다. 이는 SFT model이 파인튜닝의 시작점이라는 것과, SFT model이 좋은 품질의 preference data를 생성했고, 이를 다시 학습에 사용한 점에 기인한다.

 

Both key designs in SimPO are curcial

SimPO에 대해서 ablation study를 진행했다. Length Normalization(LN)을 제거한 것과 $\gamma$를 $0$으로 설정한 것 두 케이스의 결과를 아래 Table 5에서 확인할 수 있다. LN 없이 학습된 모델은 전반적으로 낮은 성능을 보였고 길고 반복되는 답변을 생성하는 경향이 있었다. $\gamma$를 $0$으로 설정했을 때 전반적으로 낮은 성능을 확인할 수 있었으며, 이를 통해 적절한 $\gamma$의 값이 $0$이 아님을 확인할 수 있다.

 

4.2 Length Normalization (LN) Prevents Length Exploitation

 

LN leads to an increase in the reward difference for all preference pairs, regardless of their length

BT 모델 하에서 목적함수는 reward의 차이 $\Delta r = r(x,y_w) - r(x,y_l)$가 target margin $\gamma$를 초과하도록 설정되었다. 논문에서는 학습된 모델에서 두 답변의 reward의 차이와 두 답변의 길이 차이 사이의 관계를 살펴보았다. 비교 대상 모델은 SFT 모델, SimPO 모델, length normalization을 사용하지 않은 SimPO 모델 이 세가지이다. 아래의 Figure 2a를 보면 SimPO의 경우 모든 답변 쌍에서 SFT 모델보다 높은 reward 차이를 관찰할 수 있었다. 반면 LN을 적용하지 않은 SimPO 모델의 경우 길이 차이가 음수인 경우에 reward의 차이가 음수가 나왔고, 이러한 경우에 학습이 제대로 되지 않음을 확인할 수 있었다.

 

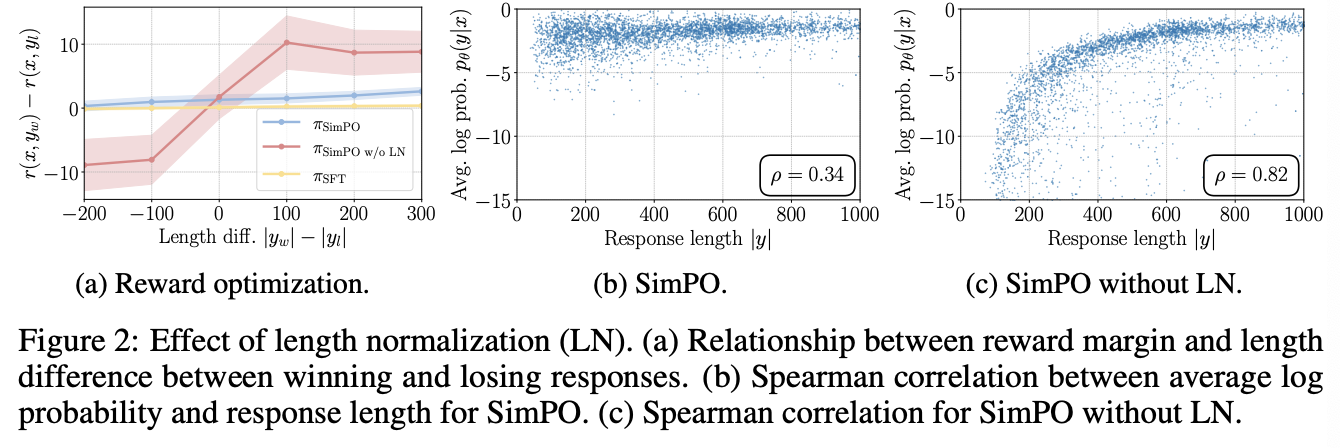
Removing LN results in a strong positive correlation between the reward and response length, leading to length exploitation

위의 Figure 2b와 2c에서는 SimPO와 SimPO without LN으로 생성한 prompt $x$에 대한 답변 $y$에 대해, 답변의 길이 $|y|$와 Average log probability $p_\theta(y|x) = \frac{1}{|y|} \log \pi_\theta (y|x)$의 축에 표시를 하였다. 결과적으로 SimPO without LN의 경우 SimPO 모델보다 훨씬 높은 Spearman correlation을 확인할 수 있었다. SimPO의 경우 SFT 모델과 유사한 Spearman correlation 계수를 보였다.

 

4.3 The Impact of Target Reward Margin in SimPO

 

Influence of $\gamma$ on reward accuracy and win rate

아래의 Figure 3a에서 reward margin $\gamma$의 크기에 따른 AlpacaEval2 benchmark에서의 win rate와 reward accuracy의 관계를 확인할 수 있다. $\gamma$의 값이 커짐에 따라 reward accuracy가 증가하고, win rate는 증가하다가 감소한다. 즉 일반적으로 $\gamma$의 값이 커질수록 reward의 정확도가 높아지지만, reward margin $\gamma$ 값만이 정확도에 영향을 미치는 것은 아니다.

 

Impact of $\gamma$ on the reward distribution

위의 Figure 3b, 3c에서 확인할 수 있듯이, reward margin $\gamma$의 값이 커질수록 reward difference와 더 좋은 답변 $y_w$의 평균 로그 확률분포는 평탄화되며 좋은 답변의 로그 우도가 낮아지게 된다. 이것은 초기에는 모델의 성능을 향상시킬 수 있지만 결과적으로 모델의 생성 성능 하락으로 이어질 수 있다. 논문에서는 $\gamma$의 값을 설정하는 과정에서 true reward distribution을 정확하게 예측하는 것과 잘 보정된 우도를 유지하는 것 사이의 trade-off 관계가 있다고 가설을 설정하고 이를 후속 연구에서 다룰 것을 언급한다.

 

4.4 In-Depth Analysis of DPO vs. SimPO

 

해당 섹션에서는 SimPO와 DPO를 아래의 네 가지 관점에서 비교한다. 결과적으로 SimPO가 DPO보다 성능이 좋음을 보인다.

 

(1) likelihood-length correlation

(2) reward formulation

(3) reward accuracy

(4) algorithm efficiency

 

DPO reward implicitly facilitates length normaliation

DPO의 reward 수식 $r(x,y) = \beta \log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)}$에는 length normalization term이 없지만, reference model과 policy model의 로그 비율을 따지는 것이 내재적으로 length bias를 예방하는 효과가 있다. 이는 아래의 Figure 4a와 Table 6에서 확인할 수 있고, SimPO보다는 덜하지만, SimPO without LN보다는 length bias 효과가 적게 나타남을 확인할 수 있다.

 

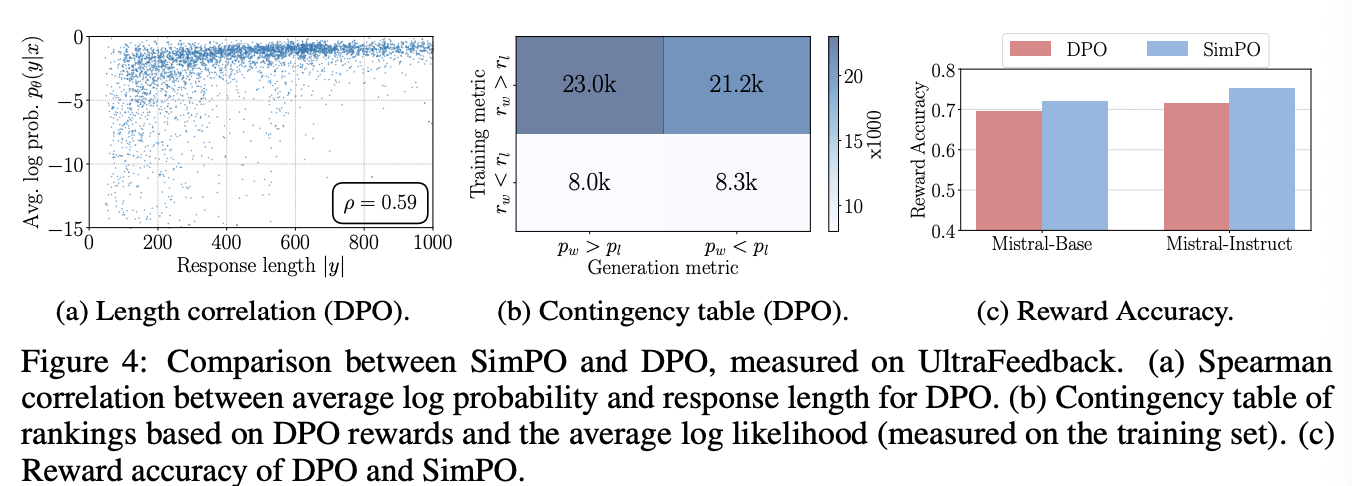
DPO reward mismatches generation likelihood

앞서 설명했듯이, DPO의 reward 수식 $r_\theta(x,y) = \beta \log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)}$와 평균 로그 우도 generation metric $p_\theta(y|x) = \frac{1}{|y|} \log \pi_\theta(y|x)$는 다르기 때문에, DPO로 학습된 모델에서 높은 로그 우도를 가진 답변이 일반적으로 reward 값이 높다고 하기 힘들다. 위의 Figure 4b에서 확인할 수 있듯이, UltraFeedback training set의 사례에서 $r_\theta(x,y_w) > r_\theta(x,y_l)$인 경우 중 절반 이상의 데이터가 $p_\theta(y_w|x) < p_\theta(y_l|x)$임을 확인할 수 있었다.

 

DPO lags behind SimPO in terms of reward accuracy

위의 Figure 4c에서 SimPO와 DPO의 reward accuracy를 비교했고 SimPO가 DPO보다 더 높은 점수를 얻음을 확인할 수 있었다. 여기서 말하는 reward accuracy란 학습된 모델의 reward 모델이 실제 preference dataset과 얼마나 부합하는지를 측정한 점수이다.

 

KL divergence of SimPO and DPO

아래의 Figure 5a에서 DPO와 SimPO의 KL divergence를 비교하였다. KL divergence는 $y_w$에 대한 KL divergence로 학습 중 held-out set으로 측정하였다. 그림에서 볼 수 있듯이 SimPO는 reference model과의 KL regularization term이 없지만, 비교적 낮은 KL divergence를 유지함을 확인할 수 있었다. 또한 Figure 5b에서 볼 수 있듯이, 해당 세팅에서 SimPO가 DPO보다 LC 지표가 더 높았고 하이퍼파라미터 $\beta$의 크기가 작을수록 LC 점수가 높았다. 이를 통해, reference model이 약할 때, policy model이 reference model로부터 멀리 떨어지지 않도록 엄격하게 규제하는 것이 좋지 않다고 가설을 설정할 수 있다. 주의할 점은, 논문에서 파인튜닝 중 학습 붕괴나 생성 퇴화 등의 현상이 일어나지는 않았지만 SimPO는 명시적인 KL 규제가 없는만큼, reward hacking이 일어날 수도 있다.

SimPO is more memory and compute-efficient than DPO

위의 Figure 5c에서 확인할 수 있듯이 SimPO는 DPO와 비교했을 때 컴퓨팅자원을 덜 소모한다.

 

5. Conclusion

 

SimPO는 간단하지만 효과적인 preference optimization 알고리즘이다. reward 함수를 generation likelihood와 일치시키고, target reward margin을 추가함으로써 SimPO는 reference model의 명시적 표현을 제거한 목적함수를 얻을 수 있었고, length bias 문제 또한 해결할 수 있었다.