[2024-2] 이재호 RNN, LSTM, GRU

RNN, LSTM, GRU는 모두 순환신경망(Recurrent neural networks)의 변형으로 순차적인 데이터(sequence data)를 처리하기 위해 설계된 알고리즘입니다. 각각의 알고리즘의 아키텍처와 특징에 대해 알아보겠습니다.

 

# Fundamentals of Recurrent Neural Network(RNN) and Long Short-Term Memory (LSTM) Network - Alex Sherstinsky (2018)

https://arxiv.org/abs/1808.03314

Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network

 

# Architecture

RNN 기본 구조

먼저 용어 정리를 하고 가겠습니다.

 

• 시퀀스 : 단어가 나열된 문장과 같이 특정 순서에 의해 나열된 데이터를 의미합니다.
• 셀 : RNN의 은닉층에서 활성화 함수를 통해 결과를 내보내는 역할을 하는 노드를 의미합니다.
• 은닉 상태 : 셀에서 출력되는 값으로 h_t로 표기합니다.

한 방향으로만 진행되었던 feed forward neural network와 다르게 RNN은 loop을 통해 신호가 두 방향으로 전달됩니다. 이러한 순환 구조를 통해 RNN은 자연어 처리, 음성 인식, 시계열 데이터 등에 사용됩니다.

 

위 그림에서 현재 시점의 hidden state $ h_t $ 는 전 단계의 hidden state  $ h_{t-1} $ 와 현재 시 $ x_t $ 로 구성됩니다. $ h_{t-1} $ 는 이전 상태의 정보를 반영된 값이므로 현재의 hidden state는 과거의 정보와 현재의 정보를 다 가지고 있는 값이라고 볼 수 있습니다. $ h_t $ 를 계산할 때 사용하는 weight와 bias 값들은 모든 셀에서 동일하고 activation function tanh 또한 모든 셀에서 동일하게 사용합니다. 그리고 현재의 타임 스텝에서 결과 값 $ y_t $ 를 출력하고 싶으면 다른 weight와 bias를 추가해서 출력할 수 있습니다. 아래 그림에서 알 수 있듯이 구조에 따라 결과 값을 출력하는 방식이 다릅니다.

 

다양한 RNN의 구조

Input 값과 output 값의 개수에 따라 다양한 RNN의 구조가 존재합니다. 또한 VGGNet이나 ResNet에서 레이어를 깊게 했을 때 성능이 높아졌듯이 RNN도 레이어를 깊게 할 수 있습니다.

 

# 문제점

RNN의 gradient flow

RNN의 구조에는 gradient exploding과 gradient vanishing과 같은 문제가 있습니다.

우선  $ \frac{\partial L}{\partial h_{t-1}} $ 를 구해보면 Chain rule에 의하여 $ \frac {\partial L}{\partial h_t} $ · $ \frac {\partial h_t}{\partial h_t-1} $ 이 됩니다. 이때 $ h_t = tanh(W(h_{t-1} + x_t) +b) $ 식을 통해 $ \frac {\partial h_t}{\partial h_{t-1}} $ 를 계산해 보면 $ (1-tanh^2) × W $ 가 됩니다. 그리고 모든 셀에서 같은 $ W $ 값을 사용하게 되므로 앞쪽 layer로 올수록 upstream gradient에 같은 $ W $를 거듭제곱한 값이 gradient에 포함되게 됩니다. 따라서 $ W $의 원소 값이 1보다 크면 그 원소들은 매우 커지는 gradient exploding 문제가 1보다 작으면 그 원소들은 매우 작아지는 gradient vanishing 문제가 발생하게 됩니다. 따라서 RNN은 긴 시퀀스의 데이터를 학습하는데 한계가 존재합니다.

 

# Long Short Term Memory (1997) - Hochreiter and Schmidhuber

https://www.bioinf.jku.at/publications/older/2604.pdf

기존 RNN 구조의 한계점인 gradient vanishing, gradient exploding은 LSTM이라는 알고리즘으로 해결이 됩니다. 

 

# Architecture

왼쪽은 LSTM에서 하나의 cell 구조를 오른쪽은 $ c_t $와 $ h_t $가 연산되는 과정을 보여준다.

• $ c_t $ : cell state로 LSTM에서 Long term memory를 의미한다.
• $ h_t $ : hidden state로 LSTM에서 Short term memory를 의미한다.
• $ x_t $ : 현재 시점의 input을 의미한다.
• $ i $ : input gate으로 $ g $의 값을 얼마나 반영할지 정합니다.
• $ f $ : forget gate으로 $ c_t $(현재 시의 장기기억) 값을 계산할 때 $ c_t-1 $(직전 상태의 장기기억)을 얼마나 반영할지 정합니다.
• $ o $ : output gate으로 $ h_t $(현재상태의 단기기억)을 계산할 때 $ c_t $ 값을 얼마나 반영할지 정합니다.
• $ g $ : 장기 기억에 포함될 새로운 정보를 의미합니다. (편의상 g도 하나의 gate로 설명하겠습니다)

RNN과 비교해 $ c_t $와 $ i, f, o, g $ 4개의 gate가 생겼습니다. 우선 $ i, f, o, g $가 어떻게 만들어지는지 알아보겠습니다.

 

$ i, f, o, g $ 가 만들어지는 과정

$ x_t $ 와 $ h_{t-1} $의 h-dimensional vector을 수직으로 쌓으면 2h-dimensional vector가 됩니다. 이를 크기가 4h x 2h인 weight matrix와 곱해주면 4h-dimensional vector가 됩니다. 이를 4개의 h-dimensional vector로 나누어 activation function을 통과시켜주면 4개의 gate가 완성됩니다. 이때 $ i, f, o $ 는 sigmoid를 $ g $는 tanh를 activation function으로 사용했음을 알 수 있습니다. 따라서 $ i, f, o $는 0 ~ 1의 값을 가지게 되고 $ g $는 -1 ~ 1 사이의 값을 가진다는 것을 기억해 둡시다. 참고로 위 그림에서는 $ W $를 하나의 4h x 2h matrix로 보았지만 다른 설명에서는 각 gate에 해당하는 4개의 weight $ W_i $, $ W_f $, $ W_o $, $ W_g $로 나누어 설명하기도 합니다.

 

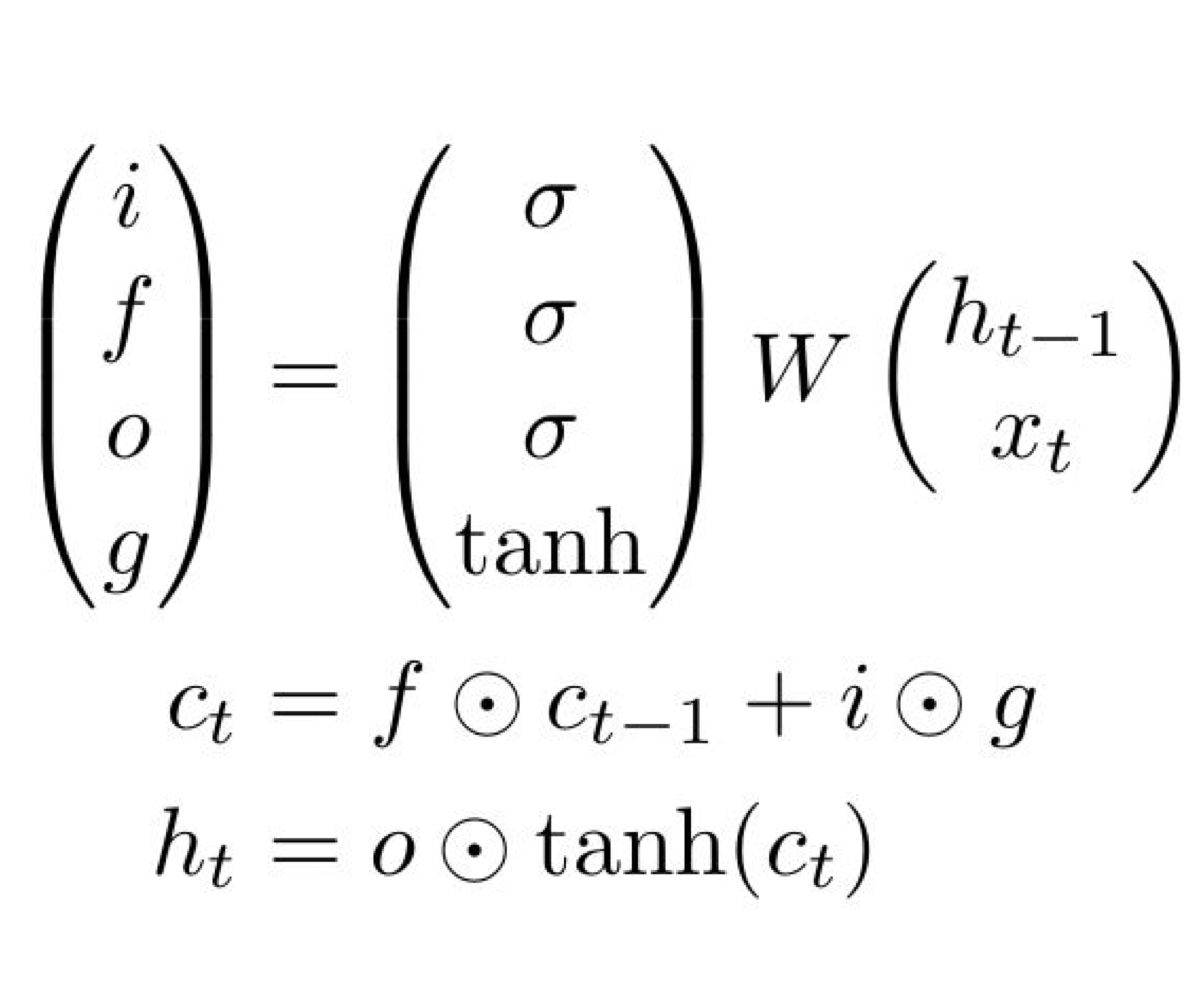
이제 위 그림에서  $ c_t $, $ h_t $가 무엇을 의미하는지 $ i, f, o ,g $ gate가 어떻게 만들어지고 값의 범위가 어떻게 만들어지는지 알았습니다. 그러면 위의 수식의 의미에 대해 알아봅시다. $ c_t $는 현재 시점에서의 장기기억을 의미합니다. 그리고 여기서 $ f $와 $ c_{t-1} $의 element wise multiplication을 진행해 줍니다. 이를 통해 $ c_{t-1} $중 얼마나 $ c_t $로 가져갈지를 정해줍니다. 모두 가져간다면 $ f $ 의 값이 1 모두 안 가져간다면 $ f $의 값이 0이 될 것입니다. 이후 $ i $와 $ g $에 대해서도 element wise multiplication을 진행해 줍니다. 이때 $ g $는 새롭게 기억될 정보를 의미하는 -1 ~ 1 사이의 숫자들이고 $ i $는 앞에서와 마찬가지로 이러한 $ g $ 값들을 얼마나 $ c_t $에 반영할지 정해줍니다. 이렇게 해서 현재 시에서의 장기 기억을 나타내는 값이 $ c_t $가 완성됩니다. 이제 완성된 $ c_t $를 tanh 함수를 통과 시켜준 뒤 $ o $와 element wise multiplication을 해줍니다. $ o $는 장기 기억 중 얼마나 단기 기억으로 가져갈지를 정해줍니다. 참고로 Element wise multiplication이 진행되었으므로 $ c_t, h_t, i, f, o, g $ 는 모두 h-dimensional vector입니다.

 

# Gradient 문제를 해결한 방법

 

이제 LSTM이 어떻게 구성되고 작동되는지 알았습니다. 그러면 이러한 구조가 RNN에서의 gradient exploding과 gradient vanishing 문제를 어떻게 해결할 수 있었는지 알아보겠습니다.

LSTM에서 $ c_t $에 대한 gradient flow

 

$ c_t $를 따로 정의함으로서 각 cell로 들어오는 upstream gradient를 계산하기 용이해졌습니다.

$ \frac{\partial L}{\partial c_{t-1}} $ 값을 계산해 보면 Chain rule에 의하여 $ \frac {\partial L}{\partial c_t} $ · $ \frac {\partial c_t}{\partial c_{t-1}} $이 되고 이때 $ \frac {\partial c_t}{\partial c_{t-1}} $는 $ c_t $의 식에 의해 $ f $가 됩니다. 따라서 $ c_t-1 $의 gradient는 upstream gradient인 $ \frac {\partial L}{\partial c_t} $에 현재 시에서의 $ f $를 곱해주면 됩니다.

$ \frac{\partial L}{\partial c_{t-1}} $ = $ \frac {\partial L}{\partial c_t} $ · $ f $

RNN에서 gradient 문제가 발생했던 이유는 같은 값을 계속해서 곱해주어야 하기 때문이었습니다. 하지만 $ f $는 $ h_{t-1} $, $ x_t $, $ W $로 이루어지고 $ h_{t-1} $, $ x_t $는 cell 마다 값이 다르기 때문에 $ f $의 값도 바뀌게 됩니다. 따라서 gradient 문제를 해결할 수 있습니다. 이는 ResNet에서 identity layer와 비슷한 효과로 보실 수 있습니다.

 

# Gated Recurrent Neural Network - Junyoung Chung, Caglar Gulcehre, KyungHyun Cho (2014)

https://arxiv.org/abs/1412.3555#

Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling

GRU는 기존 LSTM의 구조를 더 간단하게 개선한 모델입니다. 한국인 조강현 박사님이 제안하신 방법입니다. 

 

# Architecture

GRU의 구조

LSTM에서는 input gate, forget gate, output gate 을 사용했지만 GRU에서는 reset gate, update gate 2개의 gate만을 사용합니다. 또한 cell state, hidden state가 합쳐져 하나의 hidden state로 표현하고 있습니다.

 

Reset gate는 (2)번 식을 이용해 구해집니다. 이전 시점의 hidden state와 현시점의 x를 sigmoid 활성화 함수에 적용하여 구하는 방식입니다. 이는 0 ~ 1 사이의 결과 값을 가지게 되며 전 단계의 hidden state의 정보를 얼마나 활용할지 정해줍니다. reset gate의 값은 그대로 사용되지 않고 (3) 번 식과 같이 활용됩니다. 여기서 $ \tilde {h}^{t} $ 는 현시점의 정보 후보군을 의미합니다. 

 

Update gate는 (1)번 식을 이용해 구해집니다. LSTM의 $ i, g $ 와 비슷한 역할을 하며 과거와 현재 정보를 얼마나 반영할지에 대한 비율을 구해줍니다. (1)번 식을 통해 구한 $ z_t $는 현재 정보를 얼마나 반영할지 $ (1-z_t) $는 과거 정보를 얼마나 반영할지 정해줍니다. 최종적으로 현재 시점의 hidden state $ h_t $를 (4)번 식을 통해 구할 수 있습니다.

 

GRU는 기존 LSTM에 비해 더 간단한 구조를 가지고 있으며 마지막 출력 값에 활성화 함수를 적용하지 않습니다. LSTM과 비교 결과 주제별로 LSTM이 좋기도 GRU가 좋기도 하다는 결과가 나왔습니다. 하지만 GRU가 LSTM에 비해 학습할 가중치가 적다는 이점이 있습니다.