[2025-2] 박제우 - Sharpness-Aware Minimization for Efficiently Improving Generalization

https://arxiv.org/abs/2010.01412

Sharpness-Aware Minimization for Efficiently Improving Generalization

 

Abstract

현대 딥러닝 모델은 대부분 Overparameterized된 경우가 많다. 이러한 상황에서는 Train Loss의 감소만으로 최적을 보장할 수 없다. 

 

따라서 손실 지형(Loss Landscape)의 평평함과 모델의 일반화 성능은 높은 관련이 있기 때문에, min-max 최적화를 통해 Flat Minima를 찾아가는 방법론이라고 요약할 수 있겠다. 

 

하지만 본 연구는 2021년에 발표되었고 이를 보완한 후속 연구도 많으나, 경험적으로 이 이후에도 Adam계열 Optimizer가 더 널리 쓰이기는 한다.

 

1. Introduction

Overparameterized된 현대 딥러닝 모델의 Training Loss Landscape는 복잡하고 Non-Convex하기 때문에 다수의 Local Minima를 포함한다. 

 

이러한 Local Minima는 당연히 일반화 성능 저하를 야기한다고 선행연구에 의해서 많이 입증되었다.

 

그러나 명시적으로 Flat Minima를 탐색하면서 더 나은 일반화 성능을 향해 가는 알고리즘은 아직까지 완벽히 제시되지는 않았다. 

 

따라서 본 연구에서는 손실 지형의 기하학과 일반화 성능 사이의 관계를 활용한 Optimization 방식을 제안한다. 

 

Contribution

1) Sharpness Aware Minimization(SAM) 방식은 Loss 와 Loss Landscape의 Sharpness를 동시에 최적화해서 모델의 일반화 성능을 향상시킨다. 이는 특정 지점에서의 손실이 낮은 방향으로 최적화하는 것이 아닌, 인접 지역의 손실을 동시에 최소화한다. 

 

2) 이를 통해 CIFAR, IMAGENET 등 다양한 CV Task에서 SOTA를 달성했다. 

 

3) SAM은 노이즈에 대해서도 강건성을 보였다.

 

2. Sharpness Aware Minimization

기본적인 SGD나 Adam과 같은 최적화 방식에서는 파라미터 w에 대해 손실을 최소화하는 접근법을 일반적으로 상정한다.

그러나 일반적으로 현대에는 손실 L은 w에 대해 non-convex하기 때문에 단순히 L을 최소화하는 것 만으로는 Optimal Status를 보장하지 못한다. 

 

따라서 본 연구는 손실값 Ls를 낮게 하는 파라미터 w를 찾는게 아닌 해당  파라미터 w 근처의 이웃(neighboring) 파라미터에서 손실값이 균일하게 낮은 지역을 탐색한다.

 

Theorem 1

임의의 \rho에 대해 분포 D로부터 생성된 훈련 집합 S에 대해 높은 확률로 다음이 성립한다. 여기서 h는 정규화항이다.

 

여기서 파라미터 w 주변 반지름 \rho 안쪽의 구역에서의 Sharpness를 정량화하기 위해 다음과 같이 정의한다. 

 

h에 관한 상세한 내용은 Appendix A의 증명에서 나오므로, 이하부터는 보기 쉽게 L2 정규화 항을 사용한다.

min-max 최적화 수식은 다음과 같이 쓸 수 있다.

이는 Lsam을 파라미터 w 주변의 \epsilon 안에서 가장 손실이 큰 지점이라고 정의하고, 이 Lsam을 최소화시키는 min-max 최적화를 나타난 것이다.

여기서 \rho는 하이퍼파라미터인데, 그냥 관성적으로? 0.05를 많이 쓰는 것 같다. 다만 비교적 소규모 모델에서는 0.15를 최적으로 쓴 선행 연구도 있었다.

 

Lsam을 구하는, 즉 maximize 문제는 1차 테일러 전개를 통해서 근사한다. 즉 다음과 같이 전개할 수 있다. 

 

이는 직관적으로 손실을 가장 악화시키는 파라미터 교란 \epsilon을 찾는다고 볼 수 있다.

 

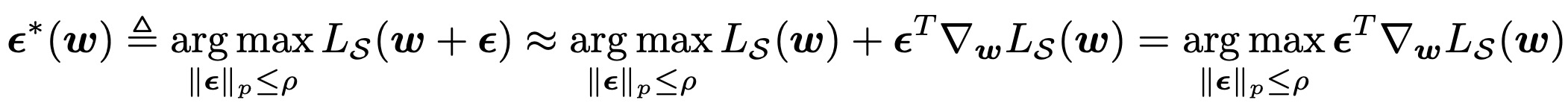
해를 구하는 과정을 생략하고, 바로 넘어가자면 \epsilon은 다음과 같이 정의된다.

 

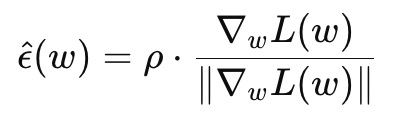
당연히 근사한 값이기 때문에 완벽히 그렇다고는 볼 수 없으나 거의 그 경계선에서 가장 손실이 크게 증가한다.

즉 \rho는 결국 '얼마나 넓은 범위가 평평해야 최적이라고 보는가' 를 나타낸다

 

이렇게 Inner Maximization을 수행한 뒤에 Outer Minimization은 일반적인 SGD, Adam 등을 사용해도 무방하다. 

 

알고리즘을 간단히 요약하면 다음과 같다.

 

1. 현재 weight에서 gradient 계산

2. 그 gradient 방향으로 \rho만큼 이동 (최악의 perturbation)

3. 이동한 위치에서 gradient 재계산

4. gradient로 원래 weight 업데이트

 

그림으로 보면 더 잘 이해가 될 것 같다. 

위 그림의 W_{t+1}이 일반적인 SGD로 업데이트 했을 때의 최적화 지점이고, 

 

Wadv가 가장 손실을 급격하게 만드는 지점이다. 

 

Wadv 지점에서 새로 계산된 그래디언트가 파란색 화살표이고, 그 방향대로 Wt를 업데이트 하면 더 평평한 지점인 Wsam_{t+1}에 도달하게 된다. 

 

논문의 Appendix에 본 내용에 대한 더욱 엄밀한 증명과 전개가 나와있다.