[2025-2] 김지원 - Introduction to Reinforcement Learning

Miscellaneous

[2025-2] 김지원 - Introduction to Reinforcement Learning

jw103203 2025. 9. 13. 00:14

논문 정보: Ghasemi, M., & Ebrahimi, D. (2024). Introduction to reinforcement learning. arXiv preprint arXiv:2408.07712.

논문 링크: https://arxiv.org/pdf/2408.07712?

논문 인용수: 17회 (2025.09.12 기준)

Introduction

강화 학습은 AI의 한 분야로 시간에 따른 누적 보상을 최대화하는 것을 목표로 환경과 상호작용함으로써 훈련된다.

지도 학습&비지도 학습과 달리 RL은 직관적인 결정들을 내려야 하는 자율적인 에이전트들을 다루고 종종 데이터 없이 이들의 행동으로부터 학습하기도 한다.

핵심 아이디어는 시행착오 탐색을 통해 시간을 지나 누적 보상을 최대화하기 위해 어떻게 세상이 작동하는 지를 배우는 것이다(=어떤 행동이 긍정적 보상을 주는지).

RL에는 여러 핵심 개념이 있다: 상태, 행동, 정책, 보상, 전이 역학(확률), 환경 모델.

상태 $s\in S$ 는 특정 시점에 에이전트가 인식하는 환경의 특정 조건 또는 구성

상태는 discrete할 수도 continuous할 수도 있다.

행동 $a \in A$는 에이전트가 환경과 상호작용하여 만들 수 있는 가능한 움직임 또는 결정들의 집합

선택된 행동은 현재 상태와 정책에 따라 요구되는 목표들에 도달하기 위해 에이전트가 시행하는 전략의 일부이며 행동도 discrete할 수도 continuous할 수도 있다.

정책 $\pi$는 인식한 환경의 상태를 행동으로 매핑함으로써 에이전트의 행동을 안내한다.

정책들은 stochastic(확률적)일 수 있으며 특정 행동을 취할 확률을 정의한다.

확률론적 정책 $\pi(a|s)$는 주어진 상태에서 가능한 행동들의 확률 분포를 의미한다.

단일 행동을 선택하는 것 대신 정책에 의해 정의된 확률을 기반으로 행동을 샘플한다.

반면 결정론적 정책 $\pi(s)=a$는 특정 행동으로 직접적으로 매핑한다.

보상 $r \in R$은 시간에 걸쳐 달성할 국소 목표와 전역 목표들을 정의하면서 각 시간에 에이전트에게 목표를 제공해주기 때문에 중요한 요소이다.

이는 결정론적일 수도 $\mathcal{R}(s,r)=r$ 또는 확률론적일 수도 $P(r|s,a)$ 있다.

전이 역학(확률) 함수는 현재 상태 s와 행동 a가 주어질 때 새로운 상태 $s'$에 도달할 확률을 정의

즉, $\mathcal{P}(s'|s,a)$로 작성된다.

환경 모델은 상태와 행동으로부터 주어진 특정 입력에 대해 어떤 것이 가능한지(다음 상태와 보상) 매핑하는 환경의 근사 또는 예측이다.

가능한 미래 이벤트들을 근거로 어떤 행동이 취해져야 하는 지 식별함으로써 이러한 모델이 계획하는 것을 돕는다.

모델 기반 접근법이 있는 반면 오로지 시행 착오 학습에 의존하는 model-free 접근법이 존재한다.

→위 내용은 섹션 3에서 더 다룬다.

환경의 역학은 전이 함수와 보상 함수로 표현된다.

이들을 함께 엮어서 Markov Decision Process(MDP)로 표현한다.

$\mathcal{M}=(\mathcal{S}, \mathcal{A}, \mathcal{P},\mathcal{R}, \gamma)$

이때 각각 상태, 행동, 전이 역학, 보상함수이며 $\gamma$는 할인율이다. $\gamma\in[0,1]$

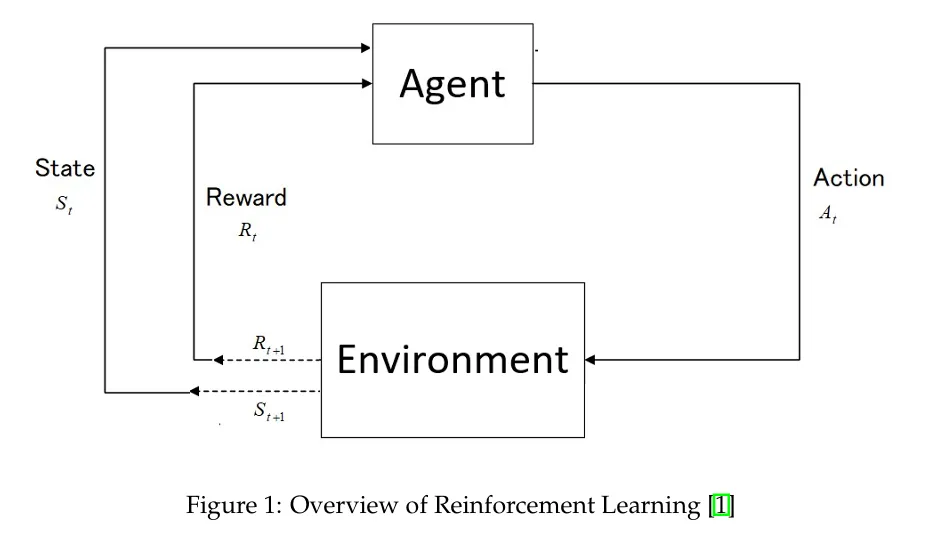
Backgrounds & Key Concepts

2.1 Multi-Armed Bandit(s)

Multi-Armed Bandit는 에이전트가 시간에 따라 누적되는 보상들을 최대화하기 위해 반복적으로 $\mathcal{K}$ 행동들(또는 arms)로부터 에이전트가 선택하는 단순화된 의사 결정 시나리오를 나타낸다.

각 행동은 exploration과 exploitation의 균형을 맞추는 미지의 보상 분포와 관련있다.

Exploration: 모든 행동들에 대한 정보 수집하기 위한 탐색 과정

Exploitation: 가장 잘 아는 행동을 사용하여 즉각적인 보상을 최대화하도록 실행하는 과정

$\mathcal{K}$-armed bandit 문제에서 각 행동 $a \in \{a_1,a_2,...,a_k\}$는 정적인(시간불변인) 확률 분포로부터 보상을 산출한다.

각 가능한 $k\in \mathcal{K}$ 행동들에 대해 예상 평균 보상이 존재하며 → 이는 행동의 가치로 표현된다.

$A_t$가 t 스텝에서 선택된 행동일 때 $R_t$는 상응하는 보상이고 행동의 참 값은 $q_*(a)$ 행동에 대한 예상 보상으로 정의된다.

$q_*(a)=\mathbb{E}[\mathcal{R}_t|\mathcal{A}_t=a]$

만약 $q_(a)$가 모든 a에 대해 알려져 있다면 문제는 자명하다(trivial): 에이전트는 가장 높은 $q_(a)$를 가지는 행동을 선택해야 한다.

하지만 실제로는 모르고 추정해야 하는데 추정 끝에 가장 높은 값을 가지는 행동을 **“greedy action”**이라고 한다.

이때 greedy action을 선택하는 것은 즉각적인 보상을 위한 현재 지식을 이용(Exploitation)하는 것인 반면 non-greedy action을 선택하는 것은 추정치를 향상하기 위해 탐색(Exploartion)하는 것이다.

Exploration과 Exploitation 간의 균형을 맞추는 것은 RL에서 매우 중요하다.

Exploitation을 선택하는 것은 즉각적인 보상을 최대화하지만 Exploration은 다양한 요소들에 따라 전반적인 높은 보상을 가져다 줄 수 있기 때문이다.

샘플링 평균을 통해 행동 value들을 추정하는 것은 stationary bandit 문제에서는 효과적이지만 실세계 non-stationary 환경에서는 최근 보상에 큰 가중치를 두는 것이 현명하다.

행동 value 업데이트에 다음의 업데이트 룰이 적용된다(sample-average method):

$\mathcal{Q}t(a)=\frac{\Sigma{i=1}^{t-1}\mathcal{R}i\cdot1{\mathcal{A}i=a}}{\Sigma{i=1}^{t-1}1_{\mathcal{A}_i=a}}$

여기서 $1_{\mathcal{A}_i=a}$는 indicator 함수로 행동 a가 step i에 선택되면 1 그렇지 않으면 0을 나타낸다.

시간에 따라 대수의 법칙에 의해 $\mathcal{Q}t(a)$는 $q*(a)$로 수렴한다.

위 수식은 다른 방법으로 작성될 수 있는데 바로 행동 value $\mathcal{Q}_t(a)$를 시점 t까지의 행동에서 받은 보상들의 평균으로 작성 가능하다

반복적으로 $\mathcal{Q}_t(a)$를 재정의하기 위해 아래와 같은 증분적 업데이트 규칙을 사용:

$\mathcal{Q}_{n+1}=\mathcal{Q}_n+\alpha|\mathcal{R}_n-\mathcal{Q}_n|$

여기서 $\alpha$는 학습률(= step-size 파라미터; 얼마나 새 정보가 옛 추정치를 override할지 결정)

다시 말해, “NewEstimate ←OldEstimate + StepSize[Target - OldEstimate]”

multi-armed bandit 문제를 풀기에 가장 어려운 문제는 Exploration과 Exploitation의 균형을 맞추는 것이다.

$\epsilon$-greedy 방법

확률 $\epsilon$로 랜덤 액션을 선택(exploration) 그렇지 않으면 ($1-\epsilon$의 확률로) greedy action을 선택한다(exploitation).

비록 suboptimal한 행동(Exploration)을 덜 자주 고르긴 하지만, 이는 모든 행동들이 샘플링되도록 한다.

Upper Confidence Bound(UCB)

이는 행동 선택에 불확실성을 통합함으로써 Exploitation과 Exploration의 균형을 맞춤

$A_t=\arg\max_a[\mathcal{Q}_t(a)+c\sqrt{\frac{\ln t}{\mathcal{N}_t(a)}}]$

이때 $\mathcal{N}_t(a)$는 t시점까지 a가 선택된 횟수이며 $c>0$이 Exploration 비율을 통제함

UCB는 높은 불확실성과 적은 샘플링 횟수를 가진 행동을 우선 시 한다.

Optimistic Initialization은 조기에 모든 행동의 탐색을 독려하기 위해 $\mathcal{Q}_1(a)$에 높은 초기 값을 할당한다.

예를 들어, $\mathcal{Q}_1(a)=+5$ 세팅은 시도하지 않은 행동들이 더 초기에 매력적이도록 만든다.

하지만 이들은 이론적으로는 장기적으로 benefit이지만 실용적인 효과성을 직접적으로 나타내진 않음

행동 값의 초기 추정 (=$\mathcal{Q}_1(a)$)는 학습 과정에 중요한 역할을 한다.

초기 추측은 에이전트의 초기 결정에 영향을 줌

sample-average 방법이 각 행동이 한번 선택된 이후에 초기 bias를 줄일 수 있지만 constant step-size parameter(=$\alpha)$를 사용하면 시간이 지남에 따라 점진적으로 bias를 완화할 수 있다.

이런 전략은 초기 값을 어떻게 설정할지에 대해 조심스럽게 고려해야 하며 일반적으로 실제 상황에서는 0으로 세팅한다.

2.2 Markov Decision Process (MDPs)

MDP는 행동이 미래 결과 뿐만 아니라 즉각적인 보상에 영향을 미치는 순차적 의사 결정을 위한 프레임워크를 제공한다.

이때 MDP에서 즉각적인 보상은 delayed reward와 균형을 맞춘다.

각 행동 a의 값을 결정하는 것이 목표인 bandit problem과 달리 MDP는 상태 s에서 a 행위를 취하는 것의 가치(행동 가치 함수) 또는 s인 상태에 있는 것의 가치(행동 가치 함수)를 측정하는 것을 목표로 하며 최선(optimal) 행동이 취해지도록 가정한다.

MDP는 상태, 행동 그리고 보상으로 구성된다 $(\mathcal{S,A,R})$.

→에이전트가 실제 상호작용하는 요소들

시스템은 마르코프로 가정(즉, 행동의 결과는 과거 상태와 행동과 독립적임)하면서 오로지 현재 상태에만 의존한다.

마르코프 특성은 상태(state)가 미래 결과에 영향을 주는 과거 interaction 전체의 중요한 세부사항들을 포함해야 한다고 상태를 요구한다.

→의사 결정을 위한 정보가 현재 상태에 모두 포함되어야 한다.

또한, MDP의 역동성을 묘사하기 위해 상태 전이 행렬 함수 $p(s',r\ |\ s,a)$를 사용한다.

$p(s',r\ |\ s,a) = Pr\{\mathcal{S}t=s',\mathcal{R}t=r|\mathcal{S}{t-1}=s,\mathcal{A}{t-1}=a\}$

이어지는 상태 전이 확률, 상태-행동 그리고 상태-행동-다음 상태 triple rewards는 네 개의 인수를 가지는 dynamic function “p”로부터 도출 가능하다.

상태 전이 행렬
$p(s'|s,a)\equiv Pr\{\mathcal{S}t=s'|\mathcal{S}{t-1}=s,\mathcal{A}{t-1}=a\}=\Sigma{r\in\mathcal{R}}\ p(s',r|s,a)$
expected state-action pairs
$r(s,a)\equiv\mathbb{E}\{\mathcal{R}t|\mathcal{S}{t-1}=s,\mathcal{A}{t-1}=a\}=\Sigma{r\in\mathcal{R}}\ r\ \Sigma_{r \in \mathcal{R}}\ p(s',r|s,a)$
expected rewards for state-action-next-state triples
$r(s,a,s')=\mathbb{E}\{\mathcal{R}t|\mathcal{S}{t-1}=s,\mathcal{A}_{t-1}=a,\mathcal{S}t=s'\}=\Sigma{r\in\mathcal{R}}\frac{rp(s',r|s,a)}{p(s'|s,a)}$

MDP 프레임워크에서 목표 지향적 행동은 interaction을 통해 추상화된다.

→ 다시 말해, 복잡한 현실 세계의 학습 문제를 단순한 틀로 정리할 수 있다

또한, 어떠한 학습 문제든 에이전트와 환경 사이의 세 개의 시그널들(행동, 상태, 보상)로 축소될 수 있다.

에이전트는 미래 보상을 최대화할 방법을 찾지만 어떻게 수학적으로 이를 표현할 수 있을까?

$G_t$로 표현되는 return은 t스텝 이후에 받는 보상의 누적 합이다.

episodic task에 대해 다음과 같이 정의된다:

$\mathcal{G}t\equiv \mathcal{R}{t+1}+\mathcal{R}{t+2}+...+\mathcal{R}{\mathcal{T}}$

episodic 문제들은 에피소드라고 불리는 순차적으로 자연스럽게 나타나는 그들의 환경과 에이전트 사이에서의 상호작용이다(행맨 게임이 대표적인 예시).

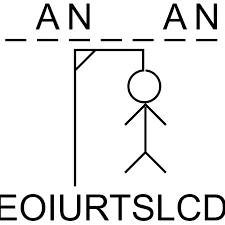
각 에피소드의 끝에서 표준 시작 상태가 복원된다.

반면 “continuing tasks”는 에피소드의 종결없이 지속적으로 유지되는 상호작용을 포함하는 태스크이다.

다시 말해, continuing task에서는 terminal state가 없기 때문에($\mathcal{T}=\infty$), continuing task의 return은 다르게 정의된다.

terminal state가 없는 continuing task에서 return $\mathcal{G}_t$는 미래 보상의 할인 합계로 정의된다.

$\mathcal{G}t\equiv\mathcal{R}{t+1}+\gamma\mathcal{R}{t+2}+\gamma^2\mathcal{R}{t+3}+...=\Sigma_{k=0}^\infty \gamma^k\mathcal{R}_{t+k+1}$

(여기서 $\gamma$는 0과 1사이의 할인율 의미)

$\gamma$가 1보다 작기 때문에 결국 유한한 값으로 수렴하게 되며 만약 0이라면 에이전트는 즉각적인 보상을 최대화하고자 하며 반대로 1에 가까워지면 미래 보상이 상대적으로 더 중요해지게 된다.

다음과 같이 위 식을 재귀적으로 표현할 수도 있다:

$\mathcal{G}t\equiv\mathcal{R}{t+1}+\gamma\mathcal{G}_{t+1}$

아래 수식은 episodic과 continuing task에서 모두 작동한다.

$\mathcal{G}t\equiv\Sigma{k=t+1}^\mathcal{T}\gamma^{k-t-1}\mathcal{R}_k$

2.3 Policies and Value Functions

가치 함수는 에이전트가 특정 상태에 있을 때(또는 특정 상태 내에서 행동을 수행할 때) 예상 return을 추정하는 함수이다.

가치 함수는 두 개의 큰 카테고리고 나눌 수 있다: “State Value Functions”, “Action Value Functions”

State Value Function은 policy $\pi$ 아래서 상태 s의 가치 함수인 $v_\pi(s)$는 s로 시작해서 정책을 따른 예상 return이다.

$v_\pi(s)\equiv\mathbb{E}\pi[\Sigma{k=0}^\infty \gamma^k\mathcal{R}_{t+k+1}|S_t=s]$

반면 Action Value Function은 정책 $\pi$ 아래서 상태 s에서 a 행동을 취하는 것의 가치는 $q_\pi(s,a)$이며 $\pi$를 따를 때 상태 s에서 시작하여 행동 a를 취했을 때의 예상 return이다.

$q_\pi(s,a)\equiv\mathbb{E}\pi[\mathcal{G}t|S_t=s,\mathcal{A}t=a]=\mathbb{E}\pi[\Sigma{k=0}^{\infty }\gamma^k\mathcal{R}{t+k+1}|S_t=s,\mathcal{A}_t=a]$

즉, q는 각 상태에서 취한 행동에 의존한다.

각 상태에 8개의 행동들과 10개의 상태가 있다면 80개의 함수가 필요한 반면 v는 오직 10개의 함수만 필요로 한다.

정책 $\pi$를 따르는 에이전트가 각 ‘상태’로부터의 returns를 평균화하면 그 평균은 $v_\pi(s)$로 수렴하며

각 ‘행동’으로부터의 returns을 평균화하면 $q_\pi(s,a)$로 수렴한다.

$v_\pi(s)$는 재귀적으로 다음과 같이 작성될 수 있다:

$v_\pi(s)\equiv\mathbb{E}\pi[\mathcal{G}t|\mathcal{S}t=s]=\mathbb{E}\pi[\mathcal{R}{t+1}+\gamma\mathcal{G}{t+1}|S_t=s]=\Sigma_a\pi(a|s)\Sigma_{s'}\Sigma_rp(s',r|s,a)[r+\gamma v_\pi(s')]$

(가장 우측 수식은 $v_\pi$에 대한 Bellman equation)

수식에서 알 수 있듯, 초기 state의 가치는 다음 상태 예측과 예상된 보상의 가치를 할인한 것과 동일하다.

$v_\pi(s)$와 $q_\pi(s,a)$는 강화학습에서 다른 목적을 가진다.

결정론적인 정책을 평가할 때 또는 특정 상태가 되는 것의 가치를 이해하는 것이 필요할 때, “state-value function”은 사용된다.

state-value 함수의 사용은 많은 action이 있을 때 유용한데 이는 그들이 오직 상태 가치의 평가만 필요로 함으로써 복잡성을 줄여주기 때문이다.

반면, action-value 함수는 같은 상태 내에서 다양한 행동들에 대한 잠재력을 비교하고 평가하는데 사용된다.

각 상태에서 가장 적절한 행동을 결정하는 것이 목표이며 행동 선택이 아주 중요하다.

action-value 함수는 다양한 행동들의 예상 return을 설명하며 그들은 특히 확률론적 정책이 있는 환경에서 유용하다.

게다가 연속 행동 공간을 다룰 때 action-value 함수는 행동의 영향에 대한 더 구체적인 이해를 제공할 수 있으며 동시에 정책 이행의 fine-tuning을 돕는다.

2.4 Optimal Policies and Optimal Value Functions

RL task를 해결하는 것은 장기 보상을 최대화하는 정책을 찾아내는 것이다.

가치 함수들은 정책들을 통한 부분적 서열을 만들며 예상 누적 보상을 기반으로한 비교와 순위를 만든다.

만약 $v_\pi(s)$≥$v_{\pi_0}(s)$라면 정책 $\pi$가 $\pi_0$보다 동일하거나 낫다

최적 정책 $\pi_*$은 다른 모든 정책들보다 낫거나 동등하며 동일한 최적 state-value function $v_*$을 공유하는데 이는 모든 가능한 정책들에 대한 최대 가치 함수로 정의된다.

$v_*(s)\equiv \max_\pi v_\pi(s)$

최적 정책은 또한 동일한 최적 action-value 함수 $q_*$을 공유하는데 이는 모든 가능한 정책들에 대한 최대 행동 가치 함수로 정의된다.

$q_*(s,a)\equiv \max_\pi q_\pi(s,a)$

최적 행동 가치 함수 $q_(s,a)$와 최적 상태 가치 함수 $v_(s)$ 사이의 관계는 다음 수식으로 정리된다.

$q_(s,a)=\mathbb{E}[\mathcal{R}{t+1}+\gamma v(\mathcal{S}_{t+1})|\mathcal{S}_t=s,\mathcal{A}_t=a]$

최적 행동 가치 함수 $q_(s,a)$에 의해 상태 가치 함수 $v_(s)$를 찾을 수 있다.

최적 가치 함수와 정책은 강화학습에서 최적의 상태를 나타낸다.

하지만 실질적인 한계점 때문에 계산적으로 많이 요구하는 태스크에서는 진실된 최적 정책을 찾기는 힘들다.

Dynamic Programming(DP)는 환경의 완벽한 모델을 가정하며 최적 가치를 찾도록 도와주는데 이는 실제 세계 케이스에는 적용하기 힘들다.

또한, DP 방법론은 이론적으로 좋음에도 sample efficient하지 않다.

→ 정확한 전이확률 $P(s'|s,a)$와 보상함수 $R(s,a)$를 안다고 가정하기 때문(기본적으로 많은 표본이 필요함)

최적 상태 가치 함수 $v_(s)$와 최적 행동 가치 함수 $q_(s,a)$에 대한 Bellman optimality equations은 아래와 같다.

$v_(s)=\max_a\mathbb{E}[\mathcal{R}{t+1}+\gamma v \mathcal{S}_{t+1}|\mathcal{S}t=s,\mathcal{A}t=a]=\max_a\Sigma{s',r}p(s',r|s,a)[r+\gamma v*(s')]$

$q_(s,a)=\mathbb{E}[\mathcal{R}{t+1}+\max{a'}q_( \mathcal{S}{t+1},a')|\mathcal{S}t=s,\mathcal{A}t=a]=\Sigma{s',r}p(s',r|s,a)[r+\gamma\max{a'} q*(s',a')]$

DP 알고리즘은 Bellman 수식을 update rule로 변환함으로써 파생된다.

$v_{k+1}(s) ← Σ_a π(a|s) Σ_{s',r} p(s',r|s,a)[r + γv_k(s')]$

2.5 Policy Evaluation (Prediction)

정책 평가 또는 예측은 주어진 정책 $\pi$에 대해 상태-가치 함수 $v_\pi$를 계산하는 것을 포한다.

이 과정은 각 상태로부터 정책 $\pi$를 따랐을 때 예상 return을 평가한다.

상태 가치 함수 $v_\pi(s)$는 상태 s로부터 시작하고 정책 $\pi$를 따르는 예상 return으로 정의된다.

$v_\pi(s)\equiv\mathbb{E}\pi[\mathcal{R}{t+1}+\gamma\mathcal{G}_{t+1}|\mathcal{S}_t=s]$

이는 재귀적으로 다음과 같이 표현된다.

$v_\pi(s)=\mathbb{E}\pi[\mathcal{R}{t+1}+\gamma v_\pi(\mathcal{S}{t+1})|\mathcal{S}t=s]=\Sigma_a\pi(a|s)\Sigma{s',r}p(s',r|s,a)[r+\gamma v\pi(s')]$

$v_\pi$의 존재와 유일성은 만약 $\gamma<1$이거나 모든 상태들이 $\pi$ 아래서 종료된다면 보장된다

DP 알고리즘 업데이트는 “expected updates”라고 불린다.

왜냐하면 그들은 단순히 샘플보다는 모든 잠재적 다음 상태들에 대한 예상에 의존하기 때문이다.

2.6 Policy Improvement

정책에 대한 가치 함수를 계산하는 목표는 향상된 정책들을 구별하는 것이다.

상태 s에 대한 결정론적 정책에 대한 $v_\pi$를 가정할 때 우리는 $a \ne \pi(s)$ 행동을 선택하도록 정책을 바꿔야 할까?

상태 $s(v_\pi(s))$로부터 존재하는 정책을 고수하는 효과성을 알지만 새로운 정책으로의 전환이 더 좋은 결과를 낳을 것인가?

이 질문에 대한 대답은 s에서 행동 a를 선택하고 $\pi$를 따름으로써 대답할 수 있다.

정책이 향상되는지 아닌지를 결정하기 위해 현재 정책에서 상태 s에서 다른 행동 a를 취하는 것의 가치를 비교한다.

이는 행동 가치 함수 $q_\pi(s,a)$를 사용하여 확인할 수 있다.

$q_\pi(s,a)\equiv\mathbb{E}[\mathcal{R}{t+1}+\gamma v\pi(\mathcal{S}_{t+1})|\mathcal{S}t=s,\mathcal{A}t=a]=\Sigma{s',r}p(s',r|s,a)[r+\gamma v\pi(s')]$

핵심 평가기준은 이 가치가 $v_\pi(s)$를 뛰어넘는가 아닌가이다.

만약 $q_\pi(s,a)>v_\pi(s)$라면 s에서 행동 a를 선택하는 것이 $\pi$를 따르는 것보다 지속적으로 더 이득이며 이는 더 향상된 정책 $\pi'$을 산출한다.

→a를 선택한 이후에 정책 $\pi$를 따르는 것이 단순히 정책 $\pi$을 따르는 것보다 더 좋다면 지금 정책이 비효율적이라는 말이므로

2.7 Policy Improvement Theorem

정책 향상 이론은 모든 상태 s에 대해 $q_\pi(s,\pi'(s))\ge v_\pi(s)$이라면 새로운 정책 $\pi'$은 최소한 기존 정책 $\pi$만큼 좋은 것이다.

이를 수식화하면:

$q_\pi(s,\pi'(s))\ge v_\pi(s)$

만약 $\pi'$이 더 크거나 같은 예상 return을 모든 상태에서 달성한다면 다음과 같다:

$v_{\pi'}(s) \ge v_\pi(s)$

만약 어떠한 상태든 엄격한 inequality가 존재한다면 $\pi'$는 $\pi$보다 뛰어나다.

새 정책 $\pi'$은 행동 가치 함수 $q_\pi(s,a)$를 최대화하는 행동을 선택함으로써 획득될 수 있다.

$\pi'(s)\equiv\arg\max_a q_\pi(s,a)=\arg\max_a\mathbb{E}[\mathcal{R}{t+1}+\gamma v\pi(\mathcal{S}_{t+1})|\mathcal{S}t=s,\mathcal{A}t=a]=\arg\max_a \Sigma{s',r}p(s',r|s,a)[r+\gamma v\pi(s')]$

정책 향상은 가치 함수를 기반으로한 greedy 접근을 선택함으로써 초기 정책을 강화하는 새 정책을 만든다.

$\pi'$가 $\pi$만큼 동등하게 효과적이지만 뛰어나지는 않다고 가정하면 $v_\pi=v_{\pi'}$는 이를 모든 상태 s에 대해 보장한다.

최적 상태 가치 함수 $v_(s)$와 최적 행동 가치 함수 $q_(s,a)$ 사이의 관계는 다음 수식을 따른다.

$v_{\pi'}(s)=\max_a\mathbb{E}[\mathcal{R}{t+1}+\gamma v{\pi'}(\mathcal{S}_{t+1},)|\mathcal{S}t=s,\mathcal{A}t=a]=\max_a\Sigma{s',r}p(s',r|s,a)[r+\gamma v{\pi'}(s')]$

정책 향상은 초기 정책이 이미 최적이지 않다면 더 나은 정책을 산출한다.

이 컨셉은 확률론적 정책으로 확장할 수 있다.

확률론적 정책은 행동들에 대한 일련의 확률들을 도입하며 동시에 가장 높은 확률을 보이는 greedy policy와 함께 나열된 행동을 보인다.

2.8 Policy Iteration

policy iteration은 policy evaluation과 policy improvement 사이의 반복을 통해 향상된 정책과 가치 함수를 얻으면서 진행된다.

주어진 유한한 MDP에 대해 반복적인 과정이 최적의 정책과 가치 함수로 수렴된다.

이 방법을 Policy Iteration이라고 한다.

Policy Iteration은 두 과정을 포함한다: 현재 정책을 따르는 가치 함수를 정렬하는 정책 평가 그리고 가치 함수를 기반으로 정책을 greedier하게 만드는 policy improvement

2.9 Value Iteration

Policy Iteration의 한계는 각 반복이 정책 평가를 요구하며 동시에 종종 전체 상태 집합을 여러 번 통과해야 한다.

이를 다루기 위해 정책 평가는 수렴에 대한 확신을 잃지 않으며 간략화될 수 있다.

이 방법은 value iteration으로 단일 sweep 이후 정책 평가를 제거한다.

이 방법은 정책 평가의 절단된 형태로 정책 향상을 결합한다.

$v_{k+1}(s)\equiv\max_a\mathbb{E}[\mathcal{R}{t+1}+\gamma v_k(S{t+1})|S_t=s,\mathcal{A}t=a]=\max_a\Sigma{s',r}p(s',r|s,a)[r+\gamma v_k(s')]$

value iteration에서 핵심 이점은 이것의 효율성이다.

이 방법은 정책 평가와 향상을 단일 업데이트 단계로 병합함으로써 계산에 대한 짐을 줄여준다.

이 방법은 특히나 매 스텝에서의 policy iteration의 전체 정책 평가가 계산적으로 막대한 큰 state spaces에 유용하다.

추가적으로 value iteration은 모든 상태 가치들이 동시에 업데이트되는 동기화된 업데이트 접근을 사용하거나 상태 가치들이 한 번에 하나씩 업데이트되어 실제로 더 빠르게 수렴될 수 있는 비동기적 업데이트 접근을 사용하여 실행된다.

value iteration의 다른 주목할만한 점은 초기 상태에 대한 robustness이다.

임의의 가치 함수에서 시작하여 value iteration은 반복적으로 수렴할 때까지 가치 값을 재정의하는데 이는 초기 정책이 최적의 정책과 멀 때에도 최적의 정책을 찾기 위한 reliable한 방법이다.

추가로 이어지는 bootstrapping(상태의 가치가 연속되는 다음 상태의 추정된 가치를 기반으로 업데이트됨)의 원리를 묘사함으로써 value iteration은 더 발전된 알고리즘을 위한 근간을 제공한다.

이 원칙은 역동적이고 불확실한 환경에서 exploration과 exploitation의 균형을 찾기 위한 많은 강화학습 알고리즘에 핵심이다.

3 Core RL Methods

3.1 Model-free & Model-based methods

Model-free 방법론은 환경의 모델 구축 없이 최적 정책이나 가치 함수를 직접적으로 결정하는 것이다.

이 방법론은 관측된 상태, 행동 그리고 보상으로부터 완전히 학습하기 때문에 전환 확률이나 보상에 대한 지식이 필요 없다.

model-based methods와 비교하면 model-free 방법론은 실행하기 쉽고 동시에 경험 기반의 학습에 의존한다.

Value-based와 Policy-based 2가지 방법으로 분류할 수 있는데

전자는 최적의 정책을 얻기 위해 action-value 함수를 학습하는데 집중한다.

두 방법 모두 수렴할 때까지 Bellman equation을 기반으로 그들의 action-value 추정치를 업데이트한다.

이러한 접근법들은 예상 보상의 gradient를 따라감으로써 정책 파라미터를 직접적으로 조정한다.

이 접근은 특히 가치 기반 접근법이 효과적이지 않은 고차원 행동 공간이 있는 환경에서 유용하다.

정책 기반 접근법은 확률론적 정책을 다룰 수 있고 동시에 행동 선택에서 불확실성을 다루는 자연스러운 프레임워크이다.

추가로 가치 기반 접근법과 정책 기반 접근법을 혼합한 hybrid 접근법이 있다(Actor-Critic 알고리즘).

이 접근법들은 두 가지 핵심 요소들로 구성된다: 정책 파라미터를 cirtic에 의해 제안된 방향으로 업데이트하는 actor와 action-value function을 평가하는 cirtic

두 학습의 유형을 혼합하는 것은 더 안정적이고 효과적인 학습을 제공하고자 하는 것이다.

또 다른 model-free 방법론에서의 발전은 Deep RL(DRL)의 개발이다.

전통적 강화 학습 알고리즘과 인공 신경망을 결합함으로써 Deep Q-Networks (DQN)과 Proximal Policy Optimization (PPO)와 같은 방법론들은 복잡하고 고차원 환경(게임, 로봇 통제 태스크 등)에서 높은 성공을 이뤄냈다.

모델 기반 방법론을 사용하여 행동의 결과를 예측하는 것이 가능하며 이는 전략적 계획과 의사 결정을 촉진한다.

이러한 방법론들의 사용은 정확한 모델의 개발과 정의의 복잡성에도 불구하고 가상 실험에 대한 기회를 제공함으로써 학습 효율성을 강화할 수 있다.

자율 주행차는 어떻게 모델 기반 방법론이 실제 세상에 사용되는 지에 대한 예시이다.

자율 주행이 동적인 환경에서 주행할 때, 방해물 회피, 그리고 최적의 길 찾기를 실행해야 한다.

자율주행차는 그들의 환경의 디테일한 모델을 생성한다.

이러한 모델들은 정적 요소(도로, 건물) 뿐만 아니라 동적 요소(다른 차량, 보행자)를 포함한다.

센서 데이터(카메라, LIDAR, 레이더)가 이 모델을 구축하기 위해 사용한다.

환경 모델의 사용을 통해 차량은 다양한 행동의 결과를 예측할 수 있다.

예를 들어 차량 노선을 변경할 때 안전하고 효율적으로 하기 위해 모델이 주위 차량들의 행동을 예측한다.

모델 기반의 접근법은 그렇지 않은 접근법에 비해 몇가지 장점들이 존재한다.

미래 상태와 보상을 시뮬레이션함으로써 환경과 직접적인 소통없이 다양한 행동 시퀀스들을 계획하고 평가할 수 있다.

이는 최적의 정책으로의 빠른 수렴을 돕는다(모델의 예측을 활용하기 때문).

모델 기반 접근법은 환경의 변화에도 빠르게 적응 가능하다(업데이트하고 그에 따른 재 계획이 가능하기 때문).

그러나 몇가지 문제점들도 있는데 바로 정확도와 계산 비용이다.

환경의 정확한 모델을 만들기 위해서는 high-fidelity model이 필요하다.

→High fidelity model: 높은 실제 재현 모델

또한, 계획 과정이 매우 계산적으로 비싼데 특히 많은 상태와 행동이 있는 환경에서 더 그렇다.

3.2 Off-Policy and On-Policy Methods

On-policy와 off-policy 학습은 model-free 학습 접근법 내의 방법론이다.

즉 환경 변환 확률에 의존하지 않는다.

이 둘은 행동 정책과 업데이트된 정책 사이의 관계를 기반으로 분류된다.

On-policy 방법은 탐구와 학습을 연결하기 위해 의사 결정을 내리기 위해 사용된 정책을 평가하고 향상시킨다.

이러한 방법들은 취해진 행동과 현재 정책를 따르는 동안 받은 보상을 기반으로 정책을 업데이트한다.

이는 exploration과 정책 향상이 자연스럽게 통합된 일관성 있는 학습 과정을 진행하며 최적화된 정책이 환경과 소통하는데 사용된 것이라는 것을 보증한다.

핵심 개념 정리

의사결정에 사용하는 정책(policy)과 학습하는 정책이 동일한 방법
에이전트가 현재 따르고 있는 정책 π를 직접 평가하고 개선
탐색(exploration)과 학습이 자연스럽게 통합됨

Off-policy 방법은 반면 에이전트의 행동과 무관하게 최적 정책의 독립적인 가치를 학습한다.

그에 따라 두 부류의 정책을 구분 가능하다: behavior policy(b) & target policy($\pi$)

behavior policy는 환경을 탐색하는 반면 target policy는 수집된 경험을 기반으로 성능을 향상시킨다.

어떠한 정책에 의해 생성된 데이터로부터 학습이 가능하다는 장점이 있다.

Behavior policy는 exploration과 exploitation의 균형을 맞추면서 어떻게 환경을 탐색할까를 결정한다.

target policy는 어덯게 에이전트가 추정 값을 향상시키기 위해 이러한 경험들로부터 학습할 수 있을까를 결정한다.

on-policy에서는 behavior policy와 target policy가 동일하다

→ off-policy는 행동이 달라져도 그 경험을 가지고 성능을 향상

핵심 개념 정리

행동 정책(behavior policy, b)과 목표 정책(target policy, π)이 다른 방법
행동 정책: 환경을 탐색하며 데이터를 수집
목표 정책: 수집된 경험을 바탕으로 최적 성능을 목표로 학습
더 유연하고 샘플 효율적임(다만 unstable할 수 있음)

4. Essential Algorithms

4.1 Value-based

Q-Learning

Model-free, Off-policy 알고리즘 (+Temporal Difference)
상태-행동 가치 함수 Q(s,a)를 학습
업데이트 규칙:
Q(s,a) ← Q(s,a) + α[r + γ max Q(s',a') - Q(s,a)]
예시: 미로 탈출 게임에서 각 위치(상태)에서 각 방향(행동)으로 갈 때의 예상 보상을 학습

DQN (Deep Q-Networks)

Q-Learning + 신경망
원시 픽셀 입력에서 직접 학습 가능
Experience Replay: 과거 경험을 저장하고 무작위로 샘플링하여 학습
예시: 아타리 게임을 화면 픽셀만 보고 플레이 학습

4.2 Policy-based (정책 기반) 알고리즘

REINFORCE

정책을 직접 최적화
정책 경사(Policy Gradient) 방법 사용
업데이트 규칙:
θ ← θ + α∇log π(a|s)G_t
예시: 로봇 팔이 연속적인 각도 조절을 통해 물체를 잡는 방법 학습

PPO (Proximal Policy Optimization)

TRPO의 단순화 버전
정책 업데이트 크기를 제한하여 안정적 학습
예시: 자율주행차가 급격한 조향 변경 없이 점진적으로 운전 스타일 개선

4.3 Hybrid (Actor-Critic) 알고리즘

A2C/A3C

Actor: 행동을 선택하는 정책
Critic: 행동의 가치를 평가
Advantage 함수 사용: A(s,a) = Q(s,a) - V(s)
예시: 체스 AI에서 Actor는 다음 수를 제안하고, Critic은 그 수의 좋고 나쁨을 평가