[2025-1] 최민서 - SDEDIT: Guided Image Synthesis and Editing with Stochastic Differential Equations

[논문링크] https://arxiv.org/abs/2108.01073

SDEdit: Guided Image Synthesis and Editing with Stochastic Differential Equations

 

SDE Diffusion 논문을 읽지 않았다면 본 논문을 이해하기 어려울 수 있다.

[SDE Diffusion 논문리뷰] https://outta.tistory.com/270

[2025-1] 최민서 - Score-based Generative Modeling through Stochastic Differential Equations

 

1. Introduction

 

본 논문에서는 제공된 가이드 이미지를 바탕으로 가이드와 유사하면서도 품질이 좋은 이미지를 생성하는 방법을 소개한다. 가이드 이미지란 원본 이미지의 픽셀값을 변화시켜 원본 이미지의 일부 정보만을 가진 이미지이다. 사람이 손으로 스케치한 이미지, 원본 이미지의 패치가 제거된 이미지, 사람 얼굴 이미지에 안경을 그려 넣은 이미지 등이 가이드 이미지의 예시이다.

 

이러한 태스크를 guided image synthesis(editing)이라 하는데, 기존의 방법론은 크게 두가지로 나뉜다. 두 방법은 각각 conditional GAN, GAN inversion을 활용하는 방식으로, 두 방식모두 새로운 editing task마다 모델을 학습시켜야 하기 때문에 비효율적이다.

 

본 논문에서는 SDEdit(Stochastic Differential Editing) 방법을 소개한다. 학습된 SDE Diffusion 모델을 이용하며, 태스크마다 따로 학습이 필요하지 않다. SDEdit에서는 제공된 가이드 이미지에 노이즈를 추가하여 하이퍼파라미터로 설정된 $t_0 \in (0,1]$ 시점부터 reverse SDE를 진행한다. 

 

2. Background

 

SDE diffusion 모델에 대한 이해가 필요하다. Diffusion 모델의 forward process와 reverse process를 SDE를 통해 나타낼 수 있다.

 

$$ \mathbf{x}(t) = \alpha(t)\mathbf{x}(0) + \sigma(t)\mathbf{z}, \;\; \mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) $$

 

이 때 $t \in (0,1]$이다. $\sigma(t)\,:\,[0,1] \rightarrow [0,\infty)$는 노이즈 $\mathbf{z}$의 크기를 나타내는 스칼라 함수이고, $\alpha(t)\,:\,[0,1]\rightarrow [0,1]$은 데이터 $\mathbf{x}(0)$의 크기를 나타내는 스칼라 함수이다.

 

VE-SDE에서는 모든 $t$에 대하여 $alpha(t)=1$이고 $\sigma(1)$은 매우 큰 값을 가지고 확률분포 $p_1$이 $\mathcal{N}(\mathbf{0},\sigma^2(\mathbf{1})\mathbf{I})$에 근접하게 된다. VP-SDE는 모든 $t$에 대해 $\alpha^2(t)+\sigma^2(t)=1$를 만족하고 확률분포 $p_1$은 $\mathcal{N}(\mathbf{0},\mathbf{I})$에 근접하게 된다.

 

이후 나오는 본 논문의 설명은 VE-SDE를 기준으로 한 것이며, VP-SDE에 대해서도 비슷한 논의를 할 수 있다. VP-SDE에 관한 자세한 논의는 논문의 Appendix C에 나와있다.

 

VE-SDE의 경우 아래의 reverse SDE를 풀어 샘플링 할 수 있다.

 

$$ d\mathbf{x}(t) = \left[ -\frac{d[\sigma^2(t)]}{dt}\nabla_{\mathbf{x}} \mathrm{log}p_t(\mathbf{x}) \right]dt + \sqrt{\frac{d[\sigma^2(t)]}{dt}}d\bar{\mathbf{w}} $$

 

실제로는 score 모델이 아래의 training objective을 따라 학습된다.

 

$$ L_t = \mathbb{E}_{\mathbf{x}(0) \sim p_{data}, \mathbf{z} \sim \mathcal{N}(\mathbf{0},\mathbf{I}) }[\Vert \sigma_t \mathbf{s}_\theta(\mathbf{x}(t),t) - \mathbf{z} \Vert_2^2] $$

 

학습된 score 모델을 이용하여 위의 reverse SDE를 Euler-Maruyama method를 이용하여 아래와 같이 풀 수 있다.

 

$$ \mathbf{x}(t) = \mathbf{x}(t+\nabla t) + (\sigma^2(t) - \sigma^2(t+\nabla t)) \mathbf{s}_\theta (\mathbf{x}(t),t) + \sqrt{\sigma^2(t)-\sigma^2(t+\nabla t)} \mathbf{z} $$

 

3. Gudied Image Synthesis and Editing with SDEdit

 

먼저 Guided image synthesis 모델의 성능을 평가하기 위한 두가지 기준을 소개한다.

 

1) Realism

이미지가 얼마나 실제와 유사한지를 나타낸다. 일반적으로 생성형 모델이 성능이 좋다는 것은 realism이 높은 이미지를 만들어 낸다는 것이다. Realism은 KID score등을 통해서 측정될 수 있다. 

 

2) Faithfulness

이미지가 얼마나 가이드 이미지와 유사한지를 나타낸다. 가이드 이미지와 생성된 이미지와의 $L_2$ norm을 측정하는 등의 방식을 이용하여 측정될 수 있다.

 

두 성능 지표는 양의 상관관계를 갖지는 않는다. Realism이 높지만 faithfulness가 낮은 이미지(랜덤 노이즈로부터 생성된 이미지)가 있을 수 있고, faithfulness가 높지만 realism이 낮은 이미지(가이드 이미지)가 있을 수 있기 때문이다.

 

Reverse SDE는 $t=1$부터 $t=0$까지 역순으로 풀리게 되어 있지만, 꼭 $t_0=1$에서 reverse process가 시작할 필요는 없다. SDEdit에서는 가이드 이미지를 입력으로 받으면, $t_0 \in (0,1)$의 시작 시점을 정한 뒤, $\mathcal{N}(\mathbf{x}^{(g)} ; \sigma^2(t_0)\mathbf{I})$로부터 $\mathbf{x}^{(g)}(t_0)$를 샘플링한다. 샘플링된 $t_0$ 시점의 이미지로부터 reverse process를 진행해 노이즈가 제거된 이미지 $\mathbf{x}_0$를 얻는다.

 

SDEdit에서 중요한 하이퍼파라미터는 $t_0$이다. 높은 realism과 faithfulness를 갖는 최적의 $t_0$를 찾아야 한다. 하지만 일반적으로 $t_0$에 대해, realism과 faithfulness는 trade-off 관계이다.

 

$t_0$의 값이 1에 가까울수록, reverse process의 과정이 길어지므로, 가이드 이미지와는 거리가 멀지만, 보다 실제적인 이미지가 생성된다. 반면 $t_0$의 값이 0에 가까울수록, reverse process의 과정이 짧아지므로, 실제적이진 않지만 보다 가이드 이미지와 유사한 이미지가 생성된다.

 

위 그림에서도 볼 수 있듯이 $t_0$의 값이 커질수록 실제적인 이미지가, 작아질수록 가이드에 가까운 이미지가 생성된다. 논문에서는 실험을 통해 적절히 주어진 가이드 이미지의 경우, $t_0$의 값은 0.4~0.6 정도가 적절하다고 설명한다. 

 

이에 대한 수학적인 설명은 아래와 같다.

 

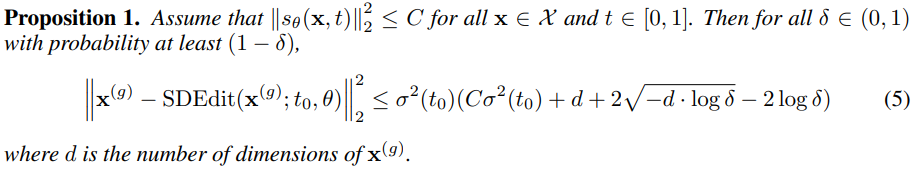
자세한 증명은 논문의 Appendix A에 나와있다.

 

$SDEdit(\mathbf{x}^{(g)} ;t_0,\theta)$은 가이드 이미지 \mathbf{x}^{(g)}를 $t_0$ 시점부터 reverse process 진행하여 얻은 노이즈가 제거된 이미지를 의미한다.

 

위 proposition에서 볼 수 있듯이 $t_0$의 값이 커질수록 가이드 이미지와 생성된 이미지의 차이가 커진다. 즉 위 proposition으로부터 $t_0$의 값이 커질수록 realism이 증가하지만, faithfulness는 감소함을 알 수 있다.

 

SDEdit의 자세한 알고리즘은 아래와 같다.

 

4. Experiments

 

이제 실험을 통해, SDEdit 방식이 기존의 GAN을 이용한 방식보다 성능이 좋음을 검증한다. 특정 태스크들에 대해 SDEdit의 성능을 측정해보기 전에, 평가 지표에 대해 정리해보자.

 

1) Realism

- Kernel Inception Score(KID)를 이용하여 생성된 이미지와 실제 이미지와의 차이를 비교한다.

- MTurk 조사를 통해 이미지가 얼마나 실제와 같은지 측정한다.

 

2) Faithfulness

- 가이드 이미지와 생성된 이미지와의 $L_2$ norm을 측정한다.

- LPIPS 점수를 측정한다.

- MTurk 조사를 통해 이미지가 얼마나 가이드와 유사한지 측정한다.

 

4.1 Stroke-Based Image Synthesis

 

먼저 LSUN 데이터셋에서 사람이 그린 스트로크 이미지(간단히 색칠만 한 이미지)를 가이드 이미지로 제시했을 때 각 모델별 성능을 비교했다.

 

MTurk는 Amazon Mechanical Turk의 사용자들이 SDEdit가 생성한 이미지가 다른 모델이 생성한 이미지보다 좋다고 응답한 비율이다. 위 표에서 볼 수 있듯이 모든 지표에서 SDEdit이 월등히 좋은 성능을 보인다.

 

아래 표는 알고리즘에 따라 생성한 스트로크 이미지를 가이드 이미지로 제시했을 때 각 모델별 성능을 비교했다.

 

위의 두 표에서 확인할 수 있듯이, 스트로크 가이드 이미지 태스크에서 SDEdit가 realism, faithfulness 모두 훨씬 좋은 이미지를 생성함을 알 수 있다. Realism과 faithfulness를 합한 전체적인 satisfaction 점수 MTurk 방식으로 측정했을 때, 다른 GAN 기반 모델 대비 SDEdit 방식이 realism 점수에서 80%, 전체 satisfaction 점수에서 75% 앞섰다.

 

실험의 세부사항은 논문의 Appendix C, E에 나와있다.

 

4.2 Flexible Image Editing

 

SDEdit은 image editing task에서도 기존의 GAN 기반 모델보다 좋은 성능을 보인다.

 

1) Stroke-based image editing

 

진짜 이미지에 스트로크 edit을 추가한 가이드 이미지를 제시했을 때, 주어진 edit에 따라 적절히 원본 이미지를 변형하는 것이 stroke-based image editing이다. 

 

위 그림에서 볼 수 있듯이, stroke-based image editing task에서도 SDEdit가 기존 GAN 기반 모델들보다 우수한 성능을 보임을 확인할 수 있었다. SDEdit에 의해 생성된 이미지는 realism, faithfulness 모두 높았다.

 

2) Image compositing

 

원본 이미지에 다른 이미지의 특성 픽셀을 붙임으로써 두 이미지를 합칠 수 있는데, 이 때 두 이미지가 자연스럽게 어우러지도록 만드는 것이 image compositing task다. 

 

위의 그림과 표에서 확인할 수 있듯이 SDEdit은 image compositing task에서도 좋은 성능을 보인다. 

 

실험의 세부사항은 논문의 Appendix C, E에 나와있다.

 

5. Conclusion

 

Stochastic Differential Editing(SDEdit)은 가이드 이미지에 노이즈를 추가한 뒤 특정 시점 $t_0$로부터 reverse process를 진행하여 이미지를 생성한다. SDEdit은 별도의 추가 훈련 없이 훈련된 SDE Diffusion 모델만으로 여러 독립된 task를 수행할 수 있다. SDEdit을 통해 생성된 이미지는 realism, faithfulness의 관점에서 기존의 GAN 기반 모델들보다 월등함을 실험적으로 확인할 수 있었다.