[2025-1] 차승우 - LONG SHORT-TERM MEMORY
https://www.bioinf.jku.at/publications/older/2604.pdf
0. Abstract
1. LSTM 출현 배경
- 기존의 순환 신경망(RNN)은 긴 시간 간격에 걸친 정보를 학습하기 어렵습니다.
- Gradient Vanishing
2. LSTM
1. Constant Error Carousel
- 특정 유닛 내에서 오류 신호가 사라지지 않고 일정하게 유지되도록 설계된 구조
2. Gate
- 게이트를 통해 정보를 선택적으로 저장 및 삭제, 계산
3. 실험 결과
1. RNN의 장기 의존성 문제 해결
1. Introduction
1. 순환신경망
- 순환 신경망은 피드백을 통해 단기 기억 형태로 저장할 수 있으나, 단기 기억에 무엇을 저장할지를 학습하는 알고리즘은 시간이 오래 걸리거나 성능이 좋지 않다. 입력과 학습 신호 사이의 시간 간격이 긴 경우에는 문제가 심각해진다.
2. 순환신경망의 문제점
1. Gradient Explode
- 전파되는 오류 신호가 지나치게 커져 가중치가 불안정
2. Gradient Vanishing
- 오류 신호가 점점 약해져 학습이 오래 걸리거나 실패
3. LSTM
1. 긴 시간 간격에서도 오류 신호를 일정하게 유지
2. 내부 상태에서 오류 신호를 일정하게 유지
3. 짧은 시간 간격에서도 학습 가능
2. Previous work
1. 그래디언트 하강법 변형(Gradient-Descent Variants)
- BPTT 및 RTRL과 동일한 문제(오류 폭발과 소멸)를 겪음
2. 시간 지연(Time-Delays)
- Lang et al.(1990)의 Time-Delay Neural Networks(TDNN) 및 Plate(1993)의 방법은 짧은 시간 간격에서만 실용적
3. 시간 상수(Time Constants)
- Mozer(1992)는 시간 상수를 사용해 장기 시간 간격 문제를 해결하려 했지만, 시간 상수는 외부에서 미세 조정이 필요
4. Ring의 접근법
- Ring(1993)은 긴 시간 간격 문제를 해결하기 위해 유닛에 추가적인 고차 유닛을 도입했으나, 추가 유닛의 도입의 문제
- 이러한 연구 외에도 여러 연구들이 RNN이 가진 시간 간격 문제에 대해 해결하려고 접근했으나, 사용 범위가 존재하거나 조건이 까다로움
- LSTM은 기존 연구들과 달리 긴 시간 간격에서도 안정적으로 학습할 수 있는 구조와 효율적인 학습 알고리즘을 제공
3. CONSTANT ERROR BACKPROP
3.1 EXPONENTIALLY DECAYING ERROR
1. BPTT(Backpropagation Through Time)
특정 시점 t에서 출력 유닛 k의 출력 오류
$$v_{k}(t)\,=\,f_{k}'(net_{k}(t))(d_{k}(t)-y^{k}(t))$$
$d_{k}(t)$ : 출력 유닛 k의 목표값
$$y^{i}(t)\,=\,f_{i}(net_{i}(t))$$
$y^{k}(t)$ : 출력 유닛 k의 실제 출력
$$net_{i}(t)\,=\,\sum w_{ij}y^{j}(t-1)$$
$net_{k}(t))$ : 유닛 k로 들어오는 총 합
- 히든 유닛j의 오류 신호
$$v_{j}(t)\,=\,f_{j}'(net_{j}(t))\sum_{i}^{}w_{ij}v_{i}(t+1)$$
2. Hochreiter의 분석( 오류 전파가 지수적으로 감소하거나 폭발하는 이유 )
- Hochreiter(1991)의 분석에 따르면, 오류가 유닛 간에 전파될 때 다음과 같은 방식으로 전파된다.
- 유닛 u에서 유닛 v로 q 단계 전파된 오류는 다음과 같이 정의
$$ \frac{\partial v_{v}(t-q)}{\partial v_{u}(t)}\,=\,\begin{cases}
& f_{v}'(net_{v}(t-1)w_{wv})\,(q\,=\,1) \\
& f_{v}'(net_{v}(t-1)\sum_{l=1}^{n}\frac{\partial v_{l}(t-q+1)}{\partial v_{u}(t)}w_{lv})\,(q\,>\,1)
\end{cases}$$
3. 결론
$$||f_{lm}'(net_{lm}(t-m)w_{lm}l_{m-l})\|>1.0$$
- 오류가 지수적으로 커져 학습이 불안정해지고, 가중치가 비정상적으로 커집니다.
$$||f_{lm}'(net_{lm}(t-m)w_{lm}l_{m-l})\|<1.0$$
- 오류가 단계별로 감소하며 지수적으로 축소됩니다. 이는 오래된 시점의 정보가 유실되어 RNN이 장기 의존성을 학습할 수 없게 된다.
- 기존 알고리즘은 오류가 시간이 지남에 따라 감소하여 장기적 상호작용을 학습할 수 없다,
- BPTT는 긴 시간 간격 문제를 해결하기 위해 설계된 방법이 아님. 이를 해결하기 위해 다른 아키텍처(LSTM 등)가 필요
4. Global Error Flow(with Local Error flow)
- 위의 전개된 지역 오류의 확장으로써 전역 오류 흐름 또한 사라진다는 것을 알 수 있다.
- 로컬 오류 흐름과 글로벌 오류 흐름 모두 시간이 지남에 따라 지수적으로 감소할 수 있습니다. 특히, 활성화 함수와 가중치 크기에 따라 오류 전파의 감소가 더욱 심화
- 로지스틱 시그모이드 함수는 오류 전파의 감소를 가속화하여 결과적으로 BPTT는 긴 시간 간격의 문제를 효과적으로 처리하지 못한다.
3.2 CONSTANT ERROR FLOW: NAIVE
1. 단일 오류 흐름 유지
- 단일 유닛 j에서 오류 흐름이 일정하도록 하기 위해, 다음의 조건이 필요
$$f_{j}'(net_{j})w_{jj}=1.0$$
2. CEC 매커니즘
- 상수 오류 회전목마(CEC)는 LSTM 셀이 오류 신호를 시간적으로 전달하면서도 그 크기를 유지하는 메커니즘
- LSTM이 장기 의존성을 처리할 수 있도록 하는 핵심 개념
- CEC는 LSTM 셀의 한 부분인 셀 상태(Cell State)의 핵심 원리로써,
1. CEC
$$f_{j}(net_{j}(t))\,=\,w_{jj}*net_{j}(t)$$
2. 선형 활성화 함수
- CEC를 구현하려면 $f_{j}(x)$가 선형이어야 한다.
$$f_{j}\,=\,x$$
- 선형 활성화 함수의 특성 덕분에, 입력값이 그대로 출력으로 전달된다. 이를 통해 유닛의 상태값이 변형 없이 유지
3. 가중치 조건
- CEC의 또 다른 중요한 조건은 $w_{jj}$가 1.0으로 설정
- 이 가중치 조건과 선형 활성화 함수의 조합으로 인해 유닛의 활성화 값 $y_{j}(t)$는 시간에 따라 다음과 같이 유지
$y_{j}(t+1)=f_{j}(net_{j}(t+1))=w_{jj}*net_{j}(t+1)=net_{j}(t+1)=y_{j}(t)$
- 유닛 j의 활성화 값$y_{j}(t)$은 항상 동일하게 유지된다.
- 이는 장기 정보의 저장이 가능해지며, 셀 상태가 시간에 따라 변하지 않고 일정하게 유지하도록 합니다. 게이트와 함께 사용되어 기억을 유지&변환한다.
4. CEC와 셀 상태
1. CEC
- 셀 상태가 시간적으로 오류 신호를 유지하는 메커니즘에 대한 이론적 원리
2. 셀
- LSTM 셀의 실제 데이터 구조로, 정보를 저장하고 전달하는 역할
- 셀 상태는 CEC 원리에 기반해 설계되었지만, 입력 게이트와 망각 게이트의 영향을 받아 동적으로 변할 수 있다.
3. 게이트
1. Input Gate
- 새로운 정보를 셀 상태에 얼마나 추가할지 결정
2. Forget Gate
- 기존 정보를 얼마나 유지할지 결정
3. Output Gate
- 셀 상태 정보를 출력으로 얼마나 보낼지 결정
4. LONG SHORT-TERM MEMORY
1. 메모리 셀과 게이트 유닛 (Memory Cells and Gate Units)
- 기존 CEC(상수 오류 회전목마)의 단점을 극복하기 위해, 새로운 구조를 설계
1. Input Gate Unit
- 특정 정보를 메모리에 저장할 때, 불필요한 입력으로부터 메모리 내용을 보호
2. Output Gate Unit
- 메모리에 저장된 현재 관련 없는 정보가 다른 유닛에 영향을 주는 것을 방지
2. 메모리 셀의 구조


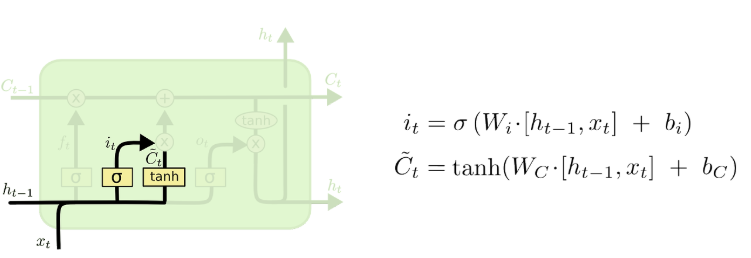
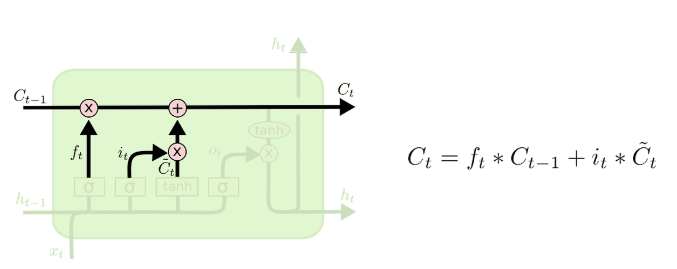

3.오류 신호와 CEC
1. CEC 내부 오류 신호
2. 게이트 유닛
4. LSTM 구조
1. 구성
- 입력층, 은닉층, 출력층으로 구성
2. 은닉층
- 메모리 셀 및 게이트 유닛
- 은닉층의 모든 유닛은 상위층의 모든 유닛으로 연결될 수 있다.
5. 학습 방식
1. RTRL 변형
- 입력/출력 게이트의 곱셈적 동작을 고려한 RTRL 변형 알고리즘 사용
2. 오류 전파 방식
- 메모리 셀 내부에서는 오류가 무한히 뒤로 전파될 수 있지만, 입력 게이트와 출력 게이트를 거치면 한 번 스케일링되어 가중치 변경에 사용됨
6. 계산 복잡도
- 업데이트 복잡도는 O(W), 가중치의 개수에 따라 달라진다.
7. LSTM의 문제점
1. Abuse Problem
1. Problem
1. 초기 학습 단계에서 네트워크는 메모리 셀을 bias에 남용할 수 있다.
2. 두 개의 메모리 셀이 동일한 중복 정보를 저장하는 경우
2. Solution
1. 순차 네트워크 구성법
- 에러 감소가 멈추면 새로운 메모리 셀과 게이트 유닛을 네트워크에 추가
2. 출력 게이트 바이어스
- 출력 게이트에 음의 초기 바이어스를 적용하여 메모리 셀의 초기 활성화를 0에 가깝게 유지
- 바이어스가 더 큰 음수인 셀은 학습 과정에서 더 늦게 사용
2. Internal State Drift
1. 정의
- 메모리 셀 cj의 입력이 주로 양수 또는 음수일 경우 내부 상태 sj가 시간이 지남에 따라 점점 멀리 이동
- 이에 따라 $h'(s_{j})$의 값이 작아져서 그라디언트가 사라질 수 있다.
2. Solution
1. 입력 게이트 초기 바이어스 조정
2. 로지스틱 시그모이드 활성화 함수
3. 적절한 h 함수 선택
5. Experiement
1. 서론
1. long time lag problem(긴 시간 지연 문제)
- 입력 데이터와 출력 데이터 사이의 시간 간격이 매우 길 경우, 그 사이의 의존성을 학습하기 어려워지는 현상
2. 목표
- LSTM이 기존의 제시된 방법보다 더 우수한 성능임을 입증
- RTRL, BPTT 등 기존의 제시된 방법은 긴 시간 지연 문제에서 오차가 지수적으로 감소하는 현상으로 인해 제대로 작동하지 않는다.
3. 문제 설정
1. 학습 데이터셋에 긴 시간 지연 사례만 포함
2. 과제가 단순한 무작위 가중치 추측과 같은 단순한 알고리즘으로는 빠르게 해결되지 않을 만큼 충분히 복잡
- 무작위 가중치 추측같은 단순한 알고리즘으로는 해결되지 않을만큼
4. 실험 설계
1. 온라인 학습 및 로지스틱 시그모이드 사용
2. 실험 1과 2에서는 초기 가중치를 [−0.2, 0.2] 범위에서 선택하고, 나머지 실험에서는 [−0.1, 0.1] 범위에서 선택
3. 실험 데이터는 과제에 따라 무작위 생성
4. 학습 과정은 메모리 셀과 게이트 구조를 포함한 LSTM 기반 구조에서 이루어진다.
5.1. 실험 1: 임베디드 Reber 문법
1. Reber grammer
- Reber 문법을 학습하는 것은 순차적인 데이터를 처리하는 능력을 평가하는 것이며, 각 기호가 어떤 규칙을 따르는지 모델이 학습하도록 하는 것
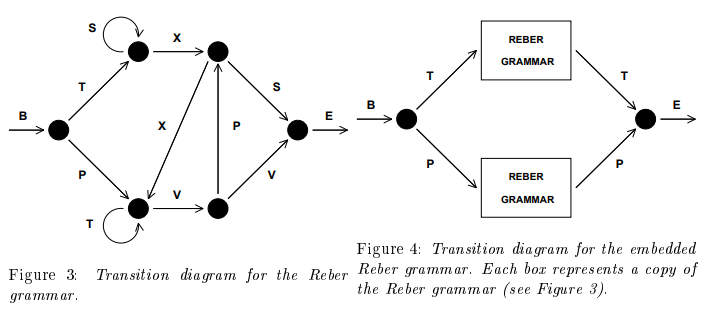
- 짧은 시간 지연 문제를 포함하는 경계 사례입니다.
- 이 실험은 LSTM의 출력 게이트가 기억을 보호하고 불필요한 신호를 차단하는데 중요한 역할을 한다는 것을 입증
- 기존 알고리즘(BPTT, RTRL)도 학습이 가능하지만 LSTM이 더 우수한 성능을 보입니다.

5.2. 실험 2: 노이즈 없는 시퀀스와 노이즈가 포함된 시퀀스
- 최종 요소를 예측하기 위해 네트워크는 첫 번째 요소를 p 타임 스텝 동안 저장해야 한다.
1. Task 2a : 긴 시간 지연이 있는 노이즈 없는 시퀀스
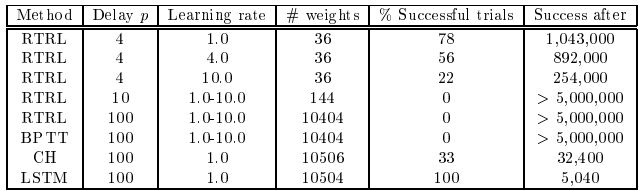
- 기존 RTRL과 BPTT는 시간 지연이 길어질수록 실패
- 반면 LSTM은 메모리 셀과 입력 게이트를 사용하여 첫 번째 입력을 성공적으로 저장하고, 최종 출력에 반영
2. Task 2b : 지역적 규칙이 없는 경우 - 입력 시퀀스의 압축 가능성을 제거하면 일반적인 신경망 구조는 실패하지만, LSTM은 이 경우에도 높은 성능을 유지
3. Task 2c : 매우 긴 시간 지연 및 규칙성 없는 작업
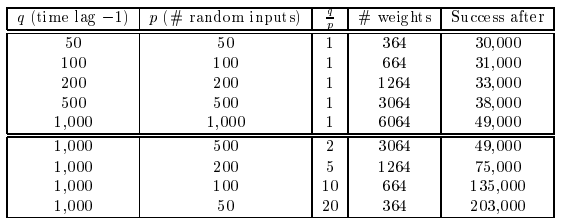
- 방해 기호가 포함된 잡음 있는 환경에서 테스트합니다.
- 최소 시간 지연이 길어질수록 기존 알고리즘은 실패하지만, LSTM은 이를 해결합니다.
5.3. 실험 3: 동일 입력 라인의 신호와 잡음
1. Task 3a
- 문제 자체가 단순하여, 무작위 가중치 추정(random weight guessing) 방식도 쉽게 해결할 수 있으나, 이는 성능을 테스트 하는 것이 아닌 LSTM이 신호와 노이즈를 구별할 수 있음을 확인하는데 사용된다.
- 즉, 신호와 노이즈가 혼합된 데이터를 처리하는데 문제가 있는 것을 테스트하기 위한 기반 문제라고 생각하면 된다.

- ST1: 임의로 선택된 테스트 세트(256개 시퀀스)에서 오분류가 없는 경우
- ST2: ST1을 충족하고 평균 절대 테스트 오류가 0.01 미만인 경우.
2. Task 3b
- Task 3a와 동일하지만, 이제 관련 정보를 포함한 첫 N개의 시퀀스 요소에도 평균 0, 분산 0.2의 가우시안 노이즈를 추가
- 노이즈를 추가했음에도 문제를 해결했다는 것은 LSTM이 노이즈를 무시하고 중요한 정보를 학습하는 데 강력한 알고리즘임을 보여준다.
- 기존 문제와 더 어려운 변형 문제를 포함합니다.
- LSTM은 복잡한 조건부 기대값을 학습할 수 있습니다.

- ST1: 임의로 선택된 테스트 세트(256개 시퀀스)에서 오분류가 6개 미만인 경우
- ST2: ST1을 충족하고 평균 절대 테스트 오류가 0.04 미만인 경우
3. Task 3c
- 클래스 1은 0.2, 클래스 2는 0.8이며, 가우시안 노이즈(평균 0, 분산 0.1, 표준편차 0.32)가 추가

5.4. 실험 4 : 더하기 문제 (Adding Problem)
- 이 실험은 분산되고 연속적인 값으로 이루어진 표현을 처리하는 LSTM 시험
1. 실험 방식
1. X1, X2를 실수, 마커의 규칙에 따라 선정
2. 0.5 + (X1 + X2 / 4.0)으로 타깃값 선정
3. ±0.04 범위 내에 있으면 정답으로 간주
2. 결론
- 이 실험은 LSTM이 단순히 패턴을 학습하는 것이 아니라, 연속 값 기반의 산술 연산을 수행할 수 있음을 입증
- 표시된 마커에 따라 필요한 값을 정확히 기억하고 합산하는 능력을 보여준다.
5.5. 실험 5 : 곱셈 문제 (Multiplication Problem)
- LSTM이 비통합적(non-integrative) 해결 방법이 요구되는 과제를 해결할 수 있는지를 조사
1. 실험 방식
1. 이전 섹션 5.4의 더하기 문제와 유사하지만, 첫 번째 구성요소 값의 범위가 [0,1]로 제한
2. 시퀀스 끝에서 타깃 값은 표시된 두 값의 곱 X1 * X2로 설정
3. 첫 번째 입력 쌍이 표시되는 드문 경우에는 X1=1.0로 설정
- 분산된 입력과 긴 시간 지연을 포함하는 과제입니다.
- 단순히 값을 저장하고 더하는 것이 아닌 두 값의 관계를 이해 및 기억 해야 하며 시퀀스에 따라 정밀도를 요구한다.
- 기존 알고리즘으로는 해결 불가능하지만 LSTM은 가능합니다.
5.6. 실험 6: 복잡한 시간 순서 정보 추출
- 시간적 순서를 학습해야 하는 문제입니다.
- LSTM은 멀리 떨어진 입력 신호의 순서를 효과적으로 학습합니다.
6. Discussion
1. Limitations of LSTM
1. LSTM의 한계
- 입력들이 매우 먼 시간 간격에 위치하고 그 사이에 노이즈가 섞인 시퀀스가 주어지는 문제입니다. 이런 문제는 LSTM이 잘 처리하지 못하는 경우가 많습니다. 이유는 특정 입력을 저장하는 것만으로는 전체 문제를 해결할 수 없기 때문
2. 추가적인 유닛 필요
- 각 메모리 셀 블록은 두 개의 추가 유닛(입력 게이트와 출력 게이트)을 필요로 한다.
3. 피드포워드 네트워크와 유사한 문제
1. 패리티 문제 (Parity Problem)
- 비트 시퀀스에서 1의 개수가 짝수인지 또는 홀수인지를 판별하는 문제입니다.
- LSTM의 구조적 장점(게이트 메커니즘)이 있음에도 불구하고, 500단계 이상의 입력을 정확히 처리하려면 충분히 훈련되지 않은 경우 기울기 소멸이나 학습 실패가 발생할 수 있다.
- 모든 정보를 기억하고 연산하는데는 아직 취약하다.
4. 최근성 문제
- 최근성 문제란, 특정 시점에서 입력의 "시간적 중요성"을 다룰 때 발생하는 문제로 시간 간격이 매우 미세하게 구별되어야 하는 경우에는 추가적인 메커니즘이 필요할 수 있다.
- LSTM이 본질적으로 장기 의존성 문제를 해결하도록 설계되었지만, 모든 시간 기반 문제를 완벽히 처리할 수는 없음을 보여준다.
2. Advantages of LSTM
1. 긴 시간 지연 문제 해결 능력
2. 긴 시간 지연과 노이즈 처리
3. 일반화되는 성능
4. 파라미터 튜닝의 필요 없음
- LSTM은 학습률, 입력 게이트 편향 및 출력 게이트 편향과 같은 다양한 파라미터에 대해 잘 작동
5. 업데이트 복잡도
- LSTM 알고리즘의 가중치 및 시간 단계별 업데이트 복잡도는 기본적으로 BPTT와 동일하며, O(1)
7. Conclusion
1. CEC(상수 오류 회전 장치)를 통한 지속적인 오류 흐름 보장
- CEC는 LSTM의 핵심 구성 요소로, CEC는 오류 신호를 메모리 셀 내부에서 계속 순환시키는 역할을 하며, 이 과정에서 입력 게이트와 출력 게이트를 통해 유지 및 변환
2. LSTM의 응용
1. 시계열 예측(실험 4, 5)
2. 음성 처리