[2025-1] 차승우-GloVe: Global Vectors for Word Representation
https://aclanthology.org/D14-1162.pdf
0. Abstract
최근 단어의 벡터 공간 표현을 학습하는 방법은 CBOW, skip - gram 등의 방식을 통한 벡터 연사을 통해 의미적, 문법적 규칙성을 포착하는데 성공했지만, 이런한 규칙성이 발생하는 근원은 명확하지 않다.
본 논문에서는 이러한 규칙성이 나타나기 위해 필요한 모델 특성을 분석하고 명확히 한다. 그 결과로써 기존 문헌의 두 주요 모델 계열(전역 행렬 분해(LSA) 및 지역 문맥 창(Bag-of-words, skip-gram))의 장점을 결합한 새로운 전역 로그-선형 회귀 모델을 제안한다.
단어 유추(word analogy) 과제에서 75%의 성과를 보였으며, 유사성 비교 및 개체명 인식에서 기존 모델 대비 우수한 성과를 거두었다.
1. Introduction
단어 벡터를 학습하는 두가지 모델 계열은 다음과 같다.
1. 전역 행렬 분해(global matrix factorization) 방법: 잠재 의미 분석(LSA, Latent Semantic Analysis) (Deerwester et al., 1990)
2. 지역 문맥 창(local context window) 방법: Mikolov et al. (2013c)의 skip-gram 모델
LSA 의 경우 통계적 방식, 문서 전체에 각 단어의 빈도수를 통한 통계적 정보를 활용하지만, 단어 유추 과제에서 성능이 낮아 벡터 공간 구조가 최적이 아니다. 예를 들면, king − queen = man − woman 에서 king − queen = man − ? 이런 방식으로 제시가 되었을 때, women이라는 관계를 잘 유추하지 못한다는 것이다.
반면 skip-gram 같은 모델은 중심 단어의 주변 단어를 통해 의미적, 구문적 관계를 유추하고 손실 함수를 통해 학습하여 관계성을 명확히 하는 방식의 모델인데, 여기서 window라는 개념을 사용하기 때문에 임베딩 벡터가 LSA와 달리 전체적인 정보를 반영하지 못하고 window에 한정하는 정보를 반영하지 못하는 문제점이 존재한다.
그렇기에 본 논문에서는 의미적, 구문적 관계를 유추하기 위해 로그-선형 모델을 적합하다고 주장하며, 통계 정보를 효율적으로 활용하기 위해 global word-word co-occurrence counts(전역 단어-단어 공출현 횟수)를 학습 데이터로 사용하는 weighted least squares(가중 최소 제곱) 모델을 제안한다.
2. Related work
위에서 간단하게 살펴보았듯이 단어 벡터를 학습하는 두가지 모델 계열이 있다.
먼저 행렬 분해 방식은 코퍼스의 전체적인 통계 정보를 통해 나타는 행렬을 차원 축소를 통해 근사 분해하는 방식으로 LSA, HAL 같은 방식이 존재한다.
HAL과 유사한 방법(행렬 분해 방식)의 주요 문제는 가장 자주 등장하는 단어(예: "the", "and")가 유사성 측정에 과도한 영향을 준다는 점이다. 이는 의미적 관련성을 잘 반영하지 못한다.
이를 해결하기 위하여, COALS(Rohde et al., 2006)는 공출현 행렬에 엔트로피나 상관 기반 정규화를 적용한다. 이 정규화는 공출현 빈도 범위를 압축하여 데이터가 더 균일하게 분포되도록 한다.
다음으로는 local context windows(지역 문맥 창) 내에서 예측을 돕는 단어 표현을 학습하는 방식으로 skip - gram, CBOW 모델이 제안 되었으나, 코퍼스의 공출현 통계를 직접 다루지 않는다는 단점이 있다. 그렇기에 공출현 통계의 반복적 특성을 제대로 활용하지 못한다.
3. GloVe model
3.1. 윈도우 기반 동시 등장 행렬(Window based Co-occurrence Matrix)
단어의 동시 등장 행렬은 행과 열을 전체 단어 집합의 단어들로 구성하고, i 단어의 윈도우 크기(Window Size) 내에서 k 단어가 등장한 횟수를 i행 k열에 기재한 행렬을 말합니다.
아래와 같은 3개 문서로 구성된 텍스트 데이터가 있다고 해봅시다.
I like deep learning
I like NLP
I enjoy flying

윈도우 크기가 N일 때는 좌, 우에 존재하는 N개의 단어만 참고하게 됩니다. 윈도우 크기가 1일 때, 위의 텍스트를 가지고 구성한 동시 등장 행렬은 다음과 같습니다.
위 행렬은 행렬을 전치(Transpose)해도 동일한 행렬이 된다는 특징이 있습니다. 그 이유는 i 단어의 윈도우 크기 내에서 k 단어가 등장한 빈도는 반대로 k 단어의 윈도우 크기 내에서 i 단어가 등장한 빈도와 동일하기 때문입니다.
3.2. 동시 등장 확률(Co-occurrence Probability)
동시 등장 확률 P(k | i)는 동시 등장 행렬로부터 특정 단어 i의 전체 등장 횟수를 카운트하고, 특정 단어 i가 등장했을 때 어떤 단어 k가 등장한 횟수를 카운트하여 계산한 조건부 확률입니다.
P(k | i)에서 i를 중심 단어(Center Word), k를 주변 단어(Context Word)라고 했을 때, 위에서 배운 동시 등장 행렬에서 중심 단어 i의 행의 모든 값을 더한 값을 분모로 하고 i행 k열의 값을 분자로 한 값이라고 볼 수 있겠습니다. 다음은 GloVe의 제안 논문에서 가져온 동시 등장 확률을 표로 정리한 하나의 예입니다.


표를 보면 보이다시피, 중심단어와 연관있는 주변 단어의 경우 동시 등장 확률이 크고 이와 달리 연관이 적은 경우는 작은 것을 알 수 있다. 또한 크기 관계 비를 보자면, 중심 단어와 관련 있는 단어와 관련 없는 단어를 크기 관계 비를 통해 나타내면, 비율이 확연히 크다는 것을 알 수 있다.
예시를 들자면, ce가 등장했을 때 solid가 등장할 확률 0.00019은 steam이 등장했을 때 solid가 등장할 확률인 0.000022보다 약 8.9배 크다. 그도 그럴 것이 solid는 '단단한'이라는 의미를 가졌으니까 '증기'라는 의미를 가지는 steam보다는 당연히 '얼음'이라는 의미를 가지는 ice라는 단어와 더 자주 등장할 것이다.
수식적으로 다시 정리하여 언급하면 k가 solid일 때, P(solid l ice) / P(solid l steam)를 계산한 값은 8.9가 나온다.. 이 값은 1보다는 매우 큰 값입니다. 왜냐면 P(solid | ice)의 값은 크고, P(solid | steam)의 값은 작기 때문이다.
크기 비율이 1인 경우는 동시에 비교하는 두 단어가 비슷한 빈도로 등장하기 때문에 1에 가까운 값이 나온다고 보면 된다.
우리는 동시 등장 행렬과 동시 등장 확률의 이해를 바탕으로 손실 함수를 설계한다.
3.3. GloVe의 목표
GloVe 모델의 개요는 단어 표현을 학습할시, 통계에서 의미가 어떻게 생성되는지, 결과 단어 벡터가 그 의미를 어떻게 나타내는지에 대한 질문을 탐구하고 새로운 단어 표현 모델인 GloVe를 제안하는 것이다.
즉, 임베딩 된 중심 단어와 주변 단어의 관계, 내적이 최대한 위에서 나온 동시등장확률이 되도록 하는 것을 찾는 것이 목표라고 보면 된다.
3.5. Glove model 분석
1. 공출현 확률과 공출현 확률의 비율
- 3.2 에서 언급했다시피, Co-occurrence Probability(동시 출현 확률)은 의미적 차이를 잘 구별하나, CBOW, skip-gram의 방식과 달리 단어 간의 상대적 관계를 표현하기에는 적합하지 않습니다. 그렇기에GloVe model에서는 확률의 비율을 사용하여, 단어 간의 관계의 상대적, 구문적 관계를 잘 표현할 수 있기 때문에 GloVe에서는 공출현 확률의 비율을 통해 나타냅니다.
이 목적에 따라 식을 표현하면 다음과 같다.
$$dot\,product\,P(K | i) = P_{ik}$$
공출현 확률로는 관계를 파악하기 모자르기 때문에 공출현 확률의 비율을 적용하여
$$F(w_{i},w_{j},\widetilde{w_{k}})\,=\,\frac{P_{ik}}{P_{jk}}$$
라는 초기 식으로 전개를 시작합니다.
두 개의 중심단어, 하나의 주변 단어를 사용하는 이유는 두 중심 단어가 동일한 주변 단어에 대해 맺는 관계를 비교하면, 의미적 대조와 상대적 차이를 더 명확히 파악할 수 있습니다. 하나의 주변 단어 wk를 고정하면, 두 중심 단어의 관계를 모델링하는 데 초점을 맞출 수 있습니다.
먼저 두 단어의 동시 등작 확률의 크기 관계 비를 나타내는 것이 목적이기에 wi, wj 두 벡터의 차리를 입력으로 사용합니다.
위 식을 나타내면
$$F(w_{i}-w_{j},\,\widetilde{w_{k}}) = \frac{P_{ik}}{P_{jk}}$$
로 나타낼 수 있고 두 값의 관계를 나타내기 위해 내적을 사용하여 관계를 나타내줍니다.
$$F(w_{i}-w_{j},\,\widetilde{w_{k}}) = \frac{P_{ik}}{P_{jk}}$$
단어와 문맥 사이의 역할은 교환될 수 있으므로, 즉, w와 ~w를 교환했을때도 모델은 동일하게 작동해야 한다. 이를 만족하기 위해서는 함수 F는 실수의 덥셈과 양수의 곱셈에 대해서 준동형(Homomorphism)을 만족하도록 합니다. 즉, F(a + b) = F(a)F(b)를 만족시켜야 합니다.
F(a + b) = F(a)F(b) 에서 a와 b가 각각 사실 두 벡터의 내적값이라고 하면 결과값으로 스칼라 값이 나올 수 있다. 그러므로 아래와 같이 나타낼 수 있다.
$$F(v1^{T}v2 + v3^{T}v4)\,=\, F(v1^{T}v2)F(v3^{T}v4)$$
위의 준동식을 GloVe에 적용시키기 위해 뺄셈에 대한 식으로 변경하게 된다면, 아래와 같이 나타낼 수 있다.
$$F(v1^{T}v2 + v3^{T}v4)\,=\,\frac{F(v1^{T}v2)}{F(v3^{T}v4)}$$
해당 식을 $F(w_{i}-w_{j},\,\widetilde{w_{k}}) = \frac{P_{ik}}{P_{jk}}$ 에 적용 시키게 된다면 아래와 같이 나타낼 수 있다.
$$F(w_{i}-w_{j}^{T}w_{k})\,=\,\frac{F(w_{i}^Tw_{k})}{F(w_{j}^{k}w_{k})}$$
$$F(w_{i}-w_{j},\,\widetilde{w_{k}}) = \frac{P_{ik}}{P_{jk}}$$
이런 F를 만족시킬 수 있는 함수가 존재하는데, 이는 지수 함수를 통해 가능하다. 지수함수를 통해 나타낸다면,
$$exp((w_{i}-w_{j})^{T}w_{k})\,=\,\frac{exp(w_{i}^{T}w_{k})}{exp(w_{j}^{T}w_{k})}$$
$$exp(w_{i}^{T}w_{k})\,=\,P_{ik}\,=\,\frac{X_{ik}}{X_{i}}$$
위 식은 아래와 같이 나타낼 수 있다.
$$w_{i}^{T}w_{k}\,=\,logP_{ik}\,=\,log(\frac{X_{ik}}{X_{i}})\,=\,logX_{ik}-logX_{i}$$
여기서의 문제는 i와 k의 관계를 바꿔어도 같아야 하는데, log xi가 걸리기 때문에 이를 편향 bi로 취급하여 대체합니다. 이와 같게 i와 k의 관계를 바꾸어도 유지해야 하기 때문에, 편향 bk 또한 추가로 해서 식을 나타내면
$$w_{i}^{T}w_{k}+b_{i}+b_{k} = logX_{ik}$$
로 나타낼 수 있고, 좌변을 학습하는 식, 우변을 정답으로 보면 Loss 함수를 다음과 같이 나타낼 수 있다.
$$L=\sum_{m,n=1}^{V}(w_{m}^{T}\widetilde{w_{n}}+b_{m}+\widetilde{b_{n}}-logX_{mn})^{2}$$
$log(X_{ik})에서 X_{ik}=0$일 경우 로그가 발산하는 문제를 방지하기 위해 1을 더하여 X의 희소성을 유지하며 발산 문제를 해결하였다.
$$log(X_{ik})\,\to\,log(1+X_{ik})$$
여기에 드문 공출현(희소 데이터)이 과도한 영향을 미치지 않도록 하기 위해, 가중치를 추가한 비용함수를 추가해서 아래와 같이 나타난다.
$$J=\sum_{m,n=1}^{V}f(X_{mn})(w_{m}^{T}\widetilde{w_{n}}+b_{m}+\widetilde{b_{n}}-logX_{mn})^{2}$$
가중치 함수 f는 드문 공출현이 과도하게 높은 가중치를 받지 않도록 비감소 함수여야 하며 또한 빈번한 공출현에 대해서는 과도하게 높은 가중치를 받지 않도록 해야 하기 때문에 다음의 식이 제안된다.

$$f(x)=min(1,(x/x_{max}^a))$$
a의 경우 실행을 통해 3/4에서 좋은 성능을 보여준다.
4. Experiment & Result
4.1. Experiement
1. Word Analogy(단어 유추 과제)
1. 의미론적 질문(Semantic subset)
2. 구문론적 질문( Syntactic subset)
2. Word Similarity (단어 유사성)
3. 하이퍼 파라미터
- Adagrad, $X_{max}=100$, a = 3/4, learning rate = 0.05
4.2. Result
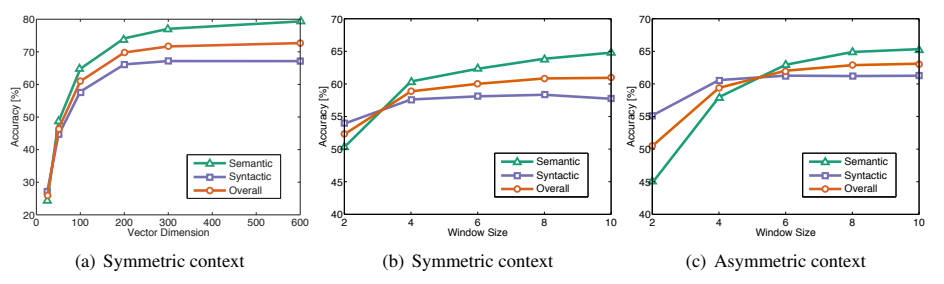
1. Vector size
- 200차원 이상에서는 성능 개선이 점차 둔화.
2. Window size
1. symmetric(대칭)
- 목표 단어의 왼쪽과 오른쪽으로 확장된 문맥 창.
2. asymmetric(비대칭)
- 목표 단어의 왼쪽으로만 확장된 문맥 창.

1. Semantic(구문적 표현)
- 말뭉치 크기가 증가함에 따라 성능이 단조롭게 증가
2. Syntactic(의미적 표현)
- Wikipedia 말뭉치로 학습한 모델이 더 큰 Gigaword 말뭉치로 학습한 모델보다 더 나은 성능
- Wikipedia는 이와 관련된 지역 정보를 포괄적으로 다루는 반면, Gigaword는 그렇지 않음
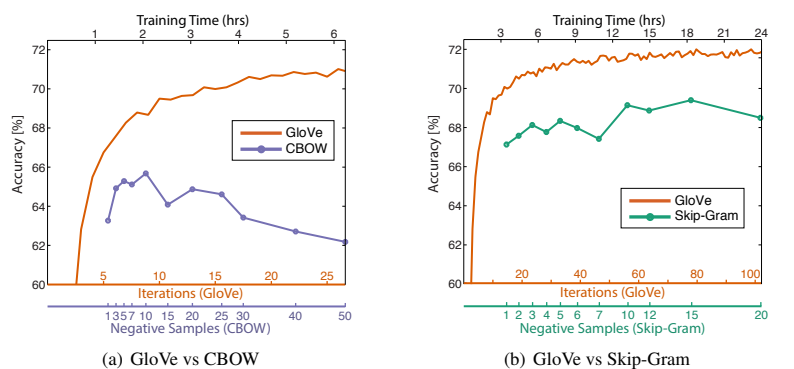
1. 동일한 말뭉치, 어휘, 문맥 창 크기, 훈련 시간에서 항상 word2vec보다 우수.
2. Word2Vec의 경우 부정 샘플링이 목표 확률 분포를 제대로 근사하지 못하기 때문으로 추정되어 부정 샘플 수가 약 10을 초과하면 성능이 감소.
5. Conclusion
1. 단어의 분포 기반 표현을 학습하는 방법에서 카운트 기반 방식과 예측 기반 방식 중 어느 것이 우수한지에 대한 논의
2. 두 가지 모델 모두 장점이 있기에 카운트 데이터의 이전을 활용하여 로그-선형모델을 통해 모델 설계
3. GloVe, 단어 유추, 유사성 등에 있어 기존 모델에 대비 우수한 성능을 가지게 됨